我们可以从黑盒模型中学到什么

使用非线性模型进行数据探索和知识生成

黑盒模型可以自动模拟复杂的关系。与线性模型相比，捕捉数据中的这些趋势可以提高其准确性。

然而，准确性只是好处之一。

我们可以分析模型，了解它们如何做出这些预测。这可以揭示数据集中的潜在关系。在某些情况下，这些关系对我们来说可能是全新的。这就是机器学习如何成为数据探索和知识生成的工具。

此外，提供感知检查以帮助调试模型。这些知识可用于

• 为非线性模型提供特征工程信息。
• 在做出超越模型的决策时提供帮助。

我们将讨论如何从黑盒模型中学习。其中包括理解数据中的重要关系及其性质。

为什么我们可以从非线性模型中学习？

在深入探讨之前，让我们先讨论一下为什么我们可以从这些模型中学习。非线性模型可以模拟我们数据中的非线性关系和相互作用。例如，以图 1 中的二手车价格散点图为例。汽车价格(price)并不总是随着车龄(age)的增加而下降。对于经典汽车（classic = 1），价格会增加。我们说我们的数据中存在相互作用。价格和车龄之间的关系取决于第三个特征——classic。

非线性模型可以自动模拟此类关系。让我们以图 2 中的简单决策树为例。首先将汽车分为普通 (0) 和经典 (1)。对于普通汽车，如果汽车车龄不到 15 年，则价格较高。对于经典汽车，价格较低。这并不能完全捕捉我们在图 1 中看到的关系。为此，我们可以向决策树添加更多层。我们还可以使用更复杂的算法，如随机森林、XGBoost 或神经网络。

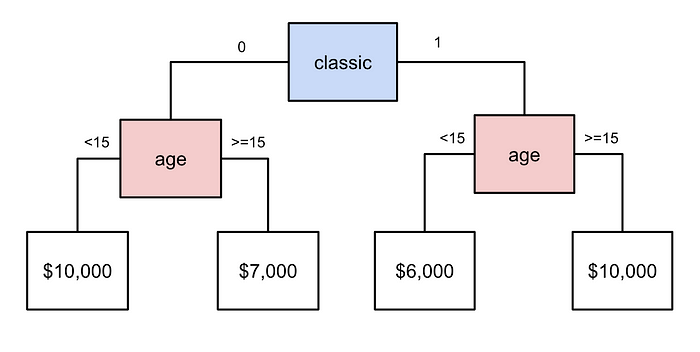
当我们谈论数据探索/知识生成时，我们通常会依赖这些更复杂的算法。它们有时被称为可解释模型或黑盒模型。它们能够捕捉数据中的复杂关系。同时，我们不需要“告诉”它们这些关系存在。就像决策树一样，我们可以只给它们经典和年龄特征。模型会在进行预测时自动利用特征之间的相互作用。

相比之下，线性模型（即线性和逻辑回归）不太复杂。要用这些模型捕捉非线性关系，我们需要进行特征工程。使用新特征，我们可以将非线性关系表示为线性关系。要了解要创建什么特征，我们需要探索我们的数据。我们可能还需要相关领域的领域知识。

从某种意义上说，黑盒模型在模型结构内进行特征工程。它们非常擅长在数据中发现模式。问题是模型的内部工作原理太复杂了。我们无法仅通过查看模型参数/结构来了解它们如何进行预测。我们需要使用其他技术来了解它们的工作原理。

我们能学到什么？如何学到？

这就是可解释机器学习 (IML) 领域的用武之地。除其他外，它旨在开发我们可以用来理解黑盒模型如何进行预测的方法。我们讨论其中一些技术以及它们可以教给我们关于模型/数据的知识。

提供基准

首先，黑盒模型可以提供的一个有价值的信息是基准。通过捕捉非线性关系和相互作用，这些模型可以提高预测的准确性。要确定性能，我们实际上并不需要 IML 方法。我们可以依靠准确率、精确率或召回率等指标或 ROC 曲线等可视化。

使用黑盒模型可以告诉我们我们能够多好地预测目标变量。我们可以将这些结果与不太复杂的线性模型的性能进行比较。假设我们发现黑盒模型明显更准确。这告诉我们线性模型缺少我们数据中的重要关系。此时，我们可以使用 IML 方法来了解这些关系是什么。

重要关系

首先，我们可以了解数据中的哪些特征是重要的。这些特征可用于预测目标变量。大多数非线性模型能够处理大量特征（超过 50 个）。这些特征是否高度相关也没关系。这意味着，通过使用非线性模型，我们可以了解大量特征的重要性。相比之下，线性回归等模型需要一组较小的（8-10 个）不相关的特征。

我们可以使用的一个度量是排列特征重要性。在图 3 中，您可以看到用于预测鲍鱼年龄的 xgboost 模型的得分。我们可以看到，鲍鱼壳的长度在预测年龄时很重要。接下来的三个特征基于鲍鱼的重量。虽然这些特征高度相关，但它们对模型没有负面影响。我们可以理解，所有这些特征都可以用来预测年龄。

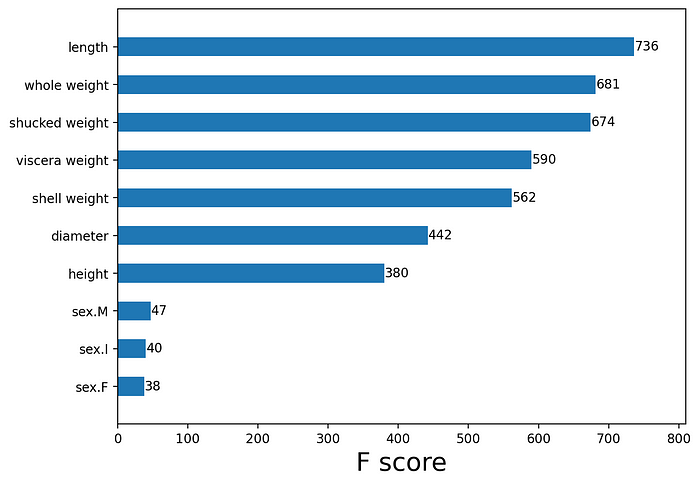
如果我们使用相关性来识别重要关系，我们可能会错过其中一些特征。这是因为相关性仅提供线性关联的度量。换句话说，该度量只能突出显示具有显着线性关系的特征。相比之下，特征重要性告诉我们特征对模型预测的重要性。模型的预测能力可能来自相互作用和非线性关系。这些将反映在特征重要性分数中。

SHAP 值可以提供另一种衡量标准。我们可以使用这些值来找到每个特征的绝对平均 [[SHAP 值]]。与特征重要性类似，这可以说明哪些特征对预测做出了巨大贡献。这两个衡量标准的问题是，它们没有告诉我们模型捕获的关系的性质。

非线性关系

如果特征与目标变量有任何关系，则可以使用该特征进行预测。它可以是线性的，也可以是图 4 中所示的非线性关系之一。为了找到并可视化黑盒模型捕获的非线性关系，我们可以使用其他 IML 方法。

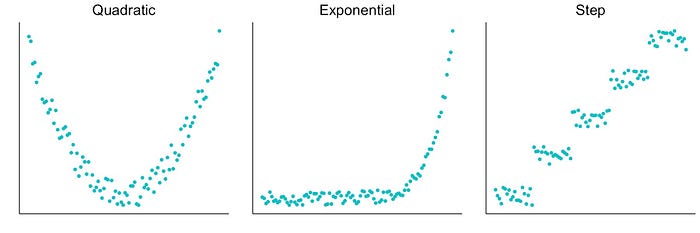
可视化的示例包括部分依赖图(PDP)和累积局部效应(ALE) 图。这两种方法都显示了特征与模型预测之间的一般关系。PDP 易于理解，但可能会受到特征依赖性的负面影响。ALE 图没有这个问题，但它们更复杂，更难解释。

另一种方法是使用 SHAP 值。我们上面提到过这些。对于给定的预测，它们给出了每个特征对该预测的贡献。我们可以绘制 SHAP 值与特征值的关系图。这被称为依赖关系图。它可以向我们展示特征值与其对预测的贡献之间的关系。

我们一些文章中讨论这些方法和更多方法。在《[[查找并可视化非线性关系]]》中深入探讨了如何查找和可视化非线性关系。在《[[Python 中的 SHAP 简介]]》重点介绍SHAP 值和用于应用它们的 Python 代码。我们还讨论了这些值的不同聚合。其中包括上面提到的平均 SHAP 和依赖关系图。

互动

交互实际上被认为是一种非线性关系。它们相对于一个特征是非线性的。该特征的关系将取决于第三个特征的值。事实上，交互可能更加复杂。一个特征的关系可能取决于两个或多个特征的值。对于大多数应用，我们只关心两个特征之间的关系。

一种可视化交互的方法是ICE 图。您可以在图 5 中看到一个示例。这里，我们数据集中的每个观察值都用一条线表示。此数据集包含二手车销售的详细信息（例如价格、车龄和车型）。对于每个观察值，该线显示预测价格（部分 yhat）如何随车龄变化。粗体黄色是我们上面讨论的 PDP 的一个示例。它给出了所有单个预测线的平均值。

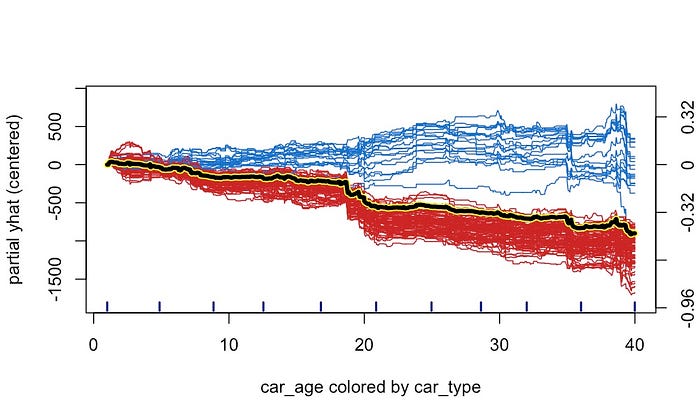
我们根据汽车类型对上面的线条进行了着色。蓝色代表经典汽车，红色代表普通汽车。您可以看到经典汽车的关系偏离了平均趋势。直观地说，经典汽车的价格会随着年龄的增长而上涨，这是有道理的。ICE 图向我们展示了汽车年龄和价格之间的关系取决于汽车的类型。换句话说，汽车年龄和汽车类型之间存在相互作用。

另一种方法是使用SHAP 交互值。这些是 SHAP 值的扩展，其中考虑了主效应和交互效应。我们可以使用这些来可视化交互。我们还可以计算平均绝对交互效应以突出显示重要的交互。这类似于特征重要性得分，但针对的是交互。用于突出显示交互的另一个指标是 Friedman 的 h 统计量。

同样，我们也在一些文章中更深入地讨论过所有这些方法。在《寻找并可视化交互》中更深入地介绍了如何查找和可视化交互。还有《[[分析与 SHAP 的相互作用]]》中重点介绍如何使用SHAP 分析交互。我们还讨论了用于应用此方法的 Python 代码。

我们可以用这些知识做什么？

所有这些 IML 方法都可以帮助我们了解模型如何进行预测。一个直接的好处是它们可以帮助我们感知检查我们的模型。我们可以将模型捕获的关系与我们使用领域知识所预期的关系进行比较。这些方法还使我们能够向客户或同事解释我们的模型。

在本节中，我们将集中讨论间接好处。通过理解模型，我们可以了解数据中的潜在关系。我们可以利用这些知识来改进线性模型或实现超越模型的决策。

改进线性模型

我们提到，黑盒模型可以提供基准。它们可能优于线性模型，但这并不意味着这些模型的终结。这是因为我们可以利用所获得的知识来指导我们的特征工程。我们可以创建新的特征来提高线性模型的性能。

例如，假设我们想使用线性回归对二手车的价格进行建模。使用 PDP，我们发现价格与汽车年龄呈二次关系。同样，使用 ICE 图，我们发现汽车年龄和汽车类型之间存在相互作用。我们可以通过向数据集添加新特征来捕获这些非线性关系。

具体来说，在下面的等式中，我们添加了 \(age^2\) 和交互项 \(age*classic\)​。其中 classic = 1 表示经典汽车，否则为 0。 \[ \begin{align*} & \gamma = \beta_0 + \beta_1(age) + \beta_2(age^2) + \beta_3(age*classic) + \beta_4(classic) \\ & \gamma = \beta_0 + \beta_1(age) + \beta_2(age\_sqrd) + \beta_3(age\_classic\_int) + \beta_4(classic) \end{align*} \] 在第一个方程中，Y 由两个特征（age 和 classic）的非线性方程建模。现在，它由四个特征的线性方程建模。特征工程甚至可以帮助决策树等简单的非线性模型。最终，它使我们能够使用简单的模型捕获复杂的关系。我们曾在文章《特征工程的力量》中更实际地演示此过程。

问题是我们为什么要这样做？非线性模型同样准确。那么为什么不使用它们并避免额外特征工程的麻烦呢？这是因为拥有一个简单的模型有很多好处。首先，在许多行业中，对可以使用的模型类型有规定。也就是说，在银行和保险等行业中，您可能需要使用线性模型。

即使没有规定，您可能仍然更喜欢线性模型。黑盒模型很复杂。即使使用 IML 方法，我们也可能不能 100% 确定它们的工作原理。这可能会在投入生产时带来意外。相比之下，回归和决策树本质上是可解释的。我们可以通过直接查看它们的参数来了解它们的工作原理。这增加了它们对它们在野外行为的确定性。

实现决策

模型用于自动化决策。有了 IML，它们的影响不再仅限于这些决策。我们获得的知识可以为更广泛的组织提供决策信息。以前未知的关系可以提供巨大的价值。例如，我们探索的互动告诉我们，经典汽车的价格会随着年龄的增长而上涨。这可能为投资经典汽车的策略提供参考。

话虽如此，我们还是应该避免过于复杂的解决方案。使用数据来指导决策对数据科学家来说并不是什么新鲜事。我们有许多技术和工具可以用来帮助探索数据。它们大多数都比使用黑盒模型简单得多。缺点是它们确实需要一些指导。我们需要知道我们想在数据中找到什么。使用 IML 方法，黑盒模型可以为我们找到新的重要模式。

参考

C. Molnar, Interpretable Machine Learning (2021) https://christophm.github.io/interpretable-ml-book/shap.html

S. Masís, Interpretable Machine Learning with Python (2021)