KernelSHAP vs TreeSHAP

根据速度、复杂性和其他考虑因素比较 SHAP 近似方法

[[KernelSHAP]] 和 [[TreeSHAP]] 都用于近似 [[Shapley]] 值。TreeSHAP速度更快。缺点是它只能与基于树的算法（如[[随机森林]]和 [[xgboost]]）一起使用。另一方面，KernelSHAP 与模型无关。这意味着它可以与任何机器学习算法一起使用。我们将比较这两种近似方法。

为此，我们将进行一项实验。这将向我们展示 TreeSHAP 实际上有多快。我们还将探讨树算法的参数如何影响时间复杂度。这些包括树的数量、 深度和特征的数量。在使用 TreeSHAP 进行数据探索时，这些知识非常有用。最后，我们将讨论其他考虑因素（如特征依赖性）如何影响方法。

每次观察的时间

对于第一个实验，我们想看看这些方法计算 [[SHAP]] 值需要多少时间。我们不会介绍用于获取结果的代码，但你可以在 GitHub¹ 上找到它。总而言之，我们首先模拟回归数据。它有 10000 个样本、 10 个特征和 1 个连续目标变量。使用这些数据，我们训练一个随机森林。具体来说，该模型有 100 棵树，最大深度为 4 。

现在，我们可以使用该模型来计算 SHAP 值。我们使用 KernelSHAP 和 TreeSHAP 方法进行此操作。对于每种方法，我们计算 10、100、1000、2000、5000 和 10000 个 SHAP值。对于 每个金额， 我们记录计算所花费的时间。我们确保对每个金额重复此过程 3 次。然后，我们将平均值作为最终时间。

results = []
for n in [10,100,1000,2000,5000,10000]*3:
# Calculate SHAP Values
kernel_time = runSHAP(n=n)
tree_time = runSHAP(n=n,kernel=False)

result = [n,kernel_time,tree_time]
results.append(result)

results_1 = pd.DataFrame(results,columns = ['n','kernelSHAP','treeSHAP'])

---
Kernel 10000:  0:07:48.051865
Tree 10000:  0:00:00.747681

你可以在图 1 中看到此过程的结果。你可以看到 TreeSHAP 的速度明显更快。对于 10,000 个 SHAP 值，该方法耗时 0.74 秒 。相比之下，KernelSHAP 耗时 7 分 48.05 秒。这是 KernelSHAP 的 630 倍 。这些计算的速度取决于你的设备，但你应该会遇到类似的差异。

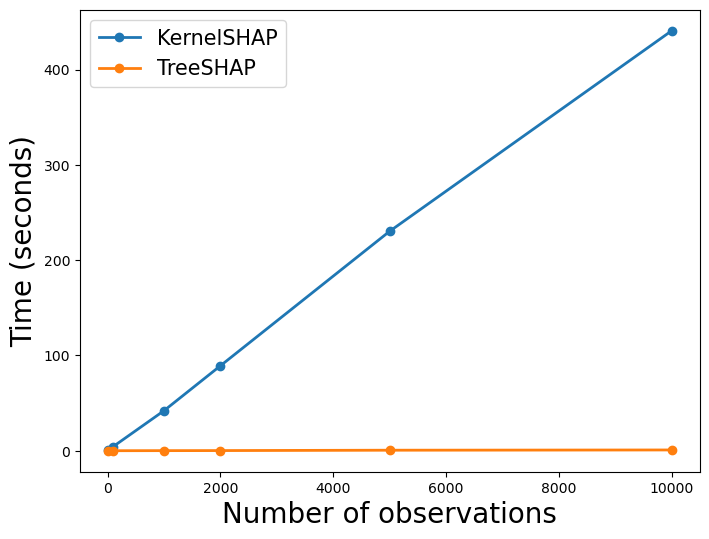
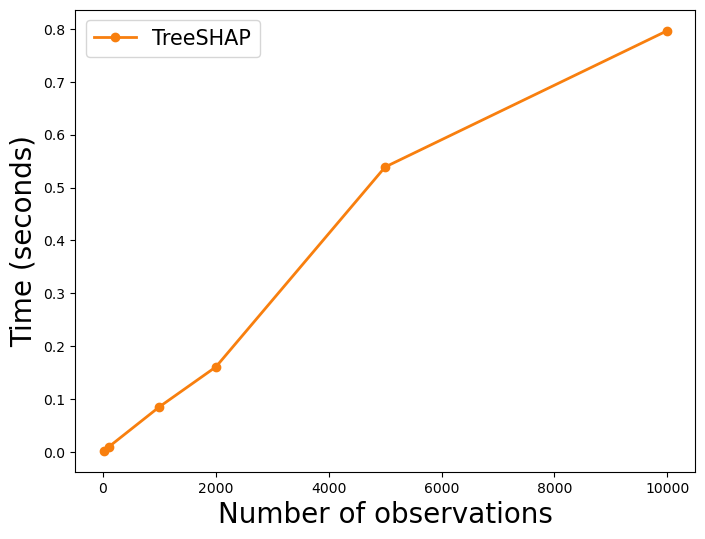
上面的 TreeSHAP 线看起来很平坦。这是因为它与 KernelSHAP 线相比显得矮小。在 图 2 中，我们只有 TreeSHAP 的线。你可以看到它也随着观察次数的增加而线性增加。这告诉我们每个 SHAP 值的计算时间都差不多。我们将在下一节探讨原因。

-

时间复杂度

两种方法的时间复杂度如下所示。这是在树算法中计算特征的 SHAP 值时的复杂度。T 是 单个树的数量。L 是 每棵树中的最大叶子数。D 是 每棵树的最大深度。最后， M 是每棵树中的最大特征数。对于这些方法，这些参数将以不同的方式影响近似时间。

\[ \begin{align*} & KernelSHAP: O(TL2^M) \\ & TreeSHAP: O(TLD^2) \end{align*} \]

只有 TreeSHAP 的复杂度受深度 (D) 的影响。另一方面，只有 KernelSHAP 受特征数量 (M) 的影响。不同之处在于 KernelSHAP 复杂度相对于 M 呈指数增长 ，而 TreeSHAP 相对于 D 呈二次增长。考虑到我们的特征 (M = 10) 也多于树深度 (D = 4)，我们可以看出为什么 KernelSHAP 更慢。

需要明确的是，这是每个 SHAP 值的时间复杂度。我们应该期望每个值都需要相似的时间来计算。这就是为什么我们看到时间与观察次数之间存在线性关系。我们现在将探讨时间与其他参数 T 、 L 、 D 和 M 之间的关系。然后我们将讨论结果对模型验证和数据探索的意义。

树的数量（T）

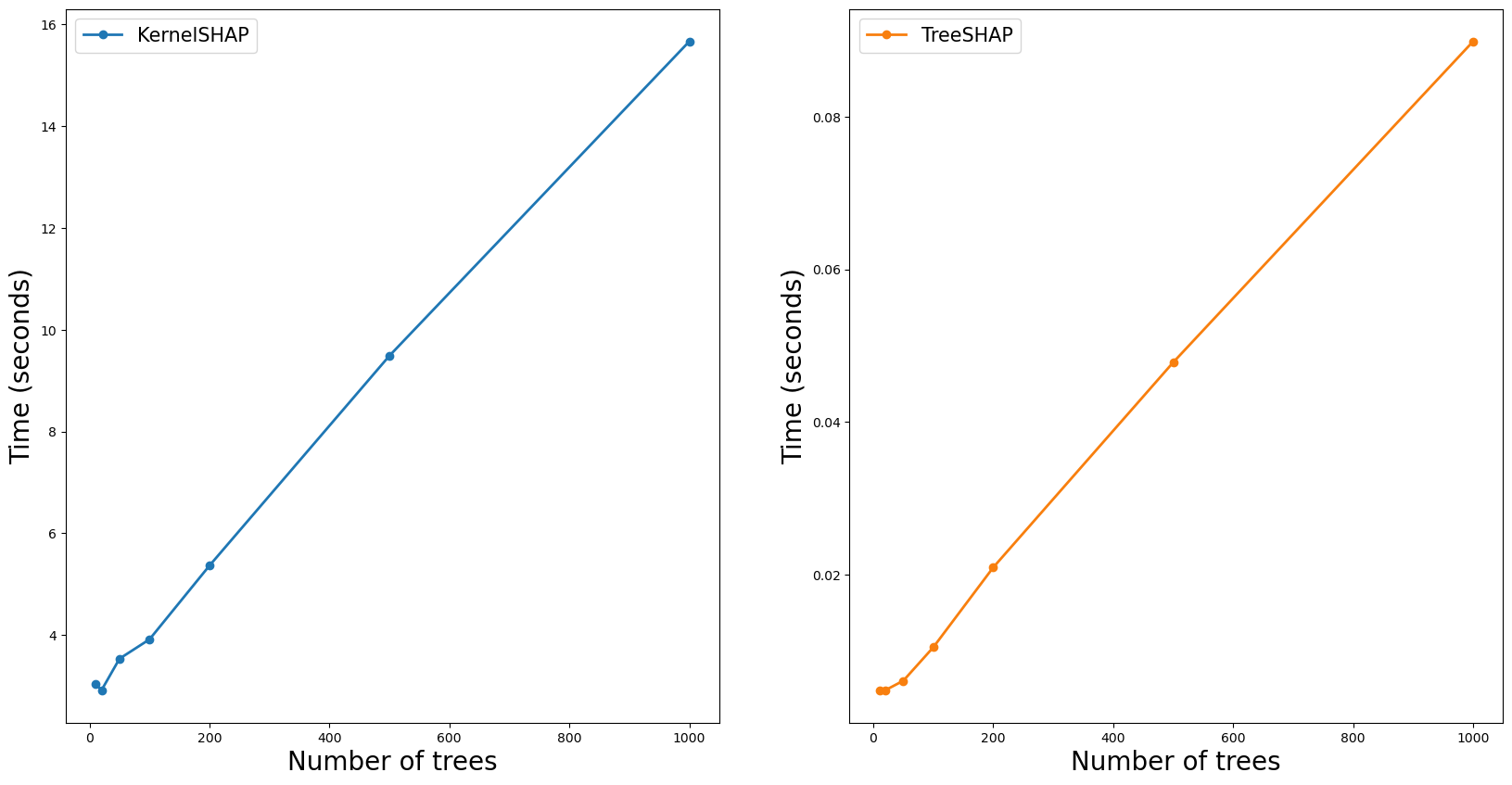
对于这两种方法，复杂度与树的数量 (T) 呈线性关系。我们预计此参数会以类似的方式影响近似时间。为了看到这一点，我们进行了与之前类似的实验。这一次，我们通过增加树的数量来训练不同的模型。我们使用每个模型来计算 100 个 SHAP 值。

你可以在图 3 中看到结果。对于这两种方法，时间都随着树的数量线性增加。这是我们在查看时间复杂度时所预期的。这告诉我们，通过限制树的数量，我们可以减少计算 SHAP 值所需的时间。

特征数量 (M)

只有 KernelSHAP 受到特征数量（ M ）的影响。这次我们在不同数量的特征上训练模型。同时，我们保持其他参数（ T、L 和 D ）不变。在 图 4 中，我们可以看到 KernelSHAP 的时间随着 M 的 增加而呈指数增加。相比之下，TreeSHAP 的时间受到的影响并不大。

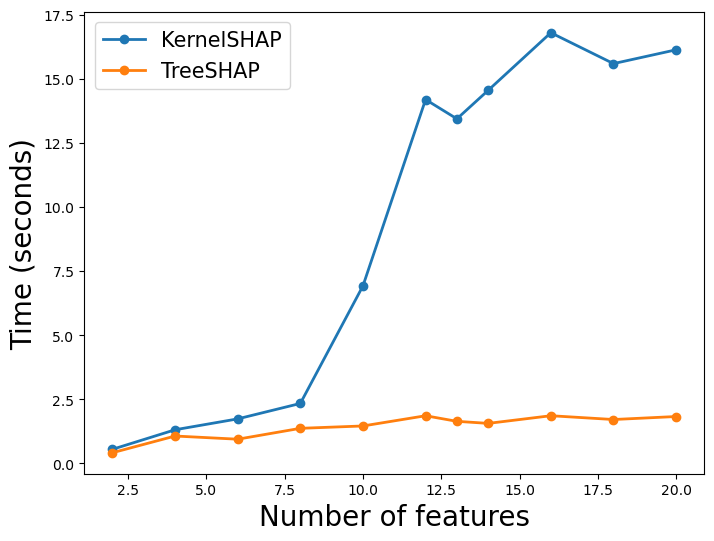
你可能已经注意到 TreeSHAP 的时间逐渐增加。这可能会令人困惑，因为我们看到复杂性并不依赖于 M。要清楚的是，这是计算单个特征的 SHAP 值时的复杂性。随着 M 的增加，我们需要为每个观察计算更多的 SHAP 值。

树的深度（D）

最后，我们改变树的深度。我们确保森林中每棵树的深度始终是最大深度。在图 5 中，你可以看到当我们增加深度时会发生什么。TreeSHAP 的时间增加得更为剧烈。甚至有一点 TreeSHAP 的计算成本快要比 KernelSHAP 还高了。我们可能已经预料到了这一点，因为我们看到只有 TreeSHAP 复杂性是 D 的函数。

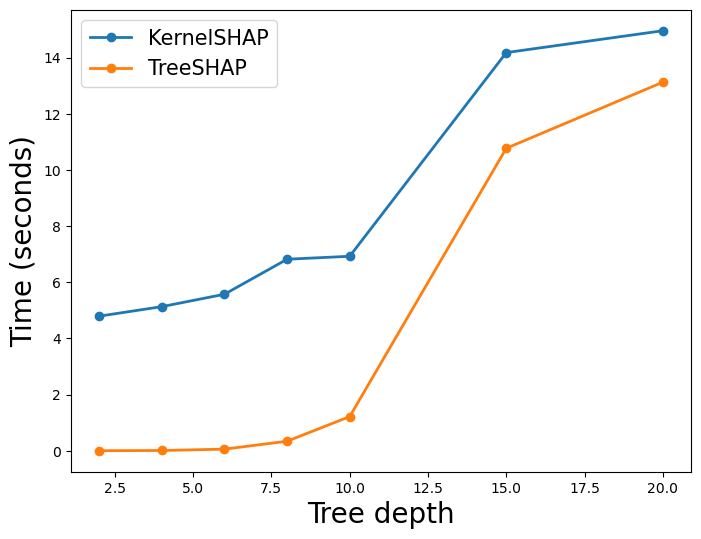
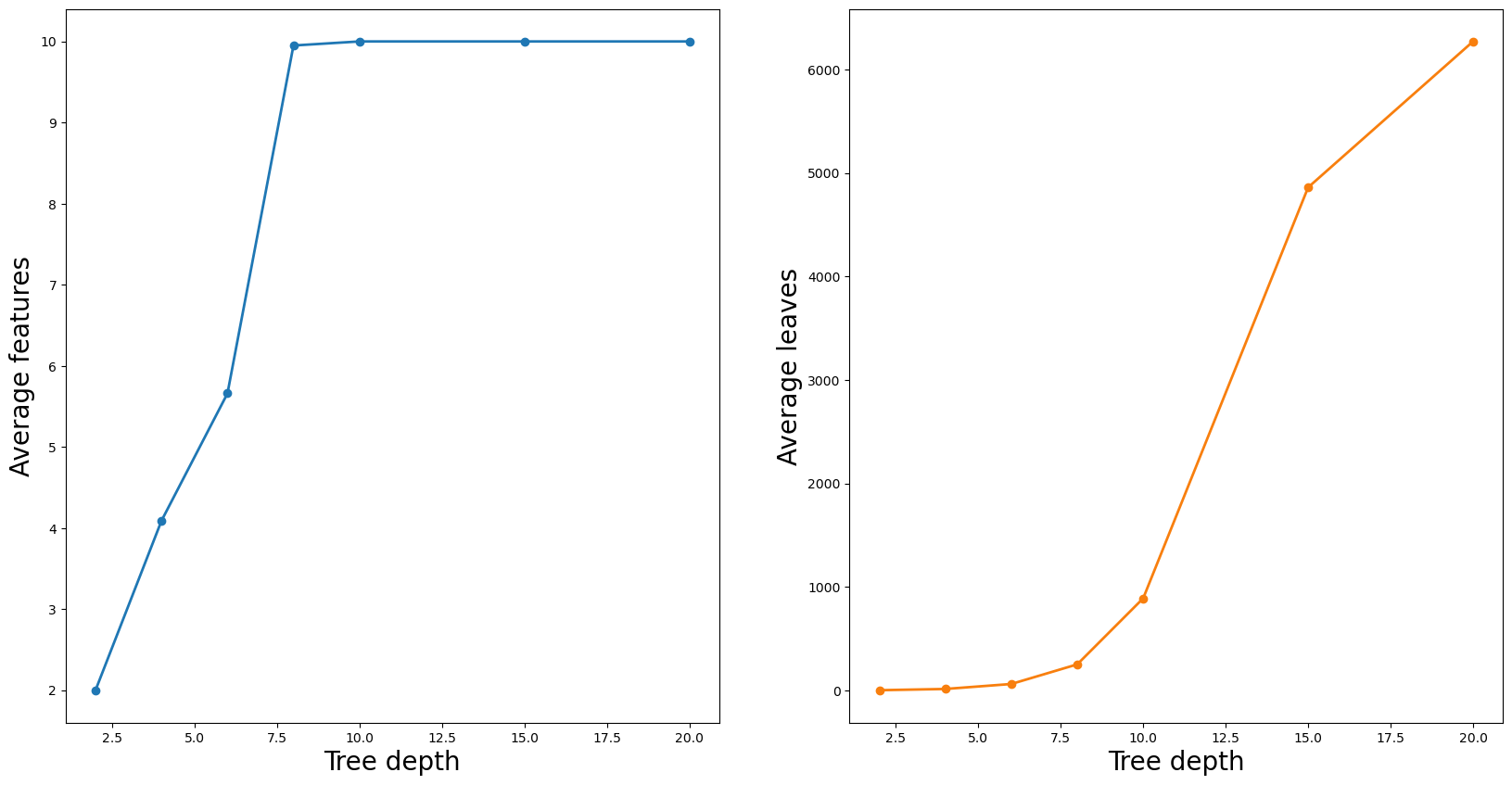
你可能会问为什么 KernelSHAP 时间也会增加。这是因为特征 (M) 和叶子 (L) 的数量会根据树的深度而变化。随着深度的增加，会有更多的分裂，因此我们会有更多的叶子。更多的分裂也意味着树可以使用更多的特征。你可以在 图 6 中看到这一点。这里我们计算了森林中所有树的平均特征和叶子数量。

模型验证和数据探索的要点

通过改变深度，我们发现在某些情况下 TreeSHAP 的计算成本更高。但是，这些情况不太可能发生。我们发现，只有当树的深度为 20 时才会发生这种情况。使用这么深的树并不常见。在实践中，我们通常会拥有比树深度 (D) 更多的特征 (M)。 这意味着，在使用 SHAP 验证树模型时，TreeSHAP 通常是更好的选择。我们能够更快地计算 SHAP 值。这可以同时进行，尤其是当你需要比较多个模型时。对于模型验证，我们对参数 T 、 L 、 D 和 M 没有太多选择。这是因为我们只想验证表现最佳的模型。 对于数据探索，我们拥有更多的灵活性。树算法可用于查找重要的非线性关系和相互作用。为此，我们的模型只需足够好以捕捉数据中的潜在趋势即可。我们可以通过减少树的数量 (T) 和树的深度 (D) 来使用 TreeSHAP 加速此过程。同时，我们能够探索许多模型特征 (M)，而无需大幅提高速度。

其他考虑因素

在选择方法时，时间复杂度是一个重要因素。在做出选择之前，你可能还需要考虑其他一些差异。其中包括 KernelSHAP 与模型无关、方法受特征依赖性的影响，并且只有 TreeSHAP 可用于计算交互效应。

与模型无关

一开始，我们提到 TreeSHAP 最大的限制是它不是模型无关的。如果你正在使用非基于树的算法，你将无法使用它。神经网络也有自己的近似方法。你可以将 DeepSHAP 用于这些算法。然而，KernelSHAP 是唯一可以与所有算法一起使用的方法。

功能依赖项

特征依赖性可能会扭曲 KernelSHAP 的近似值。该算法通过随机采样特征值来估计 SHAP 值。问题是，当特征相关时，采样值可能不太可能。这意味着在使用 SHAP 值时，我们可能会过分重视不太可能的观察结果。 TreeSHAP 没有这个问题。但是，由于特征依赖性，该算法存在不同的问题。即对预测没有影响的特征可以获得非零的 SHAP 值。当该特征与另一个确实影响预测的特征相关时，就会发生这种情况。在这种情况下，我们可以错误地得出某个特征对预测有贡献的结论。

分析互动

SHAP 交互值是 SHAP 值的扩展。它们的工作原理是将特征的贡献分解为其主要影响和交互影响。对于给定的特征，交互影响是它与其他特征的所有联合贡献。在突出显示和可视化数据中的交互时，这些非常有用。我们将在文章《[分析与 SHAP 的相互作用]》中深入探讨这一点。

如果你想使用 SHAP 交互值，则必须使用 TreeSHAP。这是因为它是唯一已实现交互值的近似方法。这与 SHAP 交互值的复杂性有关。KernelSHAP 需要更长的时间来估计这些值。

最后，你应该尽可能使用 TreeSHAP。它速度更快，并能让你分析交互。对于数据探索，你可能希望坚持使用树算法来获得这些好处。如果你正在使用其他类型的算法，那么你必须坚持使用 KernelSHAP。它仍然是一种比蒙特卡罗采样等其他方法更快的近似方法。

参考

S. Lundberg, SHAP Python package (2021), https://github.com/slundberg/shap

S. Lundberg & S. Lee, A Unified Approach to Interpreting Model Predictions (2017), https://arxiv.org/pdf/1705.07874.pdf

S. Lundberg, S.M., G. Erion, G.G. and Lee, S.I., (2018). Consistent individualized feature attribution for tree ensembles. arXiv preprint arXiv:1802.03888.

C. Molnar, Interpretable Machine Learning (2021) https://christophm.github.io/interpretable-ml-book/shap.html

S. Masís, Interpretable Machine Learning with Python (2021)

---

希望这篇文章对你有所帮助！你还可以阅读我的其他文章，或者查看有关企业 AI 实战项目的教程，相信会让你拥有更多收获。

「AI秘籍」系列课程：

• 人工智能应用数学基础
• 人工智能Python基础
• 人工智能基础核心知识
• 人工智能BI核心知识
• 人工智能CV核心知识

---

1. Github, https://github.com/hivandu/public_articles/blob/main/src/interpretable_ml/SHAP/kernelSHAP_vs_treeSHAP.ipynb↩︎