发表AI

分类特征的 SHAP

将经过One-Hot 编码转换的分类特征的 SHAP 值相加

可直接在橱窗里购买，或者到文末领取优惠后购买：

img

分类特征需要先进行转换，然后才能用于模型。One-Hot 编码是一种常见的方法：我们最终会得到每个类别的二进制变量。这很好，直到理解使用 SHAP 的模型为止。每个二进制变量都有自己的 SHAP 值。这使得很难理解原始分类特征的整体贡献。

一种简单的方法是将每个二进制变量的 SHAP 值加在一起。这可以解释为原始分类特征的 SHAP 值。我们将向你介绍执行此操作的 Python 代码。我们将看到我们能够使用 SHAP 聚合图。但是，在理解分类特征关系的性质时，这些是有限的。所以，最后我们向你展示如何使用箱线图来可视化 SHAP 值。

如果你不熟悉 SHAP 或 Python 包，我建议你阅读一下之前的这篇文章《[[Python 中的 SHAP 简介]]》。我们将深入探讨如何解释 SHAP 值。我们还探讨了本文中使用的一些聚合。

处理分类变量时还有另一种解决方案。那就是使用 CatBoost 进行建模。关于 CatBoost 如何进行建模，我以后会写一篇相关文章《[使用 CatBoost 实现分类特征的 SHAP]》，你可以在其中找到此解决方案。

数据集

为了演示分类特征的问题，我们将使用蘑菇分类数据集。你可以在图 1 中看到此数据集的快照。目标变量是蘑菇的类别。也就是说，蘑菇是有毒 (p) 还是可食用 (e)。你可以在UCI 的 MLR1中找到此数据集。

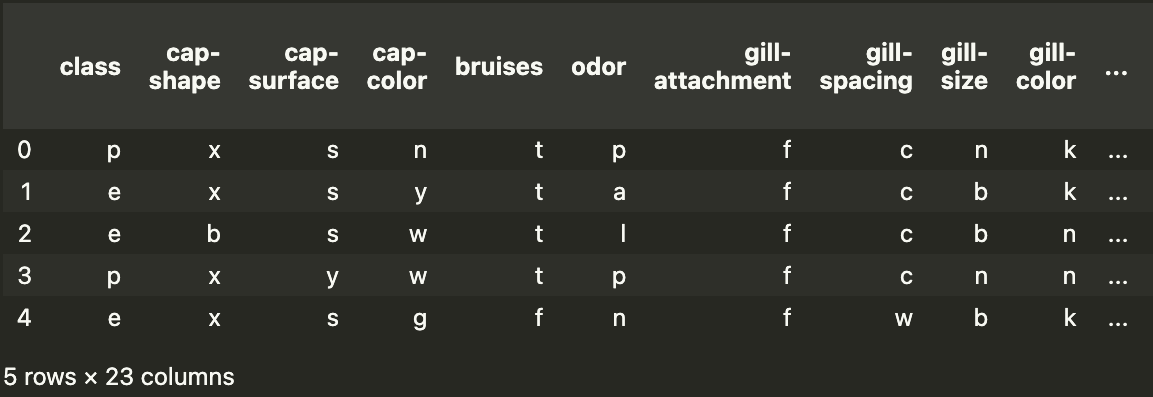
图 1：蘑菇数据集快照

对于模型特征，我们有 22 个分类特征。对于每个特征，类别都用一个字母表示。例如，气味有 9 个独特的类别 - almond (a)、anise (l)、creosote (c), fishy (y), foul (f), musty (m), none (n), pungent (p), spicy (s)。这就是蘑菇的气味。

建模

我们将向你介绍用于分析此数据集的代码，你可以在GitHub2上找到完整的脚本。首先，我们将使用下面的 Python 包。我们有一些用于处理和可视化数据的常用包（第 1-5 行）。我们使用 OneHotEncoder 来转换分类特征（第 7 行）。我们使用 xgboost 进行建模（第 10 行）。最后，我们使用 shap 来了解我们的模型是如何工作的（第 12 行）。

1
2
3
4
5
6
7
8
9
10
11
12
13
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use('default')

from sklearn.preprocessing import OneHotEncoder
from sklearn.metrics import accuracy_score,confusion_matrix

import xgboost as xgb

import shap
shap.initjs()

我们导入数据集（第 2 行）。我们需要一个数值目标变量，因此我们通过设置 toxicous = 1 和 edible = 0 来转换它（第 6 行）。我们还获得了分类特征（第 7 行）。我们不使用 X_cat 进行建模，但它以后会派上用场。

1
2
3
4
5
6
7
# load data 
data = pd.read_csv(dp + "mushrooms.csv")

# get features
y = data['class']
y = y.astype('category').cat.codes
X_cat = data.drop('class', axis=1)

要使用分类特征，我们还需要对其进行转换。我们首先安装一个编码器（第 2-3 行）。然后我们使用它来转换分类特征（第 6 行）。对于每个分类特征，每个类别都有一个二进制特征。我们为每个二进制特征创建特征名称（第 9 至 10 行）。最后，我们将它们放在一起以创建特征矩阵（第 12 行）。

1
2
3
4
5
6
7
8
9
10
11
12
# fit encoder
enc = OneHotEncoder()
enc.fit(X_cat)

# transform categorical features
X_encoded = enc.transform(X_cat).toarray()

# create feature matrix
feature_names = X_cat.columns
new_feature_names = enc.get_feature_names_out(feature_names)

X = pd.DataFrame(X_encoded, columns= new_feature_names)

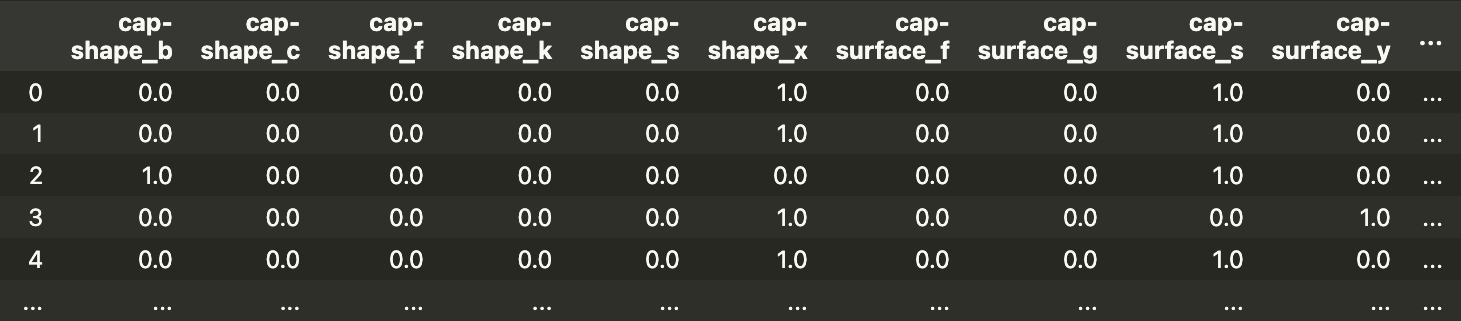
最终，我们得到了 117 个特征。你可以在图 2 中看到特征矩阵的快照。例如，你可以看到 cap-shape 现已转换为 6 个二进制变量。特征名称末尾的字母来自原始特征的类别。

图2：X特征矩阵

我们使用此特征矩阵训练模型（第 2-5 行）。我们使用 XGBClassifier。XGBoost 模型由 10 棵树组成，每棵树的最大深度为 2。该模型在训练集上的准确率为 97.7%。

1
2
3
4
5
# Train model
model = xgb.XGBClassifier(objective="binary:logistic", 
                         max_depth=2, 
                         n_estimators=10)
model.fit(X, y)

标准 SHAP 值

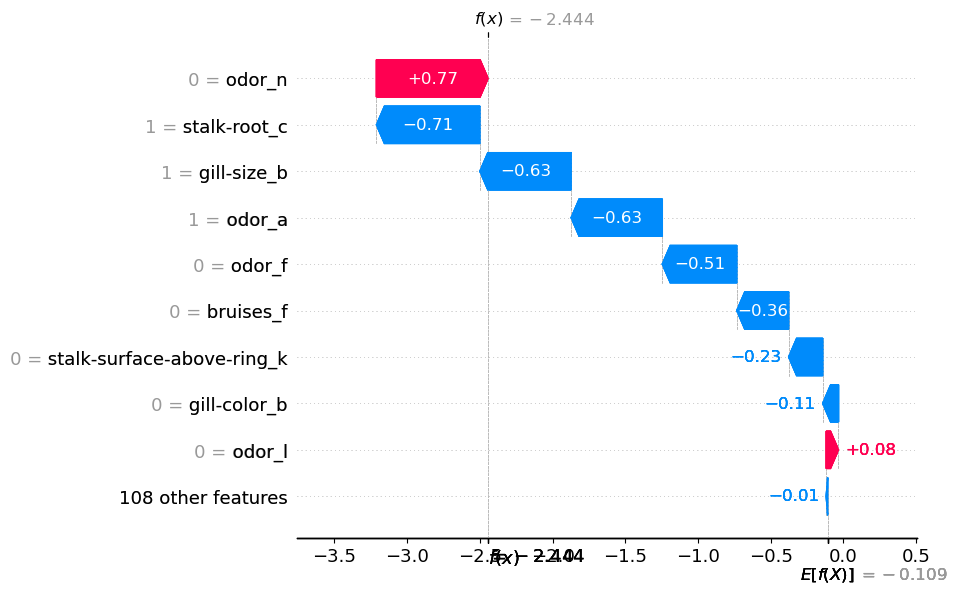
此时，我们想了解模型是如何做出这些预测的。我们首先计算 SHAP 值（第 2-3 行）。然后，我们使用瀑布图（第 6 行）可视化第一个预测的 SHAP 值。你可以在图 3 中看到此图。

1
2
3
4
5
6
# get shap values
explainer = shap.Explainer(model)
shap_values = explainer(X)

# waterfall plot
shap.plots.waterfall(shap_values[1], show=False)

你可以看到每个二元特征都有自己的 SHAP 值。以气味为例。它在瀑布图中出现了 4 次。odor_n = 0 增加了蘑菇有毒的概率。同时，odor_a = 1、odor_f = 0 和 odor_I = 0 都降低了概率。蘑菇气味的总体贡献是什么尚不清楚。在下一节中，我们将看到，当我们将所有单独的贡献加在一起时，它确实变得清晰起来。

图 3：第一次观察的瀑布图

分类特征的 SHAP

让我们从探索shap_values对象开始。我们在下面的代码中打印该对象。你可以在下面的输出中看到它由 3 个组件组成。我们有每个预测的SHAP 值 ( values )。数据给出了二进制特征的值。每个预测也将具有相同的基值 ( base_values )。这是平均预测对数概率。

1
print(shap_values)

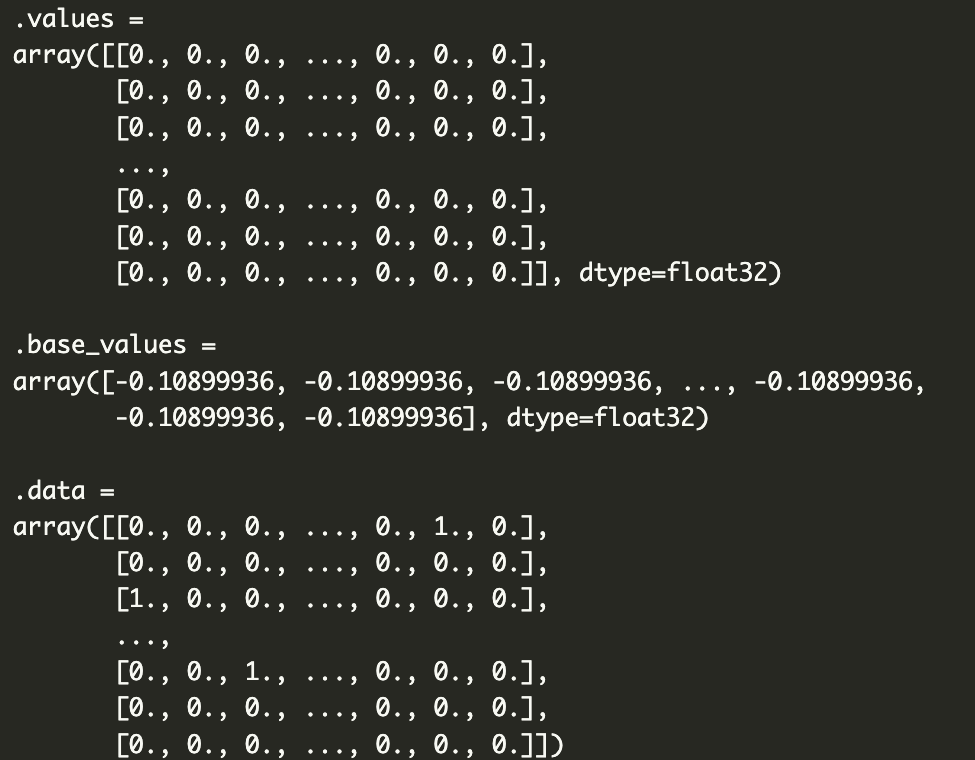
image-20240728190810728

我们可以通过在下面打印它们来仔细查看第一个预测的 SHAP 值。一共有 117 个值。每个二进制变量一个。SHAP 值的顺序与 X 特征矩阵相同。请记住，第一个分类特征cap-shape有 6 个类别。这意味着前 6 个 SHAP 值对应于此特征的二进制特征。接下来的 4 个对应于cap-surface特征，依此类推。

1
print(shap_values.values[1])

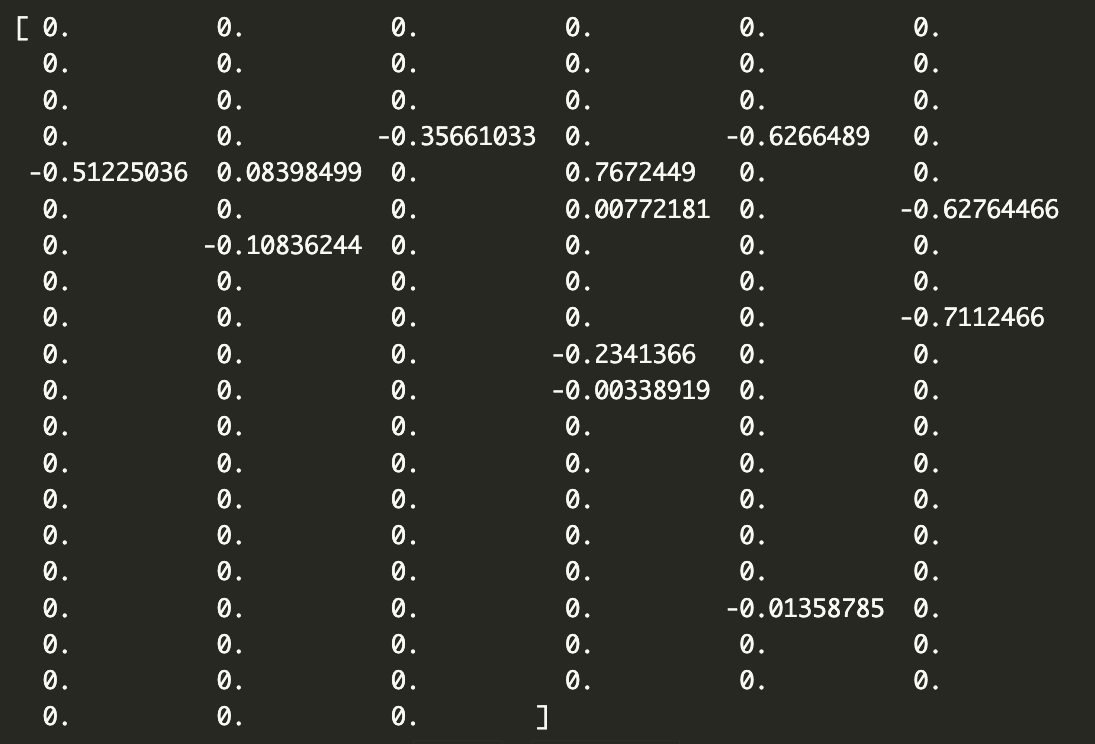
image-20240728190927132

我们希望将每个分类特征的 SHAP 值加在一起。为此，我们首先创建n_categories数组。它包含每个分类变量的唯一类别数。数组中的第一个数字将是 6（表示帽形），然后是 4（表示帽表面），依此类推……

1
2
3
4
5
# get number of unique categories for each feature 
n_categories = []
for feat in feature_names[:-1]:
    n = X_cat[feat].nunique()
    n_categories.append(n)

我们使用n_categories来拆分 SHAP 值数组（第 5 行）。我们最终得到一个子列表。然后我们对每个子列表中的值求和（第 8 行）。通过这样做，我们将 SHAP 值从 117 个减少到 22 个。我们对shap_values对象中的每个观察值都执行此操作（第 2 行）。对于每次迭代，我们将求和的 shap 值添加到new_shap_values数组（第 10 行）。

1
2
3
4
5
6
7
8
9
10
new_shap_values = []
for values in shap_values.values:
    
    # split shap values into a list for each feature
    values_split = np.split(values , np.cumsum(n_categories))
    
    # sum values within each list
    values_sum = [sum(l) for l in values_split]
    
    new_shap_values.append(values_sum)

现在，我们需要做的就是用新值替换原始 SHAP 值（第 2 行）。我们还用原始分类特征中的类别字母替换二进制特征数据（第 5-6 行）。最后，我们用原始特征名称替换二进制特征名称（第 9 行）。重要的是将这些新值分别作为数组和列表传递。这些是 shap_values 对象使用的数据类型。

1
2
3
4
5
6
7
8
9
# replace shap values
shap_values.values = np.array(new_shap_values)

# replace data with categorical feature values 
new_data = np.array(X_cat)
shap_values.data = np.array(new_data)

# update feature names
shap_values.feature_names = list(X_cat.columns)

更新后的 shap_values 对象可以像原始对象一样使用。在下面的代码中，我们绘制了第一次观察的瀑布图。你会注意到此代码与之前完全相同。

1
2
# waterfall plot
shap.plots.waterfall(shap_values[0])

你可以在图 4 中看到输出。我们现在有 22 个 SHAP 值。你还可以看到左侧的特征值已被类别标签替换。我们之前讨论过气味特征。现在你可以清楚地看到此功能的整体贡献。它使对数概率降低了 0.29。

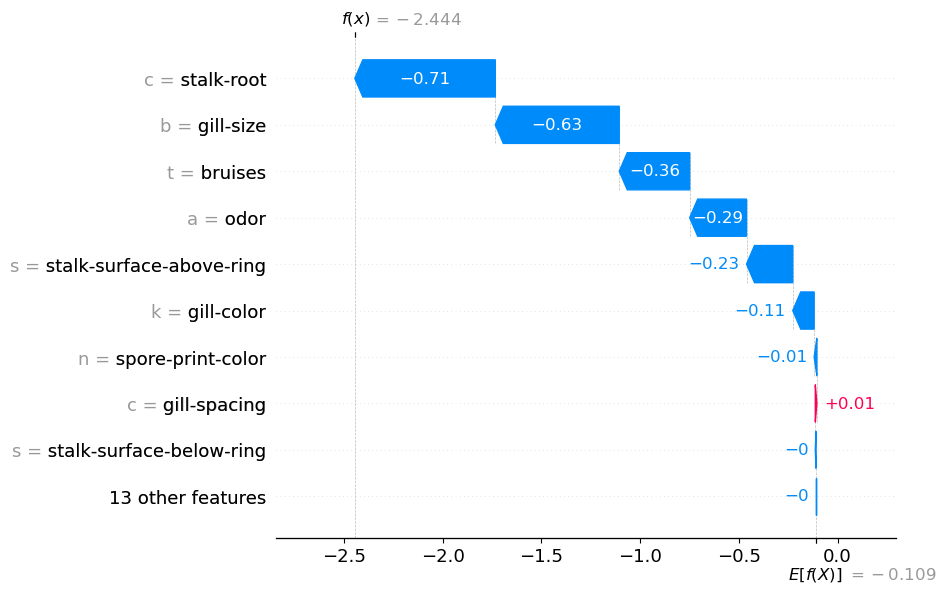
图 4：第一次观察的瀑布图，带有更新的 SHAP 值

在上图中，我们得到气味 = a。这告诉我们蘑菇有“杏仁”气味。我们应避免将该图解释为“杏仁气味降低了对数几率”。我们将多个 SHAP 值相加。因此，我们应该将其解释为“杏仁气味和缺乏其他气味降低了对数几率”。例如，查看第一个瀑布图，缺乏“恶臭”气味（odor_f = 0）也降低了对数几率。

在我们继续聚合这些新的 SHAP 值之前，值得讨论一些理论。我们能够使用 SHAP 值做到这一点的原因是由于它们的可加性。也就是说，平均预测（E[f(x)]）加上所有 SHAP 值等于实际预测（f(x)）。通过将一些 SHAP 值加在一起，我们不会干扰此属性。这就是为什么 f(x) = -2.444 在图 3 和图 4 中相同的原因。

平均 SHAP

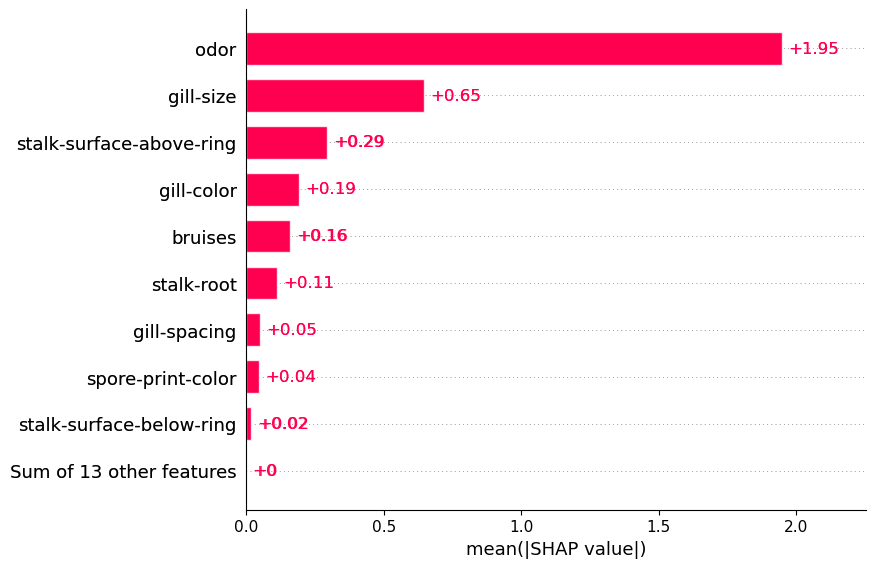
与瀑布图一样，我们可以像使用原始 SHAP 值一样使用 SHAP 聚合。例如，我们在下面的代码中使用平均 SHAP 图。查看图 5，我们可以使用此图突出显示重要的分类特征。例如，我们可以看到气味往往具有较大的正/负 SHAP 值。

1
2
# Mean SHAP
shap.plots.bar(shap_values)

图 5：平均 SHAP

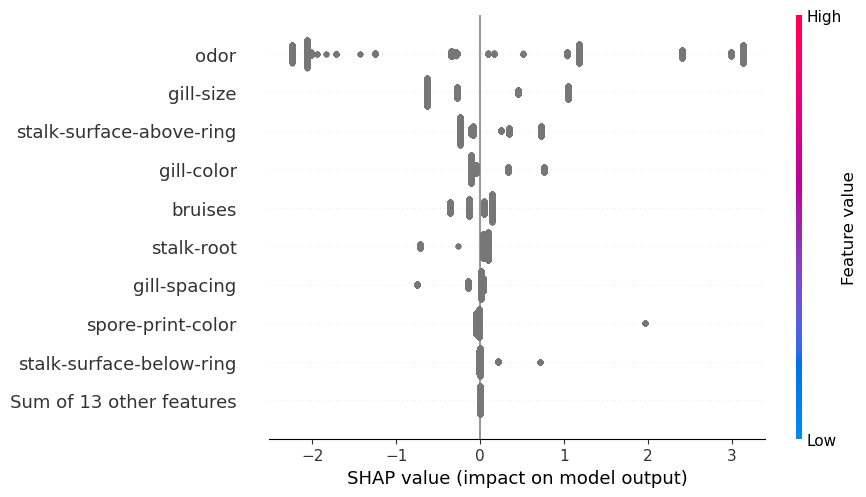
蜂群

另一种常见的聚合是蜂群图。对于连续变量，此图很有用，因为它可以帮助解释关系的性质。我们可以看到 SHAP 值如何与特征值相关联。但是，对于分类特征，我们用标签替换了特征值。因此，在图 6 中，你可以看到 SHAP 值都被赋予了相同的颜色。我们需要创建自己的图来了解这些关系的性质。

1
shap.plots.beeswarm(shap_values)

图 6：分类变量蜂群

SHAP 箱线图

我们可以采用一种方式来做到这一点，即使用 SHAP 值的箱线图。在图 7 中，你可以看到一个气味特征的箱线图。在这里，我们根据气味类别对气味特征的 SHAP 值进行了分组。你可以看到，难闻的气味会导致更高的 SHAP 值。这些蘑菇更有可能有毒。请不要吃任何有异味的蘑菇！同样，没有气味的蘑菇更有可能可以食用。一条橙色线表示这些蘑菇的所有 SHAP 值都相同。

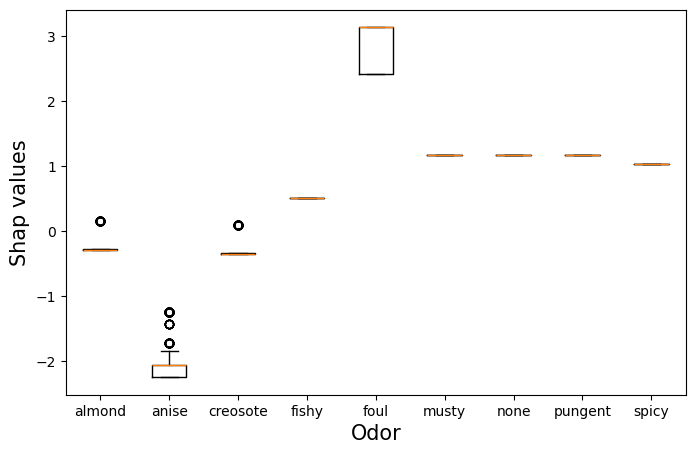
图 7：气味 SHAP 值的箱线图

我们使用以下代码创建此箱线图。我们首先获取气味 SHAP 值（第 2 行）。请记住，这些是更新值。对于每个预测，气味特征只有一个 SHAP 值。我们还获取气味类别标签（第 3 行）。我们根据这些标签分割 SHAP 值（第 6-12 行）。我们使用这些值为每个气味类别绘制一个箱线图（第 28-33 行）。为了使图表更易于解释，我们还用完整的类别名称替换了字母（第 15-25 行）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# get shaply values and data
odor_values = shap_values[:,"odor"].values
odor_data = shap_values[:,"odor"].data

# split odor shap values based on odor category
unique_odor = ['a','l','c','y','f','m','n','p','s']
odor_categories = list(set(odor_data))

odor_groups = []
for o in odor_categories:
    relevant_values = odor_values[odor_data == o]
    odor_groups.append(relevant_values)

# replace categories with labels
odor_labels = {'a':'almond', 
               'c':'creosote', 
               'f':'foul', 
               'l':'anise',
               'm':'musty', 
               'n':'none', 
               'p':'pungent',
               's':'spicy',
               'y':'fishy',}

labels = [odor_labels[u] for u in unique_odor]

# plot boxplot
plt.figure(figsize=(8, 5))

plt.boxplot(odor_groups,labels=labels)

plt.ylabel('Shap values',size=15)
plt.xlabel('Odor',size=15)

实际上，你的特征中可能只有少数是分类的。你需要更新上述过程以仅对分类特征求和。你还可以想出自己的方法来可视化这些特征之间的关系。如果你想出了另一种方法，我很乐意在评论中听到它。

我还想了解特征依赖关系将如何影响此分析。根据定义，转换后的二进制特征将是相关的。这会影响 SHAP 值的计算。我们正在使用 TreeSHAP 来估计 SHAP 值。我的理解是，这些值不像 KernelSHAP 那样受依赖关系的影响。我很想在评论中听听你的想法。

参考

S. Lundberg，SHAP Python 包(2021) ， https://github.com/slundberg/shap

S. Lundberg 和 S. Lee，《解释模型预测的统一方法》 (2017)，https://arxiv.org/pdf/1705.07874.pdf

希望这篇文章对你有所帮助！你还可以阅读我的其他文章，或者查看有关企业 AI 实战项目的教程，相信会让你拥有更多收获。

「AI秘籍」系列课程：

AI企业项目实战课优惠二维码

  1. Dataset, https://archive.ics.uci.edu/ml/datasets/Mushroom↩︎

  2. Github, https://github.com/hivandu/medium-articles/blob/master/src/interpretable_ml/SHAP/SHAP_categorical.ipynb↩︎

分类特征的 SHAP

https://hivan.me/分类特征的 SHAP/

作者

Hivan Du

发布于

2024-09-06

更新于

2024-09-20

许可协议

#

喜欢这篇文章？打赏一下作者吧

评论

关注我

链接

分类

最新文章

×