25. 深度学习进阶 - 权重初始化，梯度消失和梯度爆炸

Hi，你好。我是茶桁。

咱们这节课会讲到权重初始化、梯度消失和梯度爆炸。咱们先来看看权重初始化的内容。

权重初始化

机器学习在我们使用的过程中的初始值非常的重要。就比如最简单的wx+b，现在要拟合成一个 yhat，w 如果初始的过大或者初始的过小其实都会比较有影响。

假设举个极端情况，就是 w 拟合的时候刚刚就拟合到了离 x 很近的地方，我们想象一下，这个时候是不是学习起来就会很快？所以对于深度学习模型权重的初始化是一个非常重要的事情，甚至有人就说把初始化做好了，其实绝大部分事情就已经解决了。

那么我们怎么样获得一个比较好的初始化的值？首先有这么几个原则

• 我们的权重值不能设置为 0。
• 尽量将权重变成一个随机化的正态分布。而且有更大的 X 输入，那我们的权重就应该更小。

\[ \begin{align*} loss & = \sum(\hat y - y_i)^2 \\ & = \sum(\sum w_ix_i - y_i)^2 \end{align*} \]

我们看上面的式子，yhat 就是 w_i*x_i, 这个时候 x_i 可能是几百万，也可能是几百。我们 w_i 取值在(-n, n)之间，那当 x_i 维度特别大的时候，那 yhat 值算出来的也就会特别大。所以，x_i 的维度特别大的时候，我们期望 w_i 值稍微小一些，否则加出来的 yhat 可能就会特别大，那最后求出来的 loss 也会特别大。

如果 loss 值特别大，可能就会得到一个非常的梯度。那我们知道，学习的梯度特别大的话，就会发生比较大的震荡。

所以有一个原则，就是当 x 的 dimension 很大的时候, 我们期望的它的权重越小。

那后来就有人提出来了一个比较重要的初始化方法，Xavier 初始化。这个方法特别适用于 sigmoid 激活函数或反正切 tanh 激活函数，它会根据前一层和当前层的神经元数量来选择初始化的范围，以确保权重不会过大或过小。 \[ \begin{align*} 均值为 0 和标准差的正态分布: \sigma & = \sqrt{\frac{2}{n_{inputs}+n_{outputs}}} \\ -r 和+r 之间的均匀分布：r & = \sqrt{\frac{6}{n_{inputs}+n_{outputs}}} \end{align*} \]

然后 W 的均匀分布就会是这样： \[ W \sim U \Bigg \vert -\frac{\sqrt 6}{\sqrt{n_j + n_{j+1}}}, \frac{\sqrt 6}{\sqrt{n_j + n_{j+1}}} \]

这个是一个比较有名的初始化方法，如果要做函数的初始化的话，PyTorch 在 init 里面有一个方法：

torch.nn.init.xavier_uniform_(tensor, gain=1.0)

比如，我们看这样例子：

w = torch.empty(3, 5)
nn.init.xavier_uniform_(w, gain=nn.calculate_gain('relu'))

注意: init 方法里还有其他的一些方法，大家可以查阅 PyTorch 的相关文档：https://pytorch.org/docs/stable/nn.init.html

梯度消失与梯度爆炸

当我们的模型层数特别多的时候

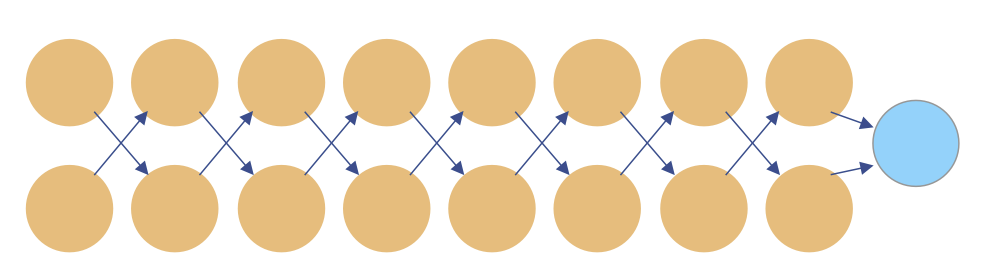
就比如我们上节课用到的 Sequential，我们可以在里面写如非常多的一个函数：

model = nn.Sequential(
    nn.Linear(in_features=10, out_features=5).double(),
    nn.Sigmoid(),
    nn.Linear(in_features=5, out_features=8).double(),
    nn.Sigmoid(),
    nn.Linear(in_features=8, out_features=8).double(),
    nn.Sigmoid(),
    ...
    nn.Linear(in_features=8, out_features=8).double(),
    nn.Softmax(),
)

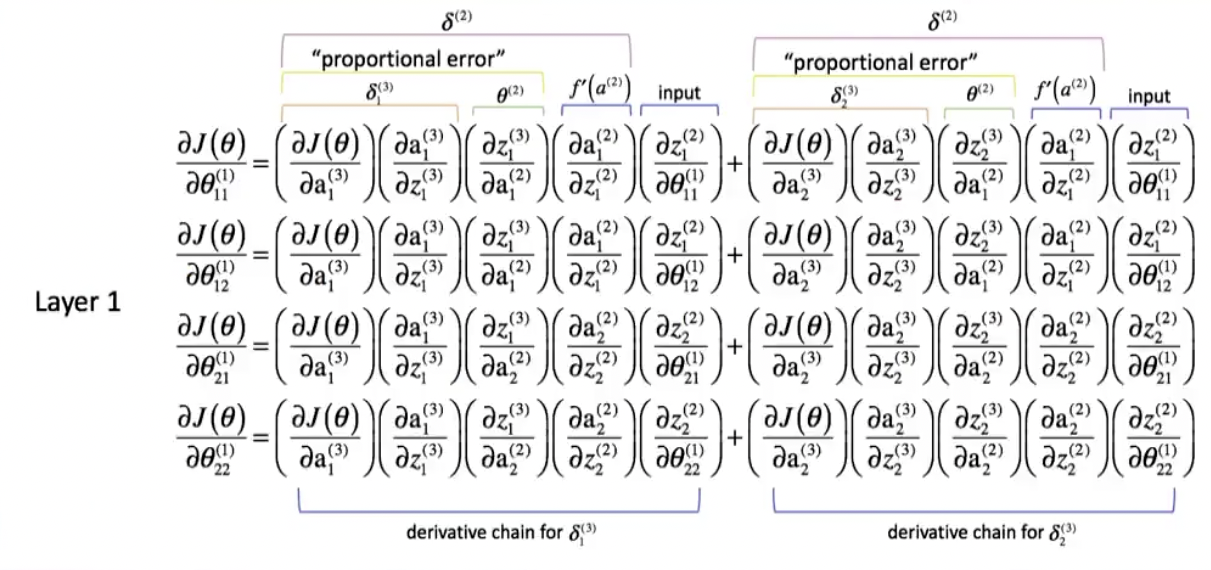
这样，在做偏导的时候我们其中几个值特别小，那两个一乘就会乘出来一个特别特别小的数字。最后可能会导致一个结果，\(\frac{\partial loss}{\partial wi}\)的值就会极小，它的更新就会特别的慢。我们把这种东西就叫做梯度消失，也有人叫梯度弥散。

以 Sigmoid 函数为例，其导数为

\[ \begin{align*} \sigma '(x) = \sigma(x)(1-\sigma(x)) \end{align*} \]

在 x 趋近正无穷或者负无穷时，导数接近 0。当这种小梯度在多层网络中相乘的时候，梯度会迅速减小，导致梯度消失。

除此之外还有一种情况叫梯度爆炸，剃度爆炸类似，当模型的层很多的时候，如果其中某两个值很大，例如两个 10^2，当这两个乘起来就会变成 10^4。乘下来整个 loss 很大，又会产生一个结果，我们来看这样一个场景：

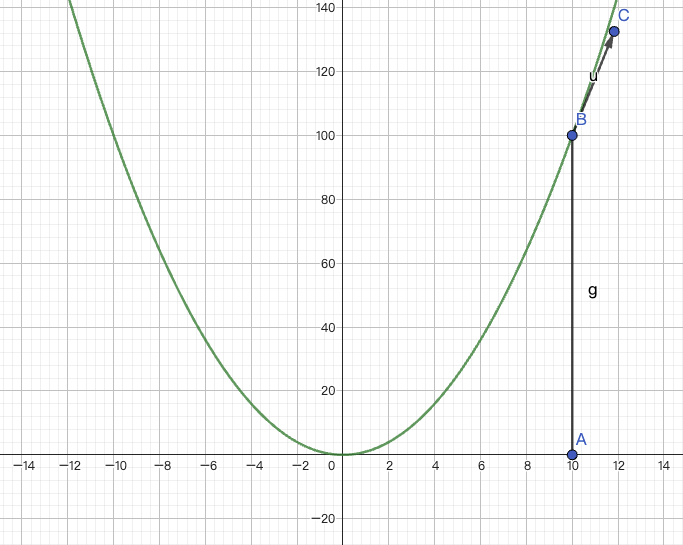
假如说对于上图中这个函数来说，横轴为 x, 竖轴为 loss，对于这个 xi 来说，这个地方\(\frac{\partial loss}{\partial xi}\)已经是一个特别大的数字了。

假设咱们举个极端的情况（忽略图中竖轴上的数字），我们现在 loss 等于 x^4：\(loss=x^4\)，然后现在\(\frac{\partial loss}{\partial x^4}\)就等于\(4x^3\)，我们假设 x 在 A 点，当 x=10 的时候，那\(4\times x^3 = 4000\)， 那我们计算新的 xi，就是\(x_i = x_i - \alpha \cdot \frac{\partial loss}{\partial x_i}\)，现在给 alpha 一个比较小的数，我们假设是 0.1，那式子就变成\(10 - 0.1 \times 4000\)，结果就是-390。

我们把它变到-390 之后，本来我们本来做梯度下降更新完，xi 期望的是 loss 要下降，但是我们结合图像来看，xi=-390 的时候，loss 就变得极其的巨大了，然后我们在继续，(-390)^4， 这个 loss 就已经爆炸了。

再继续的时候，会发现会在极值上跳来跳去，loss 就无法进行收敛了。所以我们也要拒绝这种情况的发生。

那梯度消失和梯度爆炸这两个问题该如何解决呢？我们来看第一种解决方法： Batch normalization，批量归一化。

那这个方法的核心思想是对神经网络的每一层的输入进行归一化，使其具有零均值和单位方差。

那么首先，对于每个 mini-batch 中的输入数据，计算均值和方差。\(B = \{x_1...m\}\); 要学习的参数: \(\gamma,\beta\)。

\[ \begin{align*} \mu_B & = \frac{1}{m}\sum^m_{i=1}x_i \\ \sigma ^2_B & = \frac{1}{m}\sum_{i=1}^m(x_i-\mu_B)^2 \\ & \mu 为均值 mean， \sigma 为方差 \end{align*} \]

这里和咱们之前讲 x 做 normalization 的时候其实是特别相似，基本上就是一件事。

然后我们使用均值和方差对输入进行归一化，使得其零均值和单位方差，即将输入标准化为 xhat。

\[ \begin{align*} \hat x_i = \frac{x_i - \mu_B}{\sqrt{\sigma ^2_B + \varepsilon}} \end{align*} \]

接着我们对归一化后的输入应用缩放和平移操作，以允许网络学习最佳的变换。

\[ \begin{align*} y_i = \gamma \hat x_i + \beta \equiv BN_{\gamma,\beta}(x_i) \end{align*} \]

输出为\(\{y_i = BN_{\gamma,\beta}(x_i)\}\)。

最后将缩放和平移后的数据传递给激活函数进行非线性变换。

它会输入一个小批量的 x 值，

经过反复的梯度下降，会得到一个 gamma 和 beta，能够知道在这一步 x 要怎么样进行缩放，在缩放之前会经历刚开始的时候那个 normalization 一样，把把过小值会变大，把过大值会变小。

我们在之前的课程中演示过，没看过和忘掉的同学可以往前翻看一下。

然后在经过这两个可学习的参数进行一个变化，这样它可以做到在每一层 x 变化不会极度的增大或者极度的缩小，可以让我们的权值保持的比较稳定。

那除了 Batch normalization 之外，还有一个方法叫 Gradient clipping， 它是可以直接将过大的梯度值变小。

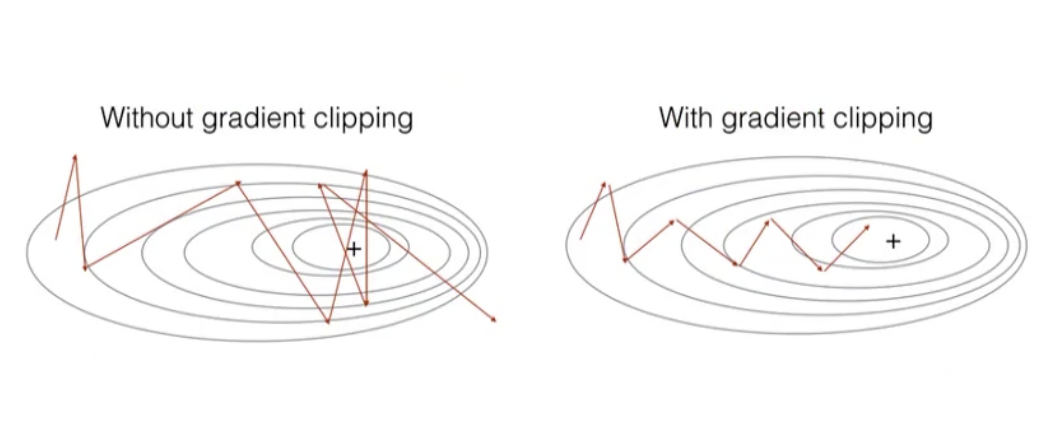
它其实很简单，也叫做梯度减脂。

如果我们求解出来\(\frac{\partial loss}{\partial w_i}\)很大，假设原来等于 400，我们定义了一个 100，那超过 100 的部分，就全部设置成 100。

train_loss.backward()
pt.nn.units.clip_grad_value_(model.parameters(), 100)
optimizer.step()

简单粗暴。那其实梯度爆炸还是比较容易解决的，比较复杂的其实是梯度消失的问题。

梯度爆炸为什么比较容易解决？梯度爆炸起码是有导数的，只要把这个导数给它放的特别小就行了，有导数起码保证 wi 可以更新。

假设 alpha，我们的 learning_rate 等于 0.01，乘上一个 100，可以保证每次可以有个变化。但是每次这个梯度特别小，假如都快接近于 0 了，那么 1e-10, 就算乘上 100 倍，最后还是一个特别小的数字。所以相较而言，梯度爆炸就更好解决一些，方法更粗暴一些。

补充一个知识点，这个虽然现在已经用不到了，但是对我们的理解还是有帮助的。方法比较古老。

就是当我们发现梯度有问题的时候， 大概在 10 年前，那个时候神经网络的模块也不太丰富，很多新出的 model，做神经网络的人，一些导数，传播什么的都需要自己写，就我们前几节课写那个神经网络框架的时候做的事。

有的时候导数写错了，就有一种方法叫做 gradient checking，梯度检查。

这个使用场景非常的少，当你自己发明了一个新的模块，加到这个模型里面的时候会遇到。

其实很简单，就是把最终的\(\frac{\partial loss}{\partial w_i}\)，求解出来的偏导总是不收敛，可能是这个偏导有问题，那么有可能求导的函数写错了。

那在这个时候就可以做个简单的变化：

\[ \begin{align*} \frac{\partial loss(\theta+\varepsilon)-\partial loss(\theta - \varepsilon)}{2\varepsilon} \end{align*} \]

这其中\(\partial loss(\theta + \varepsilon)\)和\(\partial loss(\theta - \varepsilon)\)是在参数\(\theta\), 其实也就是我们的 wi 上添加和减去微小扰动 theta 后的损失函数值。

然后我们计算数值梯度和反向传播计算得到的梯度之间的差异。通常这是通过计算它们之间的差异来完成，然后将其与一个小的阈值，比如 1e-7 进行比较。如果差异非常小（小于阈值），则可以认为梯度计算是正确的，否则可能就需要从新写一下偏导函数了。

这个比较难，但不是一个重点，当且仅当自己要发明一个模型的时候。

那接下来我们来看一下关于 Learning_rate 和 Early Stopping 的问题。

理论上，如果深度学习效果不好，那么我们可以将 learning rate 调小，可以让所有模型效果变得更好，它可以让所有的 loss 下降。

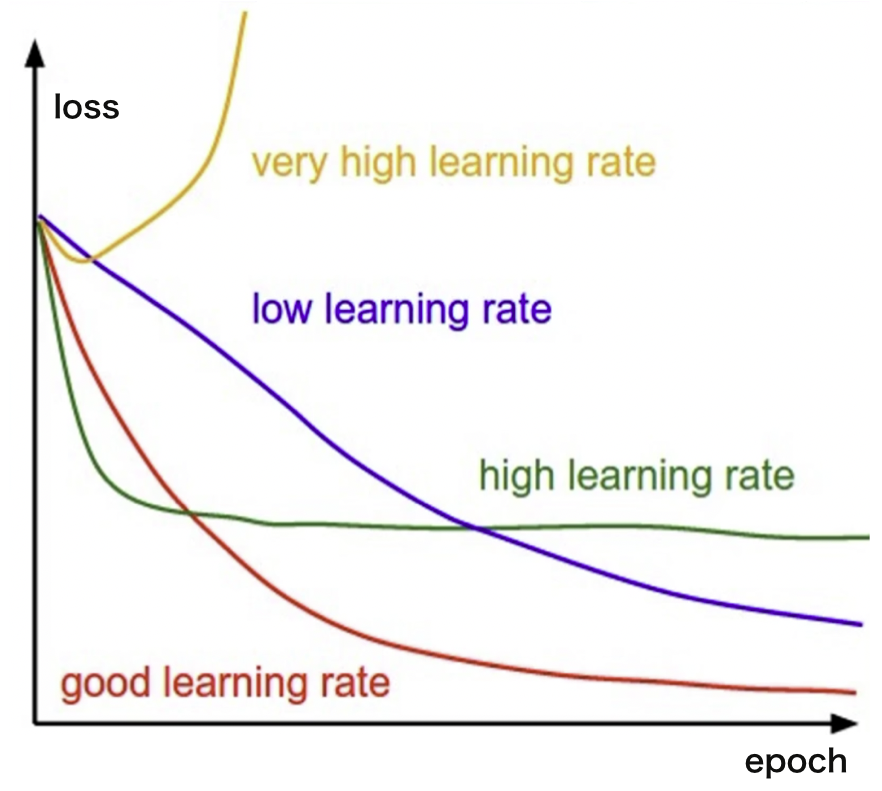
但是如果你的 learning rate 变得特别小，假如说是 1e-9，那这样的结果就是 w 的变化会非常的慢，训练时间就变得很长。为了解决这个问题，就有一些比较简单的方法。

第一个，我们可以把 learning rate 和 loss 设置成一个相关的函数，例如说 loss 越小的时候，Learning rate 越小，或者随着 epoch 的增大，loss 越小。这个就叫 learning rate 的 decay。

将 learning rate 或者训练次数和 loss 设置成一个相关的函数，那么越到后面效果越好的时候，learning rate 就会越小。

还有，我们可能会发现 loss 连续 k 次不下降，那我们就可以提前结束训练过程，这个就是 Early Stopping。

也就是当你发现 loss 连续 k 次不下降，或者甚至于在上升，那么这个时候，就可以将最优的这个值给它记录下来。

咱们可能会经常出现的情况就是值在那里震荡，本来呢已经快接近于最优点了，可是震荡了几次之后，还可能震荡出去了，loss 变大了。或者就一直在这个震荡里边出不去，这个时候多学习也没有用，所以就可以早点停止，这个就是 Early Stopping，中文有人称呼它为早停方法。

好，下节课，咱们要讲一个重点，也是一个难点。就是咱们做机器学习的时候，不同的优化方法。