分析机器学习的公平性

进行探索性公平性分析，并使用平等机会、均等几率和不同影响来衡量公平性

「AI秘籍」系列课程：

• 人工智能应用数学基础

• 人工智能Python基础

• 人工智能基础核心知识

• 人工智能BI核心知识

• 人工智能CV核心知识

仅仅建立能够做出准确预测的模型已经不够了。我们还需要确保这些预测是公平的。

这样做可以减少有偏见的预测带来的危害。因此，你将在建立对人工智能系统的信任方面大有裨益。要纠正偏见，我们需要从分析数据和模型的公平性开始。

衡量公平性很简单。

理解某个模型不公平的原因则更加复杂。

这就是为什么我们将：

• 首先进行探索性公平性分析——在开始建模之前识别潜在的偏见来源。
• 然后，我们将继续衡量公平性——通过应用公平的不同定义。

你可以在下面看到我们将介绍的方法的摘要。

我们将讨论这些方法背后的理论。我们还将使用 Python 应用它们。我们将讨论关键代码，你可以在GitHub¹上找到完整的项目。

数据集

我们将使用成人数据集构建一个模型²。你可以在表 1中看到它的快照。经过一些特征工程后，我们将使用前 6 列作为模型特征。接下来的 2 列（种族和性别）是敏感属性。我们将根据这些分析对群体的偏见。最后一个是我们的目标变量。我们将尝试预测一个人的收入是高于还是低于 5 万美元。

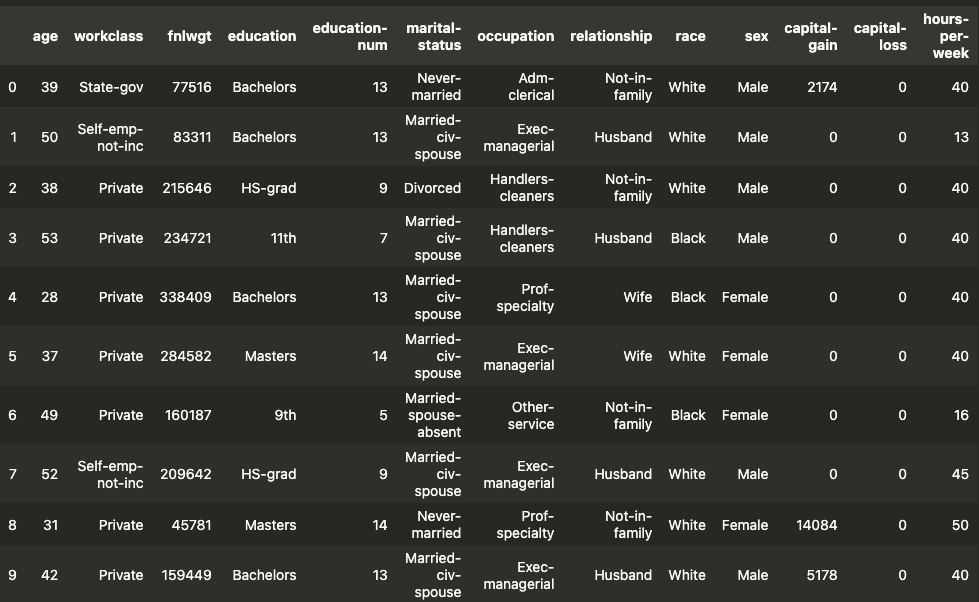
在加载此数据集之前，我们需要导入一些 Python 包。我们使用下面的代码执行此操作。我们使用NumPy和 Pandas 进行数据处理（第 1-2 行）。Matplotlib用于一些数据可视化（第 3 行）。我们将使用 xgboost 来构建我们的模型（第 5 行）。我们还从 scikit-learn 导入了一些函数来评估我们的模型（第 8-10 行）。确保你已安装这些。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

import xgboost as xgb
from xgboost import plot_importance

from sklearn.metrics import accuracy_score,confusion_matrix
from sklearn.metrics import classification_report
from sklearn.feature_selection import mutual_info_classif

import shap
import os

data_path = os.environ.get('pub_data')

我们在下面导入数据集（第 7 行）。还删除了任何有缺失值的行（第 8 行）。请注意，这里加载了一些额外的列。请参阅列名（第 1-4 行）。在本分析中，我们只考虑表 1 中提到的那些。

names = ['age','workclass','fnlwgt','education','education-num',
        'marital-status','occupation','relationship','race','sex',
        'capital-gain','capital-loss','hours-per-week','native-country',
        'y']

#Load dataset
df = pd.read_csv(data_path + 'adult_all.csv', names=names, na_values='?')
df = df.dropna()
df = df.apply(lambda x: x.str.strip() if x.dtype == 'object' else x)

print(len(df))
df.head(10)

---
	age	workclass	fnlwgt	education	education-num	marital-status	occupation	relationship	race	sex	capital-gain	capital-loss	hours-per-week	native-country	y
0	39	State-gov	77516	Bachelors	13	Never-married	Adm-clerical	Not-in-family	White	Male	2174	0	40	United-States	<=50K
...
9	42	Private	159449	Bachelors	13	Married-civ-spouse	Exec-managerial	Husband	White	Male	5178	0	40	United-States	>50K

算法公平性的探索性分析

评估公平性并不是在你拥有最终模型时开始的。它也应该是你探索性分析的一部分。一般来说，我们这样做是为了围绕我们的数据集建立一些直觉。因此，在建模时，你会对预期的结果有一个很好的了解。具体来说，为了公平起见，你需要了解数据的哪些方面可能导致不公平的模型。

由于[不公平的不同原因]³，你的模型可能会变得不公平。在我们的探索性分析中，我们将重点关注与数据相关的 3 个关键来源。这些是历史偏差、代理变量和不平衡数据集。我们希望了解这些因素在我们的数据中存在的程度。了解原因将有助于我们选择[解决不公平问题的最佳方法]⁴。

不平衡的数据集

我们首先要看看我们的数据集是否不平衡。具体来说，我们指的是敏感属性方面的不平衡。查看图 1，我们按种族和性别对人口进行了细分。你可以看到我们的数据集确实不平衡。第一张图表显示，85.4%的人口是白人。同样，66.9%的人口是男性。

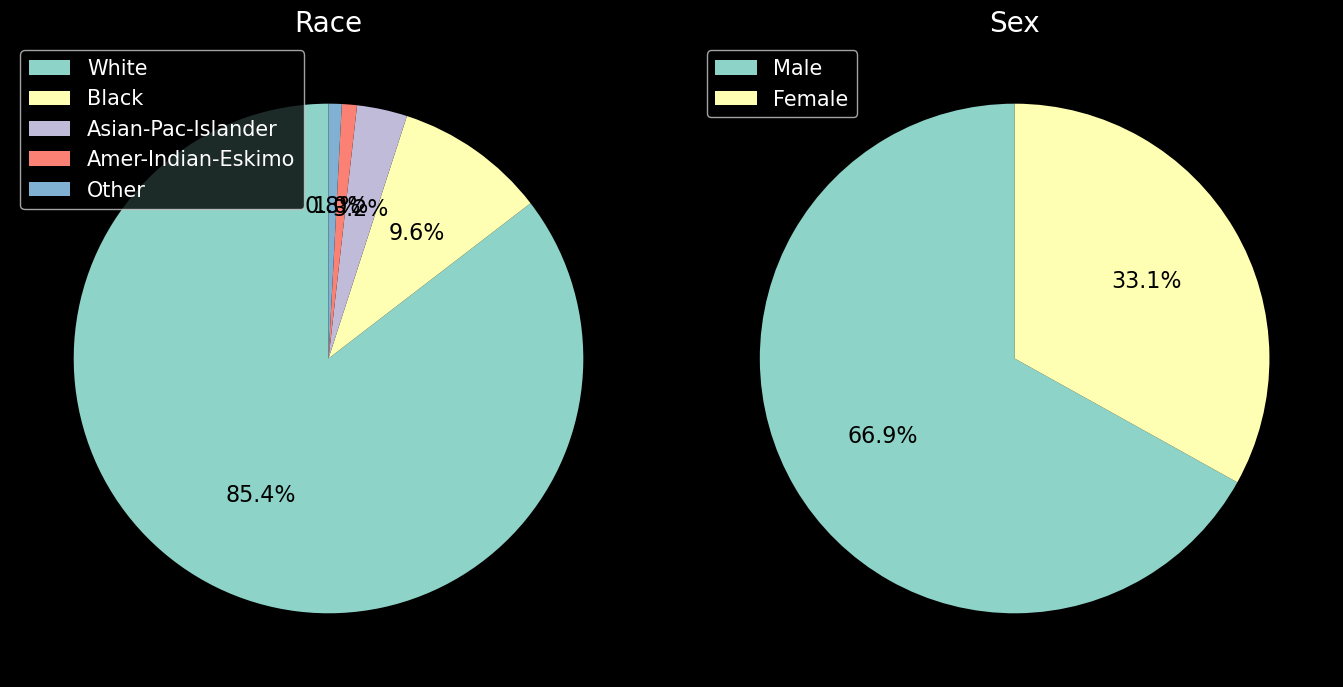
你可以在下面看到我们如何为种族属性创建饼图。我们首先按种族创建人口计数（第 2 行）。我们使用索引定义标签（第 3 行）。这些是我们在图 1 中看到的不同种族群体的名称。然后我们使用 matplotlib 中的 pie 函数绘制计数（第 6 行）。我们还使用标签创建图例（第 7 行）。性别属性饼图的代码非常相似。

# Get population count by race
counts = df['race'].value_counts()
labels = counts.index

# Plot pie chart
plt.pie(counts, startangle=90)
plt.legend(labels, loc=2,fontsize=15)
plt.title("Race",size=20)

数据集不平衡的问题在于模型参数可能会偏向多数。例如，女性和男性群体的趋势可能不同。趋势指的是特征和目标变量之间的关系。模型将尝试最大化整个群体的准确度。这样做可能会偏向男性群体的趋势。因此，我们对女性群体的准确度可能会较低。

定义受保护的特征

在继续之前，我们需要定义受保护的特征。我们通过使用敏感属性创建二进制变量来实现这一点。我们定义变量，以便 1 代表特权群体，0 代表非特权群体。通常，非特权群体在过去会面临历史不公正。换句话说，这个群体最有可能面临有偏见的模型做出的不公平决定。

我们使用以下代码定义这些特征。对于种族，我们定义受保护的特征，以便“白人”是特权群体（第 4 行）。也就是说，如果该人是白人，则变量的值为 1，否则为 0。对于性别，“男性”是特权群体（第 5 行）。接下来，我们将使用这些二进制变量代替原始敏感属性。

df_fair = df[['race','sex']].copy()

# Define protected features 
df_fair['priv_race'] = df_fair['race'].apply(lambda x: 1 if x=='White' else 0)
df_fair['priv_sex'] = df_fair['sex'].apply(lambda x: 1 if x=='Male' else 0)

# Define target variable 
df_fair['y'] = df['y'].apply(lambda x: 1 if x=='>50K' else 0)

df_fair.head()

---

race	sex	priv_race	priv_sex	y
0	White	Male	1	1	0
1	White	Male	1	1	0
2	White	Male	1	1	0
3	Black	Male	0	1	0
4	Black	Female	0	0	0

在上面的代码中，我们还定义了一个目标变量（第 8 行）。如果此人的收入高于 5 万美元，则其值为 1；如果此人的收入低于 5 万美元，则其值为 0。在第 1 行中，我们创建了具有原始敏感属性的df_fair 数据集。我们已将目标变量和受保护的特征添加到此数据集。它将用作剩余公平性分析的基础。

流行率

对于目标变量，流行率是阳性病例占总体病例的比例。当目标变量的值为 1 时，即为阳性病例。我们的数据集的总体流行率为24.1%。这意味着我们的数据集中大约有接近 1/4 的人收入超过 5 万美元。我们还可以使用流行率作为公平性指标。

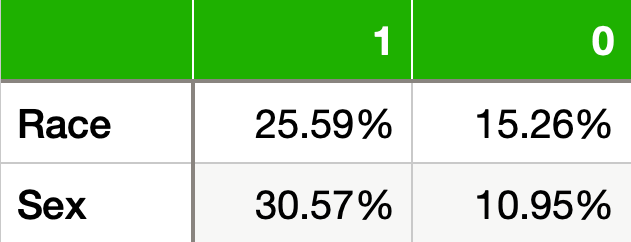
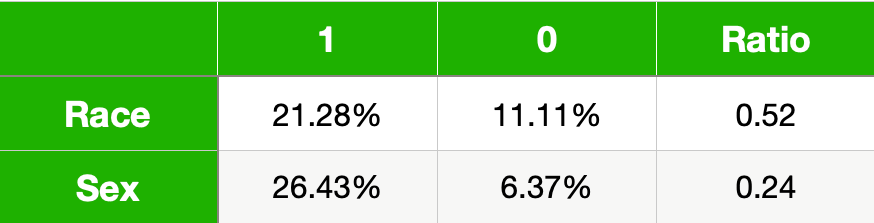
我们通过计算不同特权群体（1）和非特权群体（0）的流行率来做到这一点。你可以在下面的表 2 中看到这些值。请注意，特权群体的流行率要高得多。事实上，如果你是男性，那么收入超过 5 万美元的可能性几乎是女性的3 倍。

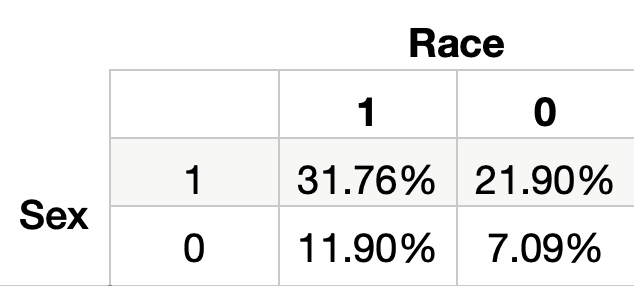
我们可以进一步计算受保护特征交集处的流行率。你可以在表 3中看到这些值。左上角给出了你同时属于两个特权群体（即性别 = 1 和种族 = 1）时的流行率。同样，右下角给出了你不属于任何特权群体（即性别 = 0 和种族 = 0）时的流行率。这告诉我们，白人男性收入超过 5 万美元的可能性是非白人女性的4 倍多。

我们使用下面的代码计算这些值。你可以看到，总体流行度只是目标变量的平均值（第 1 行）。同样，我们可以对不同的受保护特征组合取平均值（第 3-5 行）。

# Calculate prevelance
prev = df_fair['y'].mean()
prev_race = df_fair.groupby('priv_race')['y'].mean()
prev_sex = df_fair.groupby('priv_sex')['y'].mean()
prev_comb = df_fair.groupby(['priv_race','priv_sex'])['y'].mean()

此时，你应该问自己，为什么我们在流行率方面存在如此大的差异。该数据集是使用1994 年的美国人口普查数据构建的。该国有基于性别和种族的歧视历史。最终，目标变量反映了这种歧视。从这个意义上讲，流行率可用于了解历史不公正在我们的目标变量中所占的程度。

代理变量

分析潜在偏见来源的另一种方法是找到代理变量。这些是与我们的受保护特征高度相关或关联的模型特征。使用代理变量的模型可以有效地使用受保护特征来做出决策。

我们可以用类似于在特征选择过程中查找重要特征的方式来查找代理变量。也就是说，我们使用特征和目标变量之间的某种关联度量。只不过现在，我们使用受保护的特征而不是目标变量。我们将研究两种关联度量——相互信息和特征重要性。

在此之前，我们需要进行一些特征工程。我们首先像之前一样创建一个目标变量（第 2 行）。然后我们创建 6 个模型特征。首先，我们保留age、education-num和hours-per-week不变（第 5 行）。我们从marital-status和native-country创建二元特征（第 6-7 行）。最后，我们通过将原始职业分为 5 组来创建职业特征（第 9-16 行）。在下一节中，我们将使用这些相同的特征来构建我们的模型。

# Target variable 
y = df['y'].apply(lambda x:1 if x=='>50K' else 0)

# Model features
X = df[['age','education-num','hours-per-week']].copy()
X['marital-status'] = df['marital-status'].apply(lambda x:1 if x=='Married-civ-spouse' else 0)
X['native-country'] = df['native-country'].apply(lambda x:1 if x=='United-States' else 0) 

occ_groups = {
    'Priv-house-serv':0,'Other-service':0,'Handlers-cleaners':0,
    'Farming-fishing':1,'Machine-op-inspct':1,'Adm-clerical':1,
    'Transport-moving':2,'Craft-repair':2,'Sales':2,
    'Armed-Forces':3,'Tech-support':3,'Protective-serv':3,
    'Prof-specialty':4,'Exec-managerial':4, '?':-1}

X['occupation'] = [occ_groups[x] if x in occ_groups else -1 for x in df['occupation']]

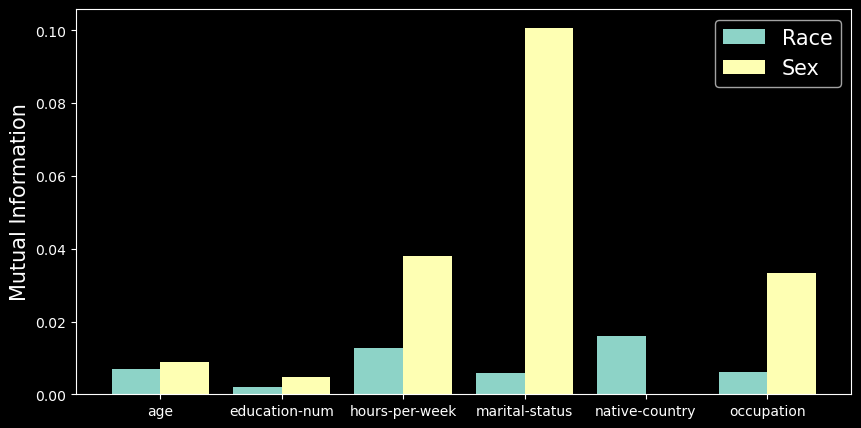
互信息是衡量两个变量之间非线性关联的指标。 它表示通过观察另一个变量，一个变量的不确定性降低了多少。 在图 2 中，您可以看到 6 个特征中每个特征与受保护特征之间的互信息值。 请注意，婚姻状况和性别之间的互信息值很高。 这表明这些变量之间可能存在关系。 换句话说，婚姻状况可能是性别的替代变量。

互信息是两个变量之间非线性关联的度量。它表示通过观察一个变量，一个变量的不确定性减少了多少。在图 2 中，你可以看到 6 个特征和受保护特征之间的互信息值。请注意婚姻状况和性别之间的高值。这表明这些变量之间可能存在关系。换句话说，婚姻状况可能是性别的代理变量。

我们使用下面的代码计算相互信息值。这是使用mutual_info_classif函数完成的。对于种族，我们传递特征矩阵（第 2 行）和种族保护特征（第 3 行）。我们还告诉函数 6 个特征中的哪些是离散的（第 4 行）。性别的代码类似（第 5 行）。

#Calculate mutual information
mut_race = mutual_info_classif(X,
                               df_fair['priv_race'],
                               discrete_features=[1,3,4,5])
mut_sex = mutual_info_classif(X,df_fair['priv_sex'],discrete_features=[1,3,4,5])

我们可以采取的另一种方法是使用受保护的特征构建模型。也就是说，我们尝试使用 6 个模型特征来预测受保护的特征。然后，我们可以使用该模型的特征重要性分数作为关联度量。你可以在图 3 中看到此过程的结果。

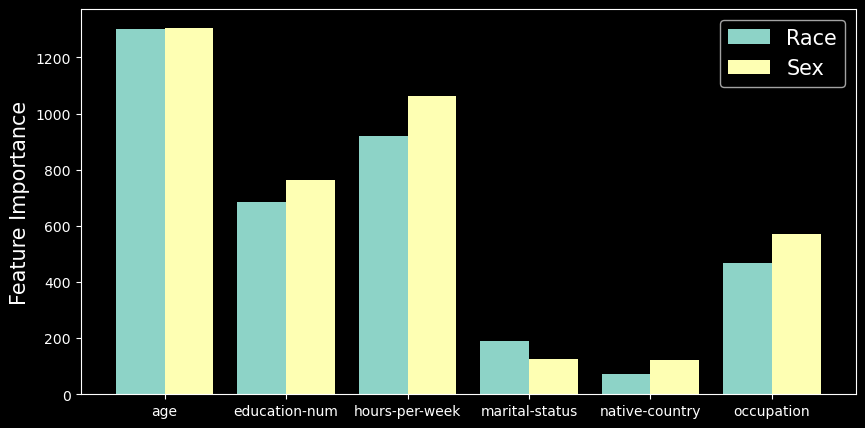
这个过程的另一个结果是我们得到了模型准确率。这些可以让我们衡量整体关联。预测种族的准确率为75.7% ，预测性别的准确率为79.4%。如果我们回到图 2 中的互信息值，这种差异是有道理的。你可以看到性别的值通常更高。最终，我们可以预期代理变量对性别的影响比对种族的影响更大。

你可以在下面看到我们如何计算种族指标。我们首先获取一个平衡样本（第 2-7 行）。这样我们的数据集中就有相同数量的特权和非特权。然后我们使用此数据集构建模型（第 10-11 行）。请注意，我们使用种族保护功能作为目标变量。然后我们获得模型预测（第 12 行），计算准确率（第 15 行）并获得特征重要性分数（第 18 行）。

# Get balanced sample 
y_race_0 = df_fair[df_fair['priv_race'] == 0]['priv_race']
y_race_1 = df_fair[df_fair['priv_race'] == 1]['priv_race']
y_race_1 = y_race_1.sample(len(y_race_0))
y_race = pd.concat([y_race_0,y_race_1])

X_race = X.loc[y_race.index]

# Train model and get predictions
model = xgb.XGBClassifier(objective="binary:logistic")
model.fit(X_race, y_race)
y_pred = model.predict(X_race)

# Calculate accuracy 
acc_race = accuracy_score(y_race, y_pred)

# Get feature importance 
fi_race = model.get_booster().get_score(importance_type='weight')

因此，我们已经看到数据集是不平衡的，特权群体的流行率更高。我们还发现了一些潜在的代理变量。但是，这种分析并没有告诉我们我们的模型是否会不公平。它只是强调了可能导致不公平模型的问题。在接下来的部分中，我们将建立一个模型并表明其预测是不公平的。最后，我们将回顾这一探索性分析。我们将看到它如何帮助解释导致不公平预测的原因。

造型

我们使用下面的代码构建模型。我们使用 XGBClassfier 函数（第 2 行）。我们使用之前在代理变量部分定义的特征和目标变量训练模型。然后我们得到预测（第 6 行）并将它们添加到我们的 df_fair 数据集（第 7 行）。最后，该模型的准确率为 85%。精确率为 74%，召回率为 61%。我们现在想衡量这些预测的公平性。

# Train model 
model = xgb.XGBClassifier(objective="binary:logistic")
model.fit(X, y)

# Get predictions
y_pred = model.predict(X)
df_fair['y_pred'] = y_pred

在我们继续之前，如果你愿意，可以用自己的模型替换此模型。或者你可以尝试不同的模型特征。这是因为我们将使用的所有公平性措施都是[模型无关的]⁵。这意味着它们可以与任何模型一起使用。它们的工作原理是将预测与原始目标变量进行比较。最终，你将能够在大多数应用程序中应用这些指标。

公平的定义

我们通过应用不同的公平定义来衡量公平性。大多数定义都涉及将人群分为特权群体和非特权群体。然后，你可以使用某些指标（例如准确率、FPR、FNR）比较这些群体。我们将看到，最佳指标显示谁从模型中受益。

通常，模型的预测要么给某人带来好处，要么不带来好处。例如，银行模型可以预测某人不会拖欠贷款。这将带来获得贷款的好处。另一个好处的例子可能是收到工作机会。对于我们的模型，我们假设 Y = 1 将带来好处。也就是说，如果模型预测该人的收入超过 5 万美元，他们将以某种方式受益。

准确性

首先，让我们讨论一下准确度，以及为什么它不是公平性的理想衡量标准。我们可以基于图 4中的混淆矩阵来计算准确度。这是一个标准的混淆矩阵，用于将模型预测与实际目标变量进行比较。这里 Y = 1 是正预测，Y=0 是负预测。在计算其他公平性指标时，我们也将参考这个矩阵。

查看图 5，你可以看到我们如何使用混淆矩阵来计算准确度。准确度是真阴性和真阳性的数量除以总观察次数。换句话说，准确度是正确预测的百分比。

表 4 给出了我们模型受保护特征的准确率。比例列给出了非特权 (0) 到特权 (1) 的准确率。对于两个受保护的特征，你可以看到非特权组的准确率实际上更高。这些结果可能会误导你相信该模型正在使非特权组受益。

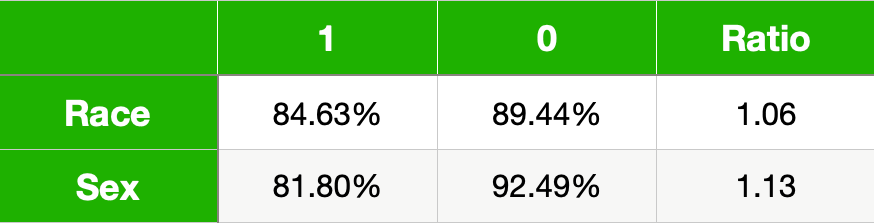
问题在于，准确率可能会掩盖模型的后果。例如，错误的正向预测 (FP) 会降低准确率。但是，该人仍会从此预测中受益。例如，即使预测不正确，他们仍会收到贷款或工作机会。

机会均等（真实阳性率）

为了更好地体现模型的优势，我们可以使用真实阳性率 (TPR)。你可以在图 6 中看到我们如何计算 TPR。分母是实际阳性的数量。分子是正确预测的阳性的数量。换句话说，TPR 是被正确预测为阳性的实际阳性的百分比。

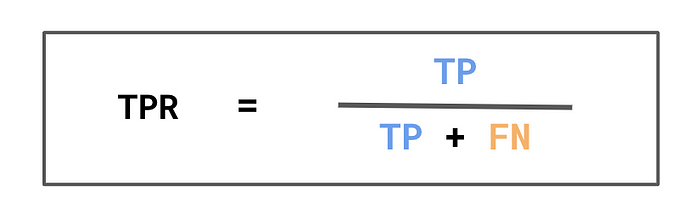
请记住，我们假设积极的预测会带来一些好处。这意味着分母可以看作应该从模型中受益的人数。分子是应该和已经受益的人数。因此，TPR 可以解释为从模型中正确受益的人数百分比。

例如，假设一个贷款模型，其中 Y=1 表示客户没有违约。分母是没有违约的人数。分子是没有违约的人数，我们预测他们不会违约。这意味着 TPR 是我们向其提供贷款的优质客户的百分比。对于招聘模型，它将被解释为收到工作邀请的优质候选人的百分比。

表 5 给出了我们模型的 TPR。同样，该比率给出了无特权 (0) 到有特权 (1) 的 TPR。与准确度相比，你可以看到无特权群体的 TPR 较低。这表明无特权群体中从该模型中受益的比例较小。也就是说，正确预测高收入者收入较高的比例较小。

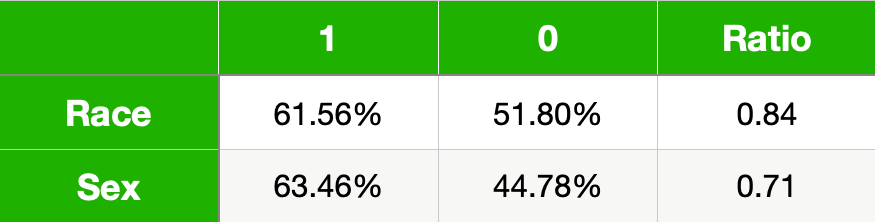
与流行率一样，我们可以进一步找到受保护特征交集处的 TPR。请注意，当一个人同时处于非特权群体中时，TPR 甚至更低。事实上，白人男性的 TPR 比非白人女性高出 50% 以上。

使用 TPR 可以让我们得到公式 1中对公平的第一个定义。在平等机会下，如果特权群体和非特权群体的 TPR 相等，我们认为该模型是公平的。在实践中，我们会为统计不确定性留出一些余地。我们可以要求差异小于某个截止值（公式 2）。在我们的分析中，我们采用了比率。在这种情况下，我们要求比率大于某个截止值（公式 3）。这确保了非特权群体的 TPR 不会明显小于特权群体的 TPR。

问题是我们应该使用什么截止值？实际上，这个问题没有好的答案。这取决于你的行业和应用。如果你的模型具有重大影响，例如抵押贷款申请，你将需要更严格的截止值。截止值甚至可能由法律定义。无论哪种方式，在衡量公平性之前定义截止值都很重要。

假阴性率

在某些情况下，你可能希望捕捉模型的负面后果。你可以使用图 8 中所示的 FNR 来做到这一点。同样，分母给出实际正数的数量。只不过现在我们将错误预测的负数的数量作为分子。换句话说，FNR 是错误预测为负数的实际正数的百分比。

FNR 可以解释为错误地未从模型中受益的人的百分比。例如，它可能是应该获得但未获得贷款的客户的百分比。对于我们的模型，它是被预测为低收入的高收入者的百分比。

你可以在表 7 中看到我们模型的 FNR 。现在，弱势群体的 FNR 更高。换句话说，特权群体中没有得到好处的比例更高。从这个意义上讲，我们得出的结论与使用均等赔率的 TPR 时类似。也就是说，该模型似乎对弱势群体不公平。

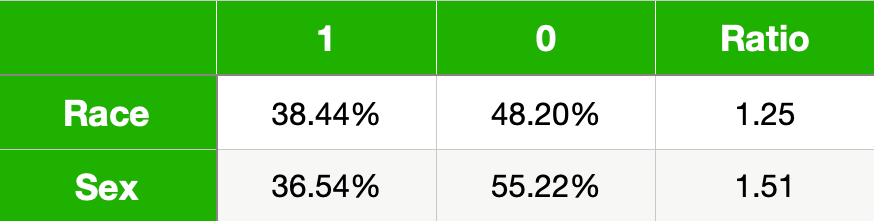
事实上，要求 FNR 相等将给我们提供与平等机会相同的定义。这是因为公式 1中看到的线性关系。换句话说，相等的 TPR 意味着我们也拥有相等的 FNR。你应该记住，我们现在要求该比率小于某个截止值（公式 2）。

使用 FNR 定义平等机会似乎没有必要。但是，在某些情况下，使用负面后果来定义公平性可以更好地阐明你的观点。例如，假设我们建立一个模型来预测皮肤癌。FNR 将给出患有癌症但未被诊断出患有癌症的人的百分比。这些错误可能会致命。最终，以这种方式定义公平性可以更好地凸显不公平模型的后果。

均等赔率

我们可以通过查看假阳性率 (FPR) 来获取模型的优势。如图10所示，分母是实际阴性的数量。这意味着 FPR 是被错误预测为阳性的实际阴性的百分比。这可以解释为从模型中错误获益的人的百分比。例如，它将是收到工作机会的不合格人员的百分比。

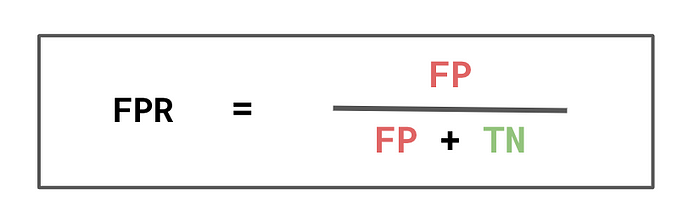
对于我们的模型，FPR 会给出预测为高收入的低收入者的数量。你可以在表 8 中看到这些值。我们再次得到特权群体的更高比率。这告诉我们，特权群体中更高比例的人从该模型中不当获益。

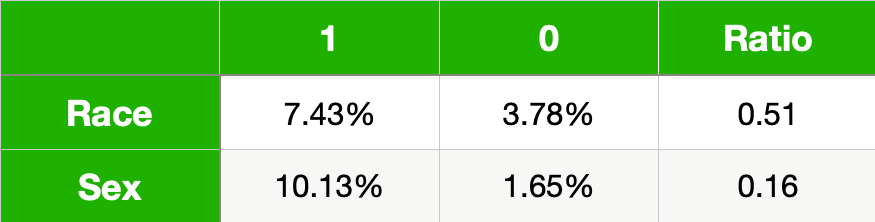
这引出了公平的第二个定义，即均等机会。与平等机会一样，此定义要求 TPR 相等。现在我们还要求 FPR 相等。这意味着均等机会 可以被视为公平的更严格定义。为了使模型公平，总体利益应该相等，这也是有道理的。也就是说，应该有相似比例的群体既合法又非法地受益。

均等化几率的一个优点是，我们如何定义目标变量并不重要。假设 Y = 0 会带来好处。在这种情况下，TPR 和 FPR 的解释互换。TPR 现在捕获错误的利益，而 FPR 现在捕获正确的利益。均等化几率已经使用了这两个比率，因此解释保持不变。相比之下，平等机会的解释发生了变化，因为它只考虑 TPR。

不同影响

我们对公平性的最后一个定义是差异影响(DI)。我们首先计算图 12 所示的 PPP 率。这是被正确 (TP) 或错误 (FP) 预测为阳性的人的百分比。我们可以将其解释为将从模型中受益的人的百分比。

对于我们的模型，它是我们预测高收入人群的百分比。你可以在表 9 中看到这些值。同样，这些数字表明该模型对弱势群体不公平。也就是说，他们中只有较小比例的人从该模型中受益。不过，在解释这些值时，我们应该考虑这个定义的一个缺点。我们将在本节末尾讨论这个问题。

在DI下，如果我们有相等的 PPP 率（公式 1） ，我们认为一个模型是公平的。同样，在实践中，我们使用截止值来留出一些余地。这个定义应该代表不同影响的法律概念。在美国，有一个法律先例将截止值设置为0.8。也就是说，弱势群体的 PPP 不得低于弱势群体的 PPP 的 80% 。

DI 的问题在于它没有考虑到基本事实。回想一下探索性分析中的流行率值。我们发现这些值存在偏差。特权群体的值较高。对于一个完全准确的模型，我们不会有假阳性。这意味着流行率将与不同影响率相同。换句话说，即使对于一个完全准确的模型，我们的不同影响率仍可能较低。

在某些情况下，期望流行率或 DI 相等可能是合理的。例如，我们期望模型预测男性和女性成为工作优质候选人的比例相等。在其他情况下，这没有意义。例如，肤色较浅的人更容易患皮肤癌。我们预计肤色较浅的人患皮肤癌的几率更高。在这种情况下，低 DI 比率并不表示模型不公平。

公平性定义代码

我们使用fairness_metrics函数来获取上述所有结果。该函数采用包含实际 (y) 和预测目标值 (y_pred) 的 DataFrame。它使用这些值创建混淆矩阵（第 5 行）。该矩阵具有我们在图 4 中看到的 4 个值。我们获取这 4 个值（第 6 行）并使用它们来计算公平性指标（第 8-13 行）。然后我们将这些指标作为数组返回（第 15 行）。

def fairness_metrics(df):
    """Calculate fairness for subgroup of population"""
    
    # Confusion Matrix
    cm=confusion_matrix(df['y'],df['y_pred'])
    TN, FP, FN, TP = cm.ravel()
    
    N = TP+FP+FN+TN # Total population
    ACC = (TP+TN)/N # Accuracy
    TPR = TP/(TP+FN) # True positive rate
    FPR = FP/(FP+TN) # False positive rate
    FNR = FN/(TP+FN) # False negative rate
    PPP = (TP + FP)/N # % predicted as positive
    
    return np.array([ACC, TPR, FPR, FNR, PPP])  

你可以在下面看到我们如何将此函数用于种族保护功能。我们首先将人口的子组传递给fairness_metrics函数。具体来说，我们获取特权组（第 2 行）和非特权组（第 3 行）的指标。然后，我们可以获取非特权组与特权组指标的比率（第 6 行）。

# Calculate fairness metrics for race
fm_race_1 = fairness_metrics(df_fair[df_fair.priv_race==1])
fm_race_0 = fairness_metrics(df_fair[df_fair.priv_race==0])

# Get ratio of fairness metrics
fm_race = fm_race_0/fm_race_1

我们的模型为何有偏差？

根据公平的不同定义，我们发现我们的模型对弱势群体不公平。然而，这些定义并没有告诉我们为什么我们的模型不公平。要做到这一点，我们需要做进一步的分析。一个好的起点是回到我们最初的探索性分析。

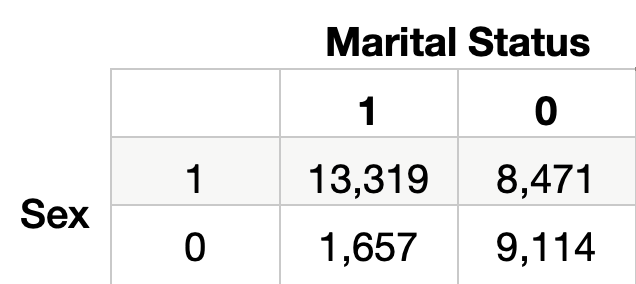
例如，使用相互信息，我们发现婚姻状况是性别的潜在代理变量。我们可以通过查看表 10 中的细分来开始理解为什么会这样。请记住，婚姻状况 = 1 表示该人已婚。我们可以看到 62% 的男性已婚。而人口中只有 15% 的女性已婚。

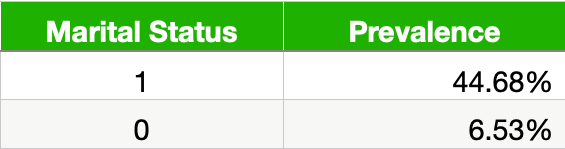
在表 11 中，我们可以看到已婚人士的流行率高出 6 倍以上。模型将在进行预测时使用这种关系。也就是说，它更有可能预测已婚人士的收入超过 5 万美元。问题是，正如我们上面所看到的，这些已婚人士中的大多数都是男性。换句话说，女性结婚的可能性较小，因此模型不太可能预测她们的收入超过 5 万美元。

最后，要充分解释模型不公平的原因，还有更多工作要做。在这样做时，我们需要考虑不公平的所有潜在原因。我们在本文中谈到了一些原因。你也可以在下面的第一篇文章中深入了解它们。下一步是纠正不公平。我们将在以后的文章中研究定量和非定量方法。

---

---

1. Github, https://github.com/hivandu/public_articles/blob/main/src/algorithm%20fairness/Measuring%20Bias.ipynb↩︎

2. 数据集, https://archive.ics.uci.edu/ml/datasets/adult↩︎

3. 不公平的原因，将在之后的文章中详细分析。↩︎

4. 解决不公平问题的最佳方法, 也将在日后文章中详细描述。↩︎

5. 模型无关, 日后文章中描述↩︎