发表AI

特征工程的力量

原文：The Power of Feature Engineering

为什么你应该使用逻辑回归来建模非线性决策边界（使用 Python 代码）

作为一名大数据从业者，复杂的机器学习技术非常具有吸引力。使用一些深度神经网络 (DNN) 获得额外的 1% 准确率，并在此过程中启动 GPU 实例，这让人非常满意。然而，这些技术通常将思考留给计算机，让我们对模型的工作原理了解甚少。所以，我想回到基础知识。

img

在本文中，我希望教你一些关于特征工程的知识，以及如何使用它来建模非线性决策边界。我们将探讨两种技术的优缺点：逻辑回归（带有特征工程）和 NN 分类器。将提供用于拟合这些模型以及可视化其决策边界的 Python 代码。你可以在 Github1 上找到完整的项目代码。最后，我希望让你理解为什么特征工程可能是其他非线性建模技术的更好替代方案。

什么是特征工程

当你从原始数据创建特征或将现有特征的函数添加到数据集时，你就在进行特征工程。这通常使用特定领域的领域知识来完成2。例如，假设我们想要预测一个人从手术中恢复所需的时间（Y）。从之前的手术中，我们获得了患者的康复时间、身高和体重。根据这些数据，我们还可以计算出每个患者的 BMI = 身高/体重²。通过计算 BMI 并将其纳入数据集，我们正在进行特征工程。

我们为什么要进行特征工程

特征工程非常强大，因为它允许我们将非线性问题重新表述为线性问题。为了说明这一点，假设恢复时间与身高和体重有以下关系：

\[ Y = \beta_0 + \beta_1（高度）+ \beta_2（重量）+ \beta_3（高度/重量^2）+ 噪声 \]

查看第 3 项，我们可以看到 Y 与身高和体重没有线性关系。这意味着我们可能不会期望线性模型（例如线性回归）能够很好地估计 β 系数。你可以尝试使用非线性模型（例如 DNN），或者我们可以通过进行一些特征工程来帮助我们的模型。如果我们决定将 BMI 作为一个特征，则关系将变为：

\[ Y = \beta_0 + \beta_1（高度）+ \beta_2（重量）+ \beta_3（BMI）+ 噪声 \] Y 现在可以被建模为 3 个变量的线性关系。因此，我们期望线性回归能够更好地估计系数。稍后，我们将看到同样的想法也适用于分类问题。

为什么不让电脑来做这项工作

如果从技术角度来讲，特征工程本质上就是核心技巧，因为我们将特征映射到更高的平面3。尽管使用核技巧通常不需要太多思考。核函数被视为超参数，可以使用蛮力找到最佳函数——尝试大量不同的函数变体。使用正确的核函数，你可以建模非线性关系。给定正确数量的隐藏层 / 节点，DNN 还将自动构建特征的非线性函数4。那么，如果这些方法可以建模非线性关系，我们为什么还要费心进行特征工程呢？

我们上面解释了特征工程如何让我们即使在使用线性模型的情况下也能捕捉数据中的非线性关系。这意味着，根据问题的不同，我们可以实现与非线性模型类似的性能。我们将在本文后面详细介绍一个示例。除此之外，使用特征工程还有其他好处，这使得这项技术很有价值。

img

首先，你会更好地理解模型的工作原理。这是因为你确切地知道模型使用什么信息进行预测。此外，像逻辑回归这样的模型可以通过直接查看特征系数来轻松解释。第二个原因与第一个原因相符，即模型更容易解释。如果你在工业界工作，这一点尤其重要。你的同事也更有可能接触到一些更简单的模型。第三个原因是你的模型不太可能过度拟合训练数据。通过强制加载不同的超参数，很容易导致对数据中噪声建模。相比之下，有了深思熟虑的特征，你的模型将是直观的，并且很可能模拟真实的潜在趋势。

数据集

让我们深入研究一个实际的例子。为了尽可能清晰，我们将使用人工生成的数据集。为了避免这个例子太枯燥，我们将围绕它创建一个叙述。假设你的人力资源部门要求你创建一个模型来预测员工是否会晋升。该模型应该考虑员工的年龄和绩效分数。

我们在下面的代码中为 2000 名假设员工创建特征。员工的年龄可以在 18 到 60 岁之间。绩效分数可以在 -10 到 10 之间（10 为最高）。这两个特征都经过了打乱，因此它们不相关。然后我们使用以下年龄 (a) 和绩效 (p) 函数来生成目标变量：

\[ \gamma（a，p）= 100（a）+ 200（p）+ 500（a / p）- 10000 + 500（noise） \]

当 \(\gamma(a,p)≥ 0\) 时，员工会得到晋升；当 $(a,p) < 0 $​时，员工不会得到晋升。我们可以看到，上面的函数中包含了 a/p 项。这意味着决策边界将不是年龄和绩效的线性函数。还包括随机噪声，因此数据不是完全可分离的。换句话说，模型不可能 100% 准确。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import numpy as np
import pandas as pd

n_points = 2000

age = np.round(np.linspace(18, 60, n_points), 2) # age of employee
np.random.shuffle(age) # shuffle

performance = np.linspace(-10, 10, n_points) # performance score of employee
np.random.shuffle(performance) # shuffle

noise = np.random.randn(n_points)

g = (100 * age) + 200 * (performance) + 500 * age / performance - 10000 + 500 * noise
y = [1 if y >= 0 else 0 for y in g]

data = pd.DataFrame(data = {'age': age, 'performance': performance, 'y': y})

print(sum(y))
data.head()

---
474
	age		performance	y
0	53.32	-6.098049	0
1	32.10	-7.848924	0
2	58.72	9.709855	1
3	59.52	4.387194	1
4	28.55	7.418709	0

如果上述步骤有点令人困惑，请不要担心。我们可以通过使用以下代码可视化数据集来使事情变得更清晰。在这里，我们创建了数据的散点图，结果可以在图 1 中看到。仅通过两个特征，很容易准确地看到发生了什么。在 y 轴上，我们有员工的绩效分数，在 x 轴上，我们有员工的年龄。晋升员工的分数为红色，未晋升的员工分数为蓝色。最终，2000 名员工中有 459 名（23％）获得了晋升。对于不同的随机样本，该比例会略有变化。

1
2
3
4
5
6
7
8
9
10
plt.subplots(nrows = 1, ncols = 1, figsize = (15, 10))

plt.scatter('age', 'performance', c = '#ff2121', s = 50, edgecolors = '#000000', data = data[data.y == 1])
plt.scatter('age', 'performance', c = '#2176ff', s = 50, edgecolors = '#000000', data = data[data.y == 0])
plt.ylabel('Performance Score', size = 20)
plt.xlabel('Age', size = 20)
plt.yticks(size = 12)
plt.xticks(size = 12)
plt.legend(['Promoted', 'Not Promoted'], loc = 2, prop = {'size': 20})
plt.savefig('../figures/article_feature_eng/figure1.png', format = 'png')

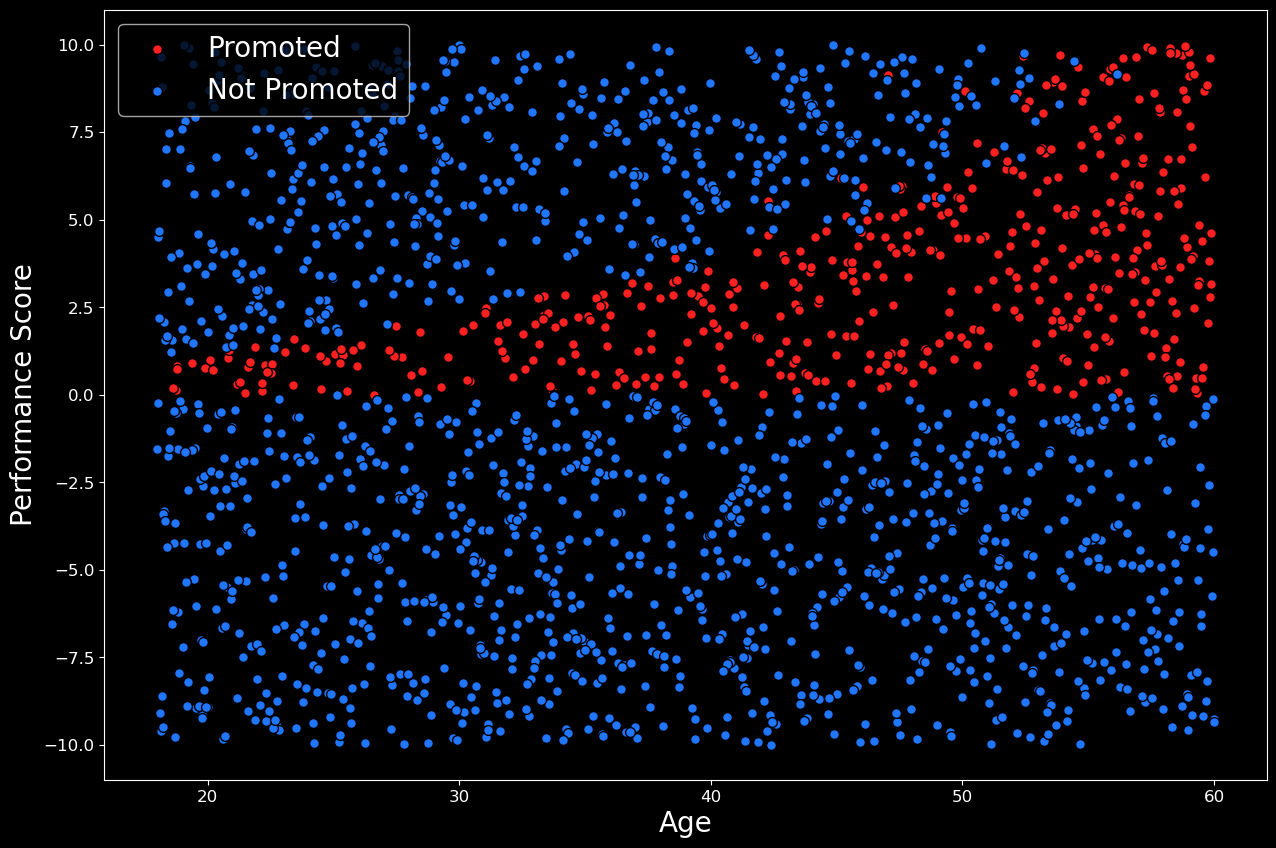
图 1：数据散点图

尽管这些数据是生成的，但我们仍然可以对该图做出现实的解释。在图 1 中，我们可以看到 3 个不同的员工组。第一个是绩效得分低于 0 的组。由于绩效不佳，这些员工中的大多数都没有得到晋升，我们还可以预期其中一些员工被解雇。我们可以预期得分高于 0 的员工要么得到晋升，要么接受其他公司的报价。得分特别高的员工往往会离开。这可能是因为他们的需求量很大，而且在其他地方得到了更好的报价。然而，随着雇主年龄的增长，他们需要更高的绩效分数才能离开。这可能是因为年长的员工在目前的职位上更舒服。

无论如何，很明显，决策边界不是线性的。换句话说，不可能画出一条直线来很好地区分晋升组和未晋升组。因此，我们不会指望线性模型能做得很好。让我们通过尝试仅使用两个特征（年龄和表现）来拟合逻辑回归模型来证明这一点。

逻辑回归

在下面的代码中，我们将 2000 名员工分成训练集（70%）和测试集（30%）。我们使用训练集来训练逻辑回归模型。然后，使用该模型，我们对测试集进行预测。测试集的准确率为 82%。这似乎不算太糟糕，但我们应该考虑到只有不到 23% 的员工获得了晋升。因此，如果我们只是猜测没有员工会得到晋升，那么我们应该预期准确率约为 77%。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from sklearn.model_selection import train_test_split
import sklearn.metrics as metric
import statsmodels.api as sm

x = data[['age', 'performance']]
x = sm.add_constant(x)
y = data['y']
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3, random_state = 2024)

model = sm.Logit(y_train, x_train).fit() # fit logistic regression model

predictions = np.around(model.predict(x_test))
accuracy = metric.accuracy_score(y_test, predictions)

print(round(accuracy * 100, 2))

---
Optimization terminated successfully.
         Current function value: 0.428402
         Iterations 7
81.83

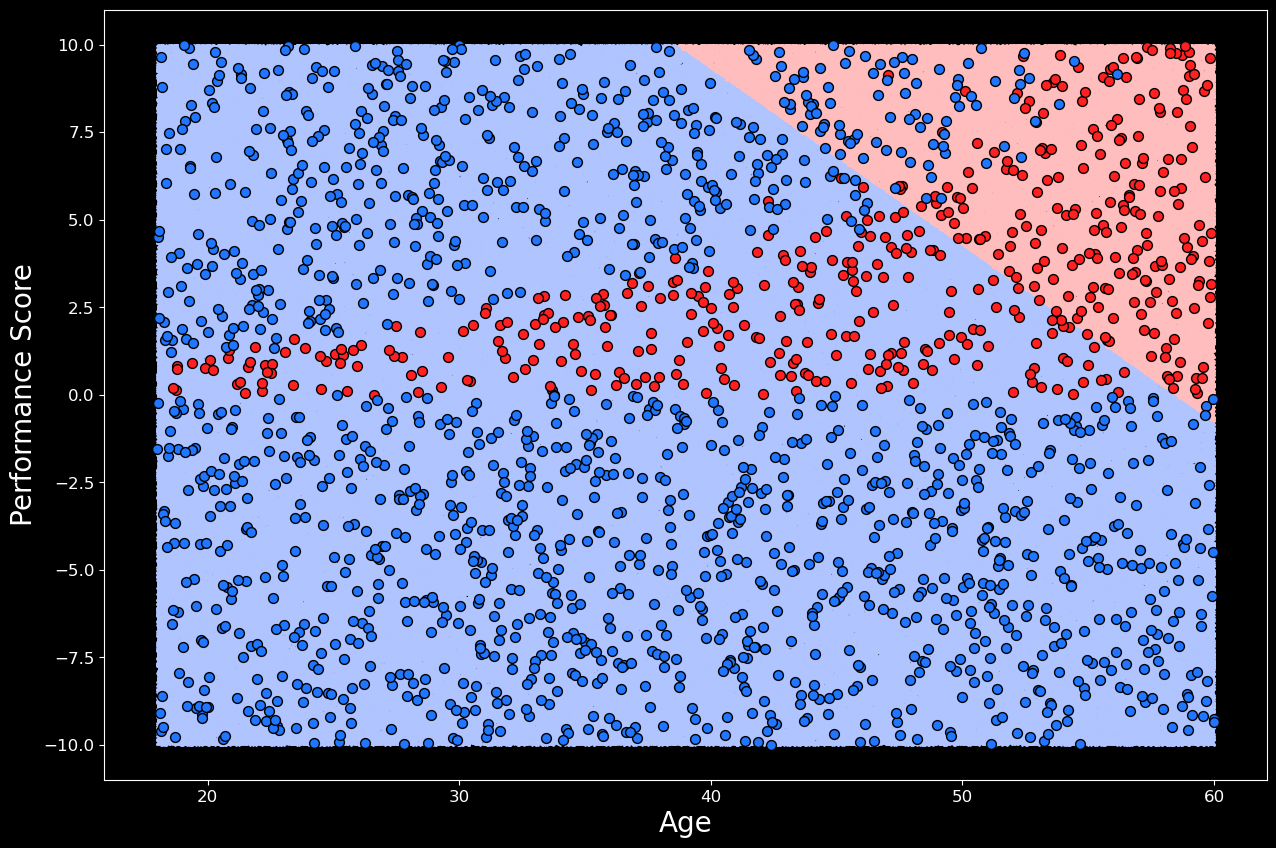
通过使用以下代码可视化决策边界，我们可以更好地理解模型正在做什么。在这里，我们在样本空间内生成一百万个点。然后，我们使用逻辑回归模型对所有这些点进行预测。与图 1 中的散点图一样，我们可以绘制每个点。每个点的颜色由模型的预测决定 — 如果模型预测晋升，则为粉红色，否则为浅蓝色。这为我们提供了决策边界的良好近似值，可以在图 2 中看到。然后，我们可以在这些点上绘制实际数据集。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
n_points = 1000000 # use many point to visualise decision boundry

age_db = np.linspace(18, 60, n_points)
np.random.shuffle(age_db)

performance_db = np.linspace(-10, 10, n_points)
np.random.shuffle(performance_db)

data_db = pd.DataFrame({'age': age_db, 'performance': performance_db})
data_db = sm.add_constant(data_db)

# make predictions on the decision boundry points
predictions = model.predict(data_db)
y_db = [round(p) for p in predictions]
data_db['y'] = y_db

fig, ax = plt.subplots(nrows = 1, ncols = 1, figsize = (15, 10))

# Plot decision boundry
plt.scatter('age', 'performance', c = '#ffbdbd', s = 1, data = data_db[data_db.y == 1])
plt.scatter('age', 'performance', c = '#b0c4ff', s = 1, data = data_db[data_db.y == 0])

# Plot employee data points
plt.scatter('age', 'performance', c = '#ff2121', s = 50, edgecolors = '#000000', data = data[data.y == 1])
plt.scatter('age', 'performance', c = '#2176ff', s = 50, edgecolors = '#000000', data = data[data.y == 0])
plt.ylabel('Performance Score', size = 20)
plt.xlabel('Age', size = 20)
plt.yticks(size = 12)
plt.xticks(size = 12)

plt.savefig('../figures/article_feature_eng/figure2.png', format = 'png')

从决策边界来看，我们可以看到模型表现很糟糕。它预测会升职的员工中，大约有一半没有升职。然后，对于大多数获得晋升的员工，它预测他们没有获得晋升。请注意，决策边界是一条直线。这强调了逻辑回归是一个线性分类器。换句话说，该模型只能构建一个决策边界，它是你赋予它的特征的线性函数。此时，我们可能会想尝试不同的模型，但让我们看看是否可以使用特征工程来提高性能。

图2：逻辑回归模型的决策边界

具有特征工程的逻辑回归

首先，如下面的代码所示，我们添加了附加特征（即年龄与表现的比率）。从那时起，我们遵循与之前的模型相同的过程。训练测试分割是相同的，因为我们对 “random_state” 使用相同的值。最后，这个模型的准确率达到了 98%，这是一个显着的改进。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
data['age_perf_ratio'] = age / performance

x = data[['age', 'performance', 'age_perf_ratio']]
x = sm.add_constant(x)
y = data['y']

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3, random_state = 2024)

model = sm.Logit(y_train, x_train).fit() # fit new logistic regression model

predictions = np.around(model.predict(x_test))
accuracy = metric.accuracy_score(y_test, predictions)

print(round(accuracy * 100, 2))

---
Optimization terminated successfully.
         Current function value: 0.039001
         Iterations 17
98.17

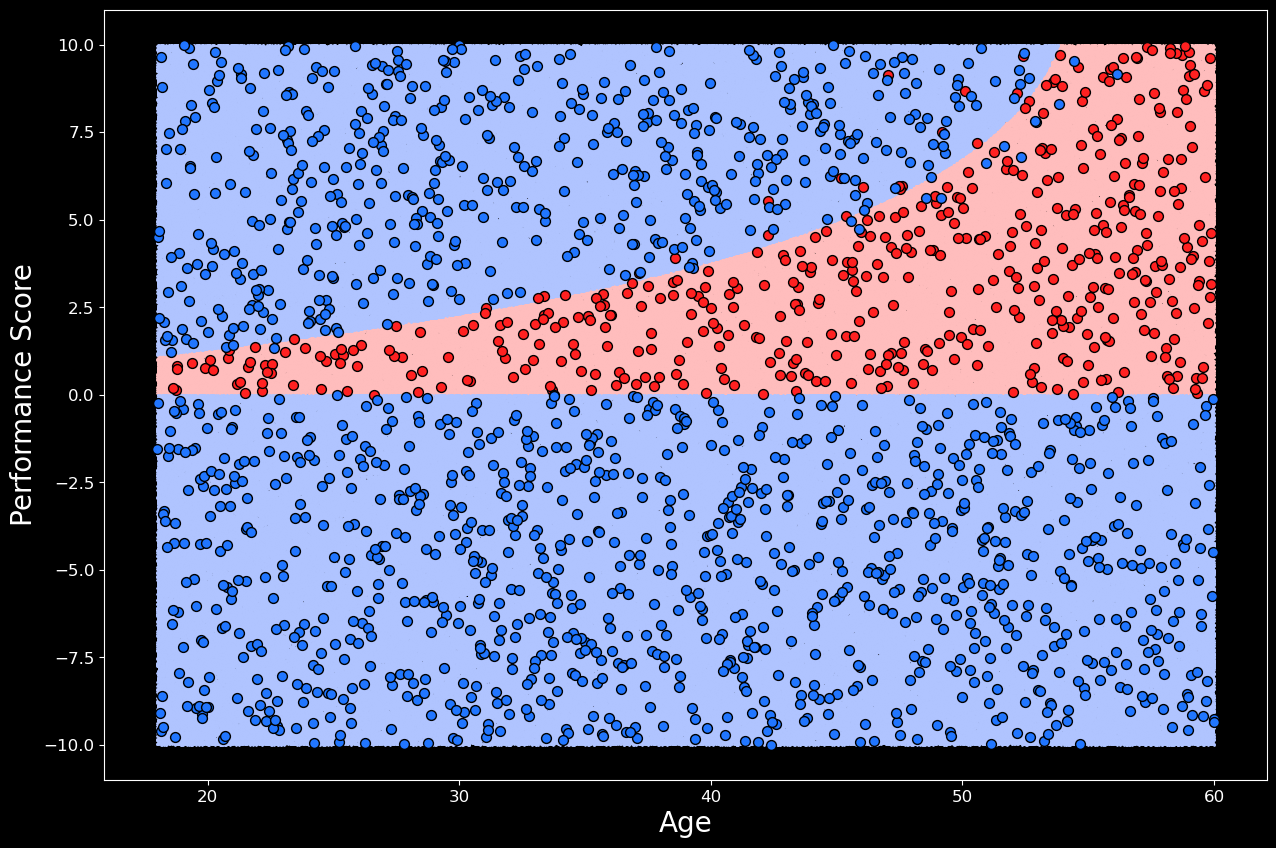
该模型仍然只需要员工的年龄和绩效即可进行预测。这是因为附加特征是年龄和绩效的函数。这使我们能够以与以前相同的方式可视化决策边界。即通过在样本空间中的每个年龄-绩效点使用模型的预测。我们可以看到，在图 3 中，通过添加附加特征，逻辑回归模型能够对非线性决策边界进行建模。从技术上讲，这是年龄和绩效的非线性函数，但它仍然是所有 3 个特征的线性函数。

图 3：具有特征工程的逻辑回归模型的决策边界

使用逻辑回归的另一个好处是模型是可解释的。这意味着模型可以用人类的术语来解释5。换句话说，我们可以直接查看模型系数来了解其工作原理。我们可以在表 1 中看到模型特征的系数及其 p 值。我们不会讲得太详细，但系数可以让你根据晋升几率的变化来解释特征的变化6。如果特征具有正系数，则该特征值的增加会导致晋升几率的增加。

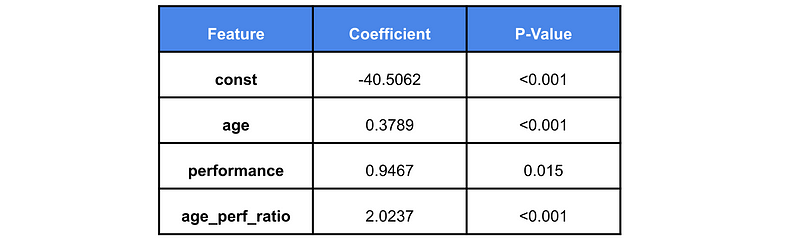
表1：逻辑回归模型摘要

从表 1 可以看出，随着年龄的增长，获得晋升的可能性也会增加。另一方面，对于绩效，这种关系并不那么明显。绩效的提高也会降低年龄/绩效比率。这意味着，绩效提高对几率的影响取决于员工的年龄。这非常符合直觉，因为它与我们在散点图中看到的一致。在这种情况下，可能没有必要使用系数以这种方式解释模型。仅仅可视化决策边界就足够了，但是，随着我们增加特征数量，这样做变得更加困难。在这种情况下，模型系数是理解模型如何工作的重要工具。

同样，P 值也有助于我们对模型的理解。由于系数是统计估计值，因此具有一定的不确定性。换句话说，我们可以确定系数要么是正值，要么是负值。这一点非常重要，因为如果我们不能确定系数的符号，就很难用几率的变化来解释特征的变化。从表 1 中我们可以看出，所有系数在统计意义上都是显著的。这并不奇怪，因为我们是利用特征函数生成数据的。

总体而言，当我们生成数据时，上述分析非常简单。因为我们知道使用什么函数来生成数据，所以很明显，附加特征会提高模型的准确性。实际上，事情不会这么简单。如果你对数据没有很好的理解，你可能需要与人力资源部门的某个人交谈。他们可能会告诉你他们过去看到的任何趋势。否则，通过使用各种图表和汇总统计数据探索该数据，你可以了解哪些特征可能很重要。但是，假设我们不想做所有这些艰苦的工作。

神经网络

为了进行比较，我们使用非线性模型。在下面的代码中，我们使用 Keras 来拟合 NN。我们仅使用年龄和表现作为特征，因此 NN 的输入层的维度为 2。有 2 个隐藏层，分别有 20 个和 15 个节点。两个隐藏层都具有 relu 激活函数，输出层具有 sigmoid 激活函数。为了训练模型，我们使用 10 和 100 个 epoch 的批处理大小。训练集大小为 1400，这给了我们 14000 个步骤。最后，该模型在测试集上的准确率达到了 96%。这与逻辑回归模型的准确率略低，但是也相差不大，不过我们不必进行任何特征工程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from keras.models import Sequential
from keras.layers import Dense

x = data[['age', 'performance']]
y = data['y']
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3, random_state = 2024)

model = Sequential()

model.add(Dense(20, input_dim = 2, activation = 'relu'))
model.add(Dense(15, activation = 'relu'))
model.add(Dense(1, activation = 'sigmoid'))
model.compile(loss = 'binary_crossentropy', optimizer = 'adam', metrics = ['accuracy'])

model.fit(x_train, y_train, epochs = 100, batch_size = 10) # fit ANN

accuracy = model.evaluate(x_test, y_test)
print(round(accuracy[1] * 100, 2))

---
Epoch 1/100
2024-06-30 22:31:06.692852: W tensorflow/core/platform/profile_utils/cpu_utils.cc:128] Failed to get CPU frequency: 0 Hz
2024-06-30 22:31:06.891137: I tensorflow/core/grappler/optimizers/custom_graph_optimizer_registry.cc:113] Plugin optimizer for device_type GPU is enabled.
140/140 [==============================] - 3s 4ms/step - loss: 0.5638 - accuracy: 0.7393
...
Epoch 100/100
140/140 [==============================] - 1s 6ms/step - loss: 0.0943 - accuracy: 0.9543
Output is truncated. View as a scrollable element or open in a text editor. Adjust cell output settings...
2024-06-30 22:32:14.638250: I tensorflow/core/grappler/optimizers/custom_graph_optimizer_registry.cc:113] Plugin optimizer for device_type GPU is enabled.
19/19 [==============================] - 1s 10ms/step - loss: 0.0848 - accuracy: 0.9617
96.17

通过查看图 4 中的 NN 决策边界，我们可以看出为什么它被认为是一种非线性分类算法。即使我们只给出了模型年龄和性能，它仍然能够构建非线性决策边界。因此，在一定程度上，模型已经为我们完成了艰苦的工作。你可以说模型的隐藏层已经自动完成了特征工程。那么，考虑到这个模型具有很高的准确性并且需要我们付出的努力较少，我们为什么还要考虑逻辑回归呢？

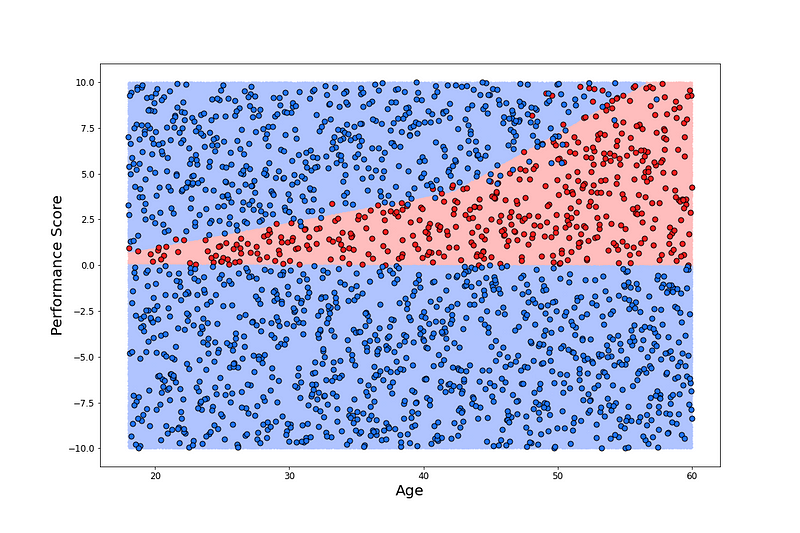
图4：神经网络的决策边界

NN 的缺点是它只能解释。这意味着，与逻辑回归不同，我们不能直接查看模型的参数来了解其工作原理7。我们可以使用其他方法，但最终，理解 NN 的工作原理更加困难。向非技术人员（例如人力资源主管）解释这一点更加困难。这使得逻辑回归模型在行业环境中更有价值。

工业界和学术界都存在许多问题，其中大多数问题都比本文给出的示例更复杂。本文提出的方法显然不是解决所有这些问题的最佳方法。例如，如果你尝试进行图像识别，那么使用逻辑回归将无济于事。对于较简单的问题，逻辑回归和对数据的良好理解通常就是你所需要的。

参考

  1. 茶桁的公共文章项目库（2024 年），https://github.com/hivandu/public_articles↩︎

  2. T. Hastie, R. Tibshirani, J. Friedman, The Elements of Statistical Learning [pg 150] (2017), https://web.stanford.edu/~hastie/ElemStatLearn/↩︎

  3. Statinfer, The Non-Linear Decision Boundary (2017), https://statinfer.com/203-6-5-the-non-linear-decision-boundary/↩︎

  4. T. Hastie, R. Tibshirani, J. Friedman, The Elements of Statistical Learning [pg 150] (2017), https://web.stanford.edu/~hastie/ElemStatLearn/↩︎

  5. R. Gall, Machine Learning Explainability vs Interpretability: Two concepts that could help restore trust in AI (2018), https://www.kdnuggets.com/2018/12/machine-learning-explainability-interpretability-ai.html↩︎

  6. UCLA, How do I Interpret Odds Ratios in Logistic Regression? (2020), https://stats.idre.ucla.edu/stata/faq/how-do-i-interpret-odds-ratios-in-logistic-regression/↩︎

  7. R. Gall, Machine Learning Explainability vs Interpretability: Two concepts that could help restore trust in AI (2018), https://www.kdnuggets.com/2018/12/machine-learning-explainability-interpretability-ai.html↩︎

特征工程的力量

https://hivan.me/特征工程的力量/

作者

Hivan Du

发布于

2024-07-01

更新于

2024-07-16

许可协议

#

喜欢这篇文章？打赏一下作者吧

评论

关注我

链接

分类

最新文章

×