对客观世界的建模：卷积

本节课为「计算机视觉 CV 核心知识」第 15 节；

「AI秘籍」系列课程：

• 人工智能应用数学基础
• 人工智能Python基础
• 人工智能基础核心知识
• 人工智能BI核心知识
• 人工智能CV核心知识
• AI 进阶：企业项目实战

可直接在橱窗里购买，或者到文末领取优惠后购买：

Hi, 大家好。我是茶桁。

我们这就要去看 LeNet，去讨论 LeNet 这个问题，讨论 CNN 统一了提特征与决策，顺便把 LeNet 给引出来。

这部分内容比较有意思，所以咱们再分几个小节来讲，分别是：

1. 对客观世界的建模：卷积
2. 从 MLP 到 CNN
3. 如何加速 CNN
4. CNN：统一了提特征和决策

第一个，是对客观世界的建模：卷积。就是要把卷积的意义稍微讨论一下。

比如第一节课讲滤波的时候，说滤波就是卷积，因为它的计算过程是一样的。

那么它为什么又叫卷积又叫滤波呢？卷积为什么能够滤波、哪里有波需要过滤掉？

要把这个事情考虑清楚，这个事情讨论清楚之后，就可以讨论从什么到 CNN 了。就是 CNN 是如何出来的。

为什么要用 CNN，举一个 MLP 的例子。MLP 是一个多层感知机

Multi layer perception。

多重感应是机器学习或者传统机器学习的一个方法。如何从它到 CNN 的。然后借助这个例子，把 CNN 统一了提特征和决策两个步骤给它讲一下。

这个讲完之后，LeNet 就引出来了，引出来之后咱们就可以讨论 LeNet 如何加速 CNN。然后后面就是总结一下就行了。

好，咱们先讨论一下卷积。原来讲图像滤波的时候用的是 cv2.filter，就是对图像进行滤波。那么图像滤波我们发现，并没有说滤掉什么波，没有说直接去操作什么波，而直接是用了一个卷积的操作。对应位置点积，再相加点积，或者叫卷积的操作。

所以，就不免要想一个问题：为什么卷积操作就能够滤波呢？滤的什么波呢？

实际上卷积的计算过程，我们来看下图：

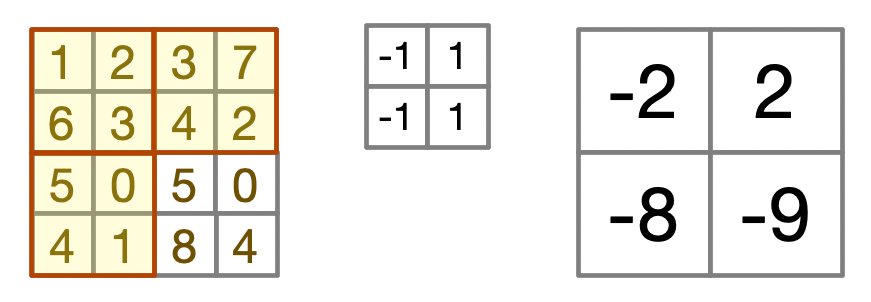
中间小的那个矩阵是一个 kernel，对图片进行卷积的操作，就是做滤波的操作。

这个 Kernel 先放在左上角第一个红色框的位置，对应位置这个像素做点积。

\[ \begin{align*} & -1 \cdot 1 + 1 \cdot 2 + 6 \cdot (-1) + 3 \cdot 1 \\ = & -1 + 2 - 6 + 3 \\ = & -2 \end{align*} \]

然后再以此移动窗口计算，那么我们就可以得到：

$$ \[\begin{align*} & -1 \cdot 3 + 1 \cdot 7 + (-1) \cdot 4 + 1 \cdot 2 \\ = & -3 + 7 - 4 + 2 \\ = & 2 \\ & \\ & -1 \cdot 5 + 1 \cdot 0 + (-1) \cdot 4 + 1 \cdot 1 \\ = & -5 + 0 - 4 + 1 \\ = & -8 \\ & \\ & -1 \cdot 5 + 1 \cdot 0 + (-1) \cdot 8 + 1 \cdot 4 \\ = & -5 + 0 - 8 + 4 \\ = & -9 \end{align*}\] $$

对应位置的像素点积，得到相应的结果，这就是卷积。

然后咱们拿到相应的结果之后，就组成了一个新的矩阵 [[-2, 2], [-8, -9]]。

卷积基本的计算过程大概就是这么一个操作，当然后面有卷积层的操作。卷积这个概念是这么操作，卷积层不是这样。卷积层呢，比如说这有个 4*4 的矩阵，可能需要 3 乘以 4*4 的图片做卷积，得到一个 6 乘以 2*2 的 feature map。这中间做卷积具体的过程怎么样呢？等一下会去讨论。现在大概知道，卷积就这么一个过程。

当前看到的卷积过程是二维的，我就 4*4 的矩阵经过 2*2 的核做卷积之后得到一个 2*2 的矩阵。其实卷积的计算过程如果把它细化一下，放到一维来看。

[1, 2, 3, 2, 1] 是一个向量， [-1, 1] 这是一个核。把核拉进去做卷积，那我们得到的结果就应该是 [1, 1, -1, -1]。这个计算过程实际上就是向量里的数字后项减前项，就得到了这么一个结果。

这是一维的卷积。因为一维的卷积比较好理解一些，二维其实有些时候不容易讲，所以用一维的去讲，去理解卷积的意义。

我们可以看到，一维这个向量经过这样的核卷积之后得到一个 [1, 1, -1, -1] 这样一个向量。 我们称这个向量是滤波。滤波这个词的意思是过滤掉某些波的意思。那么由这个上一个向量变成后一个向量何来波呢？

要滤波，首先得有波让过滤。我们先来看一小段视频：

「正弦波画曲线视频」

看这个视频，我从头给大家解说一下。这个是说给我一组正弦波，我可以表示任意曲线。

我之前那个向量是不是可以表示成曲线？[1, 2, 3, 2, 1]，实际上就是下面这样一个曲线：

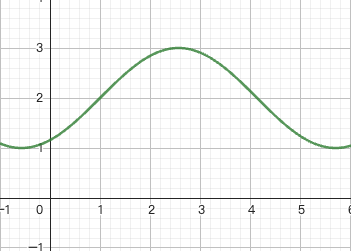
其实任意一个曲线，把这个曲线取一个计算值就是向量了。所以，在上面这个视频中，那一段话就可以改一下，改成「给我一组正弦波，我可以画出任意向量」。

看这个图

可以看到，这是产生一个正弦曲线的方法。画正弦曲线，其实可以让一个点绕一个圆周去运动，绕单位圆的圆周去运动。然后把这个点的纵坐标记录下来，随着时间的推移，把它记录下来。然后它就是一个正弦曲线了。

x 轴是一个时间，y 轴是上是坐标，纵轴的坐标就是个正弦曲线。这样的话就等于说画正弦曲线了。

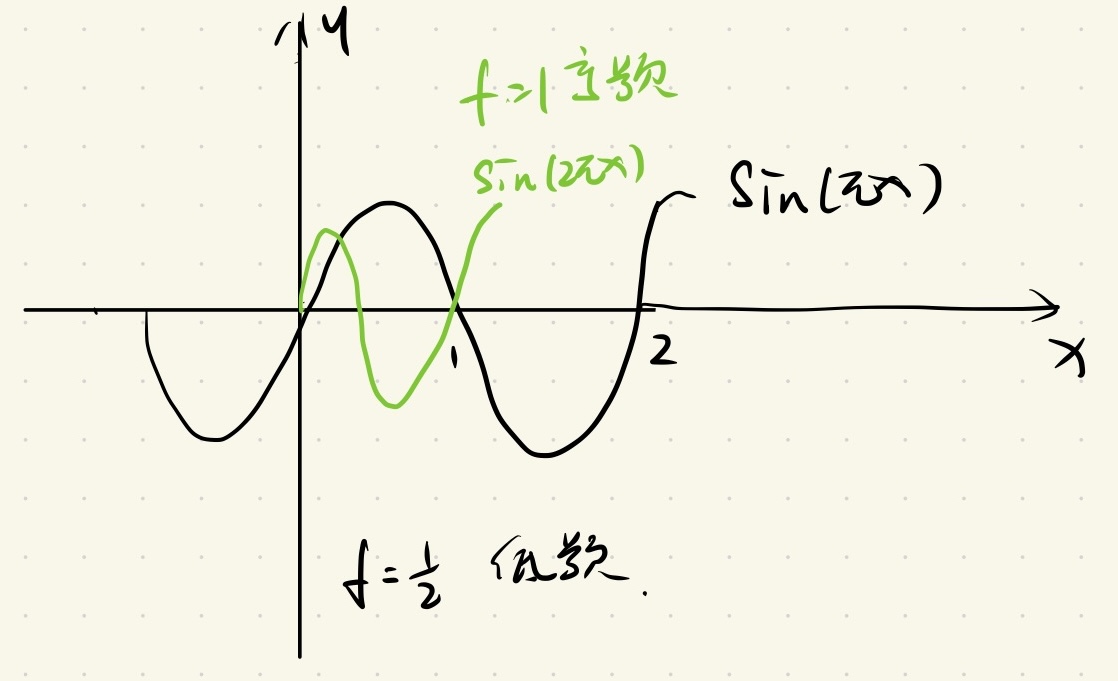
然后再看这个图

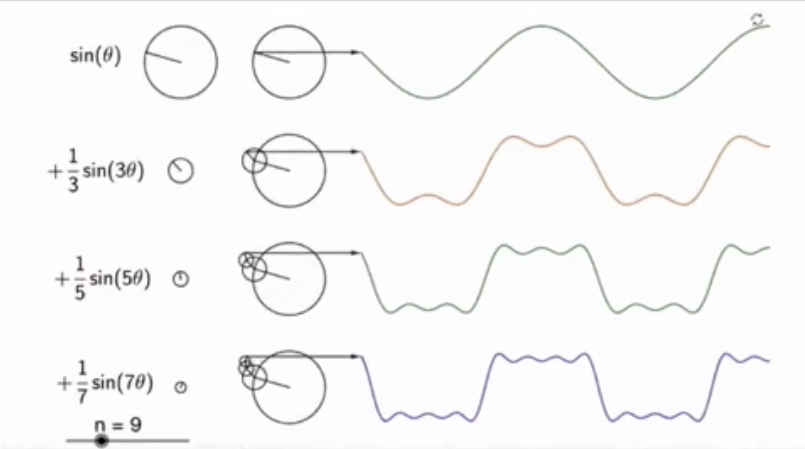
这个图中，第一个曲线就是一个正弦。那么第二段曲线呢，是一个 \(+\frac{1}{3}sin(3\theta)\)，我们可以看到这个图里有一个小圆。因为它的半径也小了，就是它的幅值。这里 1/3 是乘在 sin 前面的，它的幅值也小了，频率也高了，周期也小了。

那么这两个曲线的叠加，这样一个正弦曲线如何表示出来呢？两个圆叠加就行了。在大圆上再有个小圆就行了。

然后同样的，再加上 \(+\frac{1}{5}sin(5\theta)\)，再加上 \(+\frac{1}{7}sin(7\theta)\)，也同样的，圆叠加起来就行了。

那么这样叠加起来的效果，我们可以看到，随着叠加的进行，发现这个波形越来越像一个方波了。所谓的方波是什么波？方波就是这样的一个波：[0, 1, 0, 1, 0, 1, ....]。这个波是一种非正弦曲线的波形，通常会与电子和讯号处理时出现。理想方波只有“高”和“低”这两个值。

那么既然一堆曲线可以表示成方波，就是一组正弦波可以表示方波了。一组正弦波其实调调它的幅值、周期或者频率，调调它的相位，一组正弦波可以组成任意形状的曲线，也就是任意的向量。

接着往后看

这个例子中的图就有点像心电图了。这一组正弦波可能有 11 个正弦，你看图中，n = 11。

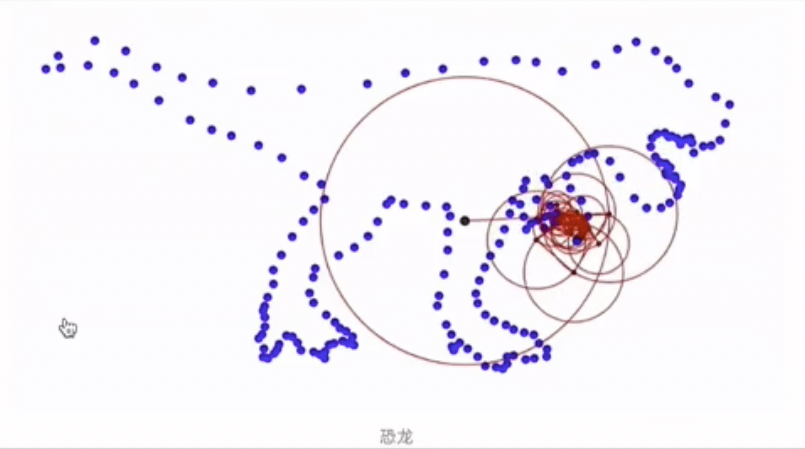
上面这张图跟前面的图不一样，这个图是点在圆周运动的时候，记录了它的 y 坐标的值，又记录了 x 坐标值。也就是说现在是一个二维的情况，不再是一维的情况了。最后是画出了一个恐龙出来。

那下面那个动画也是一样，记录了二维的情况，画出了一只猫：

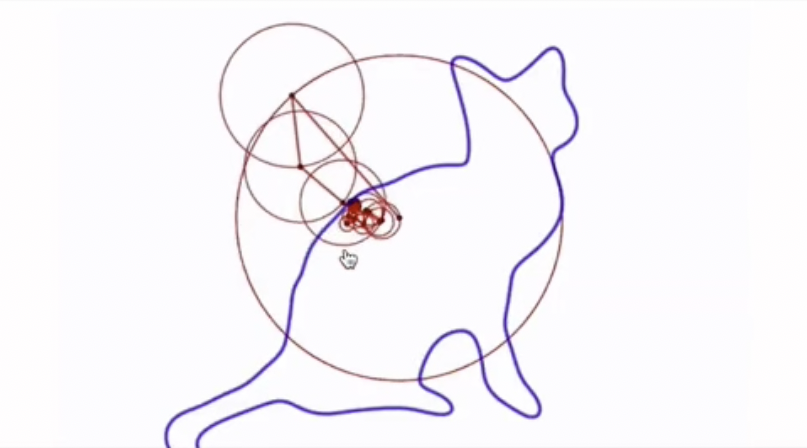
那么通过看这个视频动画大概了解一下，向量里面是含有波的。包含一种什么样的波呢？含有一种正弦波。

所以说滤波操作中的波呢就是正弦波。任意向量其实都可以表示成一组正弦波构成的。

这样，滤波就可以解释清楚了。如何去解释这个呢？原来是 [1, 2, 3, 2, 1]，现在变成了 [1, 1, -1, -1]。向量改变了，那它组成的波也改变了。组成的波改变了就可以认为是滤波了。就是改变了一些向量中波的组成。

那么后面其实要想，向量中的波到底由哪些波构成的，我们能不能把这些波给找出来，是可以的。后面就看一下怎么去找这些波。

正弦曲线的定义，我们可以用下面的式子:

\[ y = Asin(w(x+b)) \]

这个 A 就是幅值，w 就是相当于周期，或者是频率因子。这个 b 就相当于相位了，就是 sin 函数是从 0 或者从某一点开始。

所以，不同的A、w、b 的若干条正弦曲线可以叠加组成任意曲线，可以叠加组成任意向量。那么把这个曲线的公式给找出来之后，是不是有可能把这个项中所含有的那些曲线给找出来？那实际上是可以的。

看一下这个图:

我们先看的向量，或者原始的波是这最左边的那个波。这就是方波了。看到组成这个方波的正弦曲线有这条蓝色的由后面这些条波。反正很多条之后，这个曲线就有点像[-1, 1, 1, -1] 了。或者说如果说这个曲线足够小的话，人看起来是觉得它就是一条直线，它并没有波动，就是这么一个近似情况。

那么总之，图上是能够看到，同时是能够看到它是由九条波叠加而成的，也就是说刚才九个圆运动起来就可以形成这么一个方波了。

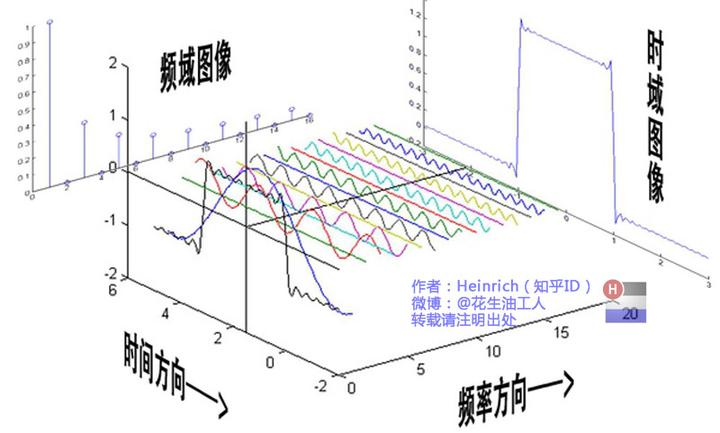
那么形成这样的方波之后，刚才说了想把这个 9 条曲线找出来，现在有人就画出图片来了。我们看这个图片显然不是人手画的，它肯定是某个软件画的。肯定是某个人操作的话，它是如何去把这个波找出来的？它必须先找出来才能画出来。

那么看一下，频率方向上表示的是频域图像，这就频域的向量。那么这个频域的向量 这在这里是什么意思？咱们注意到，在图像频率方向上左边的影射轴上，有一条最长的直线垂直于频率方向，这根直线对应的就是最前方那条蓝色的曲线，就是周期最大，频率最低的那条曲线。我们将其描成红色：

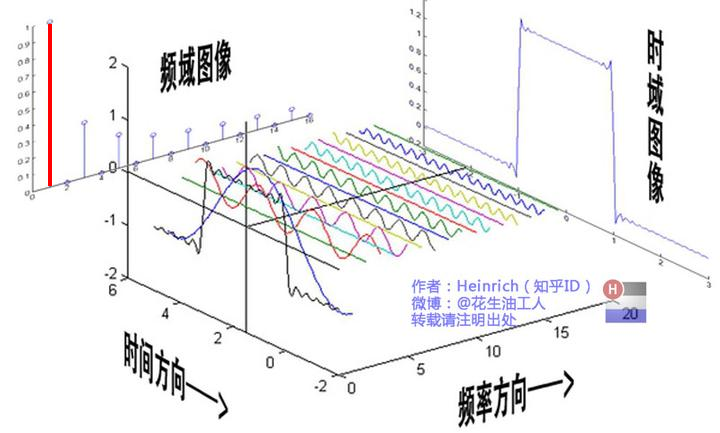
往后第二条直线对应的就是频率第 2 低的曲线,然后第三条就对着频率第 3 低的曲线。。。所以我们可以看到，这就是频域向量。这个频率方向的轴，就是指的是正弦波的频率。这些波上下震动的纵轴则是这个正弦波的幅值，也就是 A。

也就是说这两个值，各个曲线的 A 值和 w 相关的这个频率的值应该是 \(f(\frac{2\pi}{w})\)

就 A 和 f 构成的横轴向量，我们称为是频域的向量。那频域的向量就分别是 \([f_0, f_1, ..., f_8]\)，一共是 9 个。那频域的这个向量是如何得到的呢？

因为知道频域的向量，就可以知道具体的正弦波是怎样的，就可以画出这个曲线。所以刚才的问题是一个方波是由怎样的一组正弦波构成的这个问题，就转化为它对应的频率向量是什么。

那么这个频率向量是如何求呢？比如说还是这个方波，向量是 [-1, 1, 1, -1]， 我们将其定义为 v, 然后对 v 做 FFT，就得到 F:

\[ F = FFT(v) \\ F = [f_0, f_1, f_2, ..., f_8] \]

所以这里是有一个傅立叶变换，通过傅立叶变换就可以得到频域向量。那么频域向量含的这些值每一个值就代表一条正弦曲线。所以说到这里是通过看图，直观的感受到向量里边任意曲线其实可以用正弦波曲线组成，包含有波。对向量进行一个操作就相当于对波进行改变了。

那么进行改变如何控制？因为有些时候我想让这些波里频率比较低的波消失，只剩下频率比较高的波。其实想要控制，就需要先对向量进行傅立叶变换，把各种波给找到，找到之后对 F 做点积。

\[ F \cdot [0, 0, 0, 0, 1, 1, 1, 1] \]

点积呢，如果低频对应的 4 个值乘以 0，高频对应的 4 个值乘以 1，这样的话这个频率就只有高频的一些正弦波了，低频正弦波没有了。 然后我对这样的结果进行 IFFT，反傅立叶变换，又得到一个向量 v'。这时候这个 v' 相对于 v 来说就是把低频的一些正弦波给滤掉了啊，剩下一些高频的波。

从这个角度来看，要完成对 v 的滤波，我要定向的滤波或者说要有目的的滤波的话，要先对 v 进行 FFT，然后再设计一个滤波的向量，我们假设是 H，第三步再反傅立叶变换，这样才是滤波。

那为什么一个单纯的卷积就是滤波了呢？那实际上是因为还有这么一个公式：

\[ IFFT(F(x) \cdot H(x)) = f(x) * h(x) \]

如果有 f(x), 这个 f(x) 可以理解为向量，它表示一个曲线。曲线离散化以后就是一个向量了。

我们对 f(x) 进行傅立叶变换： \(F(X) = FFT(f(x))\)。然后我们对 h(x) 进行傅立叶变换： \(H(x) = FFT(h(x))\)，这个成立的话，那么上式也成立。

也就是说，在对它们进行傅立叶变换之后再点积 \(F(X) \cdot H(X)\)，然后再反傅立叶变换 \(IFFT(g(x))\)，就等于 \(f(x) * h(x)\)。 这个星号 (*) 是卷积的意思。

这个公式就是我们傅立叶变换的内容。

也就是说，两个向量 f(x)、h(x)，这两个向量傅立叶变换，结果进行点积，点积后的结果再进行反傅立叶变换，结果就等于这两个向量的卷积。

\[ \begin{align*} & F(x) = FFT(f(x)) \\ & H(x) = FFT(h(x)) \\ & IFFT(F(x) \cdot H(x)) = f(x) * h(x) \end{align*} \]

所以，我们要对 f(x) 进行滤波的话，实际上只要有一个 h(x) 就行了。我们之前设计的 H(x) 是 [0, 0, 0, 0, 1, 1, 1, 1]，它的反傅立叶变换是 h(x) 就行了。

那这样的方式就方便计算了，毕竟傅立叶变换和反傅立叶变换变来变去的计算量要高一些。

好，我们再整体梳理一下方便理解。

首先，我们得到了一组向量，之前我们假设那个方波为 [-1, 1, 1, -1]，定义为 v。

接着，我们对这组向量进行傅立叶变化: F = FFT(v)，得到的结果为 F。那这个 F 中就有各个波的值: \(F = [A_0, A_1, ..., A_8]\)。

这个时候我们需要过滤掉某些波，那我们需要设计一个 H 和得到的 F 进行点积。比如说我们想要过滤掉 \(A_0\)， 那我们就需要设计 H 为 [0, 1, 1, 1, 1, 1, 1, 1]，要滤掉的那个波在点积的时候需要 H 内的值为 0。

点积完之后这个波是什么样子，要对点积的结果进行一个反傅立叶变换，于是就有了 \(IFFT(F \cdot H)\)，得到的结果就为 v'。

这就相当于对 v 进行了一个高通滤波。因为高频率的波通过，低频率的波不通过，最后得到 v'。这个滤波的过程，先进行傅立叶变换。这是第一步，得到它有哪些波。然后第二步点积一个 h，对波进行高通化。当然这个点积除了 [0, 1] 以外也可以是 0.5, 0.8 等，有些波让其低一些，有些让其高一些。这是第二步。 然后第三步是频率对它进行转变，然后再通过反傅立叶变换再变换回来。所以反傅立叶变换就是把这些频率组成的波合成向量就行了。

这种要通过 1、2、3 步比较麻烦，实际上 v 卷积一个向量就行了：v * h。这个 h 是实际上就是 IFFT(H)。

那现在去看一个例子，来看看卷积具体的算法是什么。

小明生病吃药，刚吃，体内药物含量为 1，一天后，药物含量为 0.8，两后为 0.6，三天后 0.2. 问，小明连吃 4 天药时，体内药物含量是怎样的？

我们一般买药的时候，有的药在说明书上会有一个「体内半衰期」，半衰期是什么意思？就是在多少个小时候，体内的药物含量变成0.5。药物会在体内消耗，所以假设一天后，小明体内的药物含量就是0.8了...药物含量在体内衰减的过程如题，问小明连吃 4 天药时体内药物含量是怎样的。

那咱们就算一下这个过程，第 1 天开始，药物含量是 1，一天后是 0.8，那加上今天吃的药，第 2 天含量应该就是 1.8。第三天，也就是两条后衰减成 0.6 了，前一天吃的衰减为 0.8, 再加上今天吃的，那就是 0.6 + 0.8 + 1 = 2.4，三天后，也就是第四天，也是如前计算方法，就应该是 1 + 0.8 + 0.6 + 0.2 = 2.6，4 天后，即第 5 天，这一天已经不再吃药了，那这一天的药物含量应该是 0.8 + 0.6 + 0.2 + 0.0 = 1.6，整个过程应该如下:

\[ \begin{align*} & 1. 第 1 天: 1 \\ & 2. 第 2 天: 1 + 0.8 = 1.8 \\ & 3. 第 3 天: 1 + 0.8 + 0.6 = 2.4 \\ & 4. 第 4 天: 1 + 0.8 + 0.6 + 0.2 = 2.6 \\ & 5. 第 5 天: 0.8 + 0.6 + 0.2 = 1.6 \end{align*} \]

咱们来看，一个药物经过小明身体之后的含量变化，咱们就可以看成是一个向量。吃了 4 天药，最初的一个基础含量应该是 [1, 1, 1, 1]，经过小明的身体滤波之后变成 [1,1.8,2.4,2.6,1.6,0.8] 。我们来看这个过程，如果把它表示成公式该怎么去表示呢？

首先，咱们吃药这个过程向量表示成 x: [1, 1, 1, 1, 0, 0, 0, 0]，然后我们有一个人体的系统，药物经过人体系统代谢等功能后会发生变化，变化为 g(t) [1, 0.8, 0.6, 0.2]，我们假设这个人体系统为 g(t)。

然后 x 经过人体系统之后它会有一个过程，每天吃药每天衰减之后它是 y(t) [1,1.8,2.4,2.6,1.6,0.8,0.2,0]，就是算这个过程。

那现在要写公式，就先把这几个值具体写出来，然后看看是怎样的公式。

\[ \begin{align*} y(t) & = \sum_{i=0}^t x(i)g(t-i) \\ y(0) & = x(0) \cdot g(0) = 1 \cdot 1 = 1 \\ \\ y(1) & = x(0) \cdot g(1) + x(1) \cdot g(0) \\ & = 1 \cdot 0.8 + 1 \cdot 1 = 1.8 \\ y(2) & = x(0) \cdot g(2) + x(1) \cdot g(1) + x(2) \cdot g(0) \\ & = 1 \cdot 0.6 + 1 \cdot 0.8 + 1 \cdot 1 = 2.4 \\ y(3) & = x(0) \cdot g(3) + x(1) \cdot g(2) + x(2) \cdot g(3) + x(3) \cdot g(0) \\ & = 1 \cdot 0.2 + 1 \cdot 0.6 + 1 \cdot 0.8 + 1 \cdot 1 = 2.6 \\ y(4) & = x(0) \cdot g(4) + x(1) \cdot g(3) + x(2) \cdot g(2) + x(3) \cdot g(1) + x(4) \cdot g(0) \\ & = 1 \cdot 0 + 1 \cdot 0.2 + 1 \cdot 0.6 + 1 \cdot 0.8 + 0 \cdot 1 = 1.6 \end{align*} \]

我们来看 y(3)，用到了 x0，x1，x2，x3, 用到是 g0, g1, g2, g3。因为是 x(i)g(t-i)， 所以这里等于是把 g0, g1, g2, g3 翻转一下变成 g3, g2, g1, g0，然后对应位置相乘。这个操作就叫卷积了，上面的公式就是卷积的公式。每一个值都是由卷积得到的。

我们起始也可以用程序来实现这个操作，有些小伙伴比较容易理解程序：

import numpy as np
# 药物衰减序列
g = np.array([1, 0.8, 0.6, 0.2, 0., 0., 0., 0.])
# 服药序列
x = np.array([1, 1, 1, 1, 0, 0, 0, 0])
# 卷积操作
y = np.convolve(x, g)
# 只取前五天的结果，最后一天为继续验证
y = y[:5]
y

---
array([1. , 1.8, 2.4, 2.6, 1.6])

其实就得到这样一个概念，x 是个原始的向量，原始的向量经过人体系统之后，人体系统包含一个向量，它们两个卷积之后就得到一个新的向量。这就是卷积。

这个卷积操作就实现了一个滤波操作。滤了什么波呢？实际上就是对 g(t) 进行FFT: FFT(g(t))，得到一个 G。其内部这些值 [w0, w1, w2, ...] 是怎样的权重，它就对 x 做了怎样的滤波。

我们可以看到卷积内部都是点积，只不过是把滤波向量翻转了一下，然后再点积。那么通过这个例子能看到，卷积的计算过程实际上是由大量的点积构成，只不过是翻转了一下。

那具体自己去设计卷积核的时候，相当于在设计翻转后的卷积核。

通过这个例子，就能看到，药物含量经过人体是一个滤波的过程，相当于卷积。其实上它是对现实世界中的一种模拟。它可以模拟药物含量在人体这个系统中的消耗过程，也可以模拟光线通过玻璃之后的一些变化。

比如说咱们前几节课中那个老照片中人脸上的斑点。老照片上的人脸基本都特别光滑，没有多少斑点对吧？就是通过镜头做了一些光滑滤波.后面咱们有设计一个卷积核，尝试对人脸上的一些斑点进行滤波，斑点进行滤波的原理就在这里。实际上是把图像上的人脸设计的卷积核相当于原来那个相机镜头了。

不同的卷机核对应不同的镜头。现在已有的所有的相机的镜头都可以找到它对应的卷积核，或者叫滤波核。因为它本身这种镜头就是滤波效果。

数字卷积核是无限的，可以想表示怎么样就表示怎么样，我们实际生产出来镜头是有限的。所以说卷积相当于我们生产不出来镜头。想达到那个效果，我们就用数字滤波这种形式来达到。

所以说我们这个滤波操作或者是卷积操作能够模拟现实生活之后，它就可以做我们现实生活中做不到的一些事情，做一些扩展。从这里我们能看到，滤波这个过程既能模拟光线穿过玻璃之后成像的过程，又能模拟穿完玻璃之后玻璃对光线成像的影响，又能模拟药物在人体体内含量。其实还能模拟电子器件中电路板上的滤波效果。

我们总结一下。信号经过现实系统影响这个过程可用卷积计算来模拟表示，可以用滤波模拟表示。镜片对图像的滤波效果，比如说单反镜头也可以，收音机对电磁波的滤波也可以。

比如说，小明吃药，是对一件一段时间内的信号的处理，是一维的信号的处理。图像滤波是对一个空间信号的处理，是二维的信号的处理角度。

那么二维信号处理的角度上面那个视频后面有一个画恐龙和猫，它是二维的。那二维的波我没有显示，二维的波应该是一个石头扔在水面上荡起的那个波纹。

到这里我们就讲完了对客观世界的建模，卷积。

卷积除了我上面举的吃药的例子，它应用会非常的广。卷积应用的非常广，就是因为傅立叶变换的存在。

我们下节课继续，拜拜。