20. BI - 一篇文章为你讲透 SVD 矩阵分解的原理
本文为 「茶桁的 AI 秘籍 - BI 篇 第 20 篇」

[TOC]
Hi, 你好。我是茶桁。
之前咱们花了大概 5 节课的时间学习了推荐系统中的矩阵分解,ALS 算法以及 SlopeOne 等等。这些内容都属于协同过滤的内容,除了协同过滤之外,推荐系统还有另外一种方法,就是基于内容推荐。不过首先,咱们还是得把协同过滤讲完,当然依然还是矩阵分解,不过今天我们要讲的是 SVD 矩阵分解。
想想,咱们之前课程中所讲的矩阵分解的内容是什么?
咱们讲解了,将一个大矩阵拆成两个小矩阵,然后用一种优化方式固定一个求解另一个,就是交替最小二乘,英文应该叫做 ALS。
那今天讲的矩阵分解其实跟 ALS 相比,最后也是一样的解法,一会咱们可以一起来看一下。这个方式也是关于协同过滤的,基于内容的推荐系统将会是之后几节课中要去学习的内容。
这些都是推荐系统里面很重要的一个基石,之后我也是会带着大家一起来做一些项目,通过一些工具来去实战推荐系统的内容。
此外,我们还要考量。因为推荐系统是一个非常工程化的东西,在工程上面需要考虑的问题就会很多,比如说泛化能力。因为工程中可能会有更多的特征,希望预测的更准,就需要有更多的特征要入到模型里面去,我们之前的矩阵分解考虑的特征维度可能并没有那么多,所以工程上面还会有更泛化的一种模型,这是一种考量的维度。
还有一个考量维度就是我们的计算设备,现在我们进行计算都是在本地计算机来进行计算的,当数据量比较大的时候你电脑的内存和 CPU 都会被占满,你就无法去进行其他的工作。所以我们今天也看一看如何去使用一些云端的在线编程的工具来去加速你的运算,尤其是当你遇到一些需要 GPU 的环境的时候可以使用它来进行提速。
这两个都可以说是工程上面重要的内容。一个设备,一个是泛化能力,使用更多的一些特征,让模型的计算会更加的准确。
那我们对将要讲解的内容做一个分解,首先会先讲一下 SVD 矩阵分解,然后会在更之后的课程中开始给大家讲到基于内容的推荐。咱们先来看看 SVD 的矩阵分解,看一看矩阵分解背后的原理,看看普通矩阵的矩阵分解,对称矩阵的矩阵分解。
咱们知道 SVD 的中文叫做什么?就是前面跟大家说的,这个叫做奇异值分解,它的一个主要的领域是做降维的处理,把很多的维度抽出来几个主要特征。降维是一种思想,可以用到很多场景里面。后面的课程中也会给大家看一看一个图像的降维是如何来通过 SVD 来进行压缩的,在推荐系统里面 SVD 又是怎样起到作用的?
我们在工具上面使用会用到 SVD 算法家族,包括 FunkSVD,BiasSVD,SVD++,这 3 个方法是在我们之前的课程中给大家介绍的一个工具家族里面,它应该也是关于 scikit 这个家族,scikit 最常见的是它的机器学习的工具 scikit-learn,也称之为 sklearn。
之前的课程中,给大家使用的一个推荐系统的工具箱,就是 scikit 家族的,就是 surprise。不知道有多少小伙伴看过之前的课程,还回忆的起来吗?
它还有一些工具今天会看到,就是我刚才提到的 SVD 算法家族。
在最开始的时候先对 SVD 有一些认知,然后我就会带着大家一起来去调包,去求解它,最后还是用我们的 MovieLens 来进行推荐。
以上的环节都是关于矩阵分解的,矩阵分解大家一定记住它是协同过滤的。还记得我们之前课程中给大家的一个树图吗?那个图中的结构要有概念。
不过咱们一节课的内容肯定是讲不完这么多,会分几节课将它们全部讲完。讲完这些之后,咱们再来看基于内容的推荐的相关内容,稍微晚一点的课程中会给大家讲到。
基于内容的推荐和协同过滤之间区别是什么?推荐系统里面两种主要的算法模型就是协同过滤和基于内容推荐,它是从数据本身的属性来去考量的。如果一个用户有了行为,我们就会把行为的数据作为一个矩阵来去做分解,就会用到协同过滤。如果这个用户没有行为,我们要用他的静态属性。
一个静态,一个动态,这些都是我们以前讲过的知识。如果大家忘记就回过头去好好看看前面的文章,把以前学过的知识做一个复习。
内容推荐系统怎么做?我们后面会带来一个酒店推荐系统的项目一起来去做一个搭建,抽取它的特征。当一个用户看了一个酒店以后即使他以前没有点击的行为,我同样可以给他做基于内容的推荐。
咱们先来回顾一下矩阵分解所处的位置:
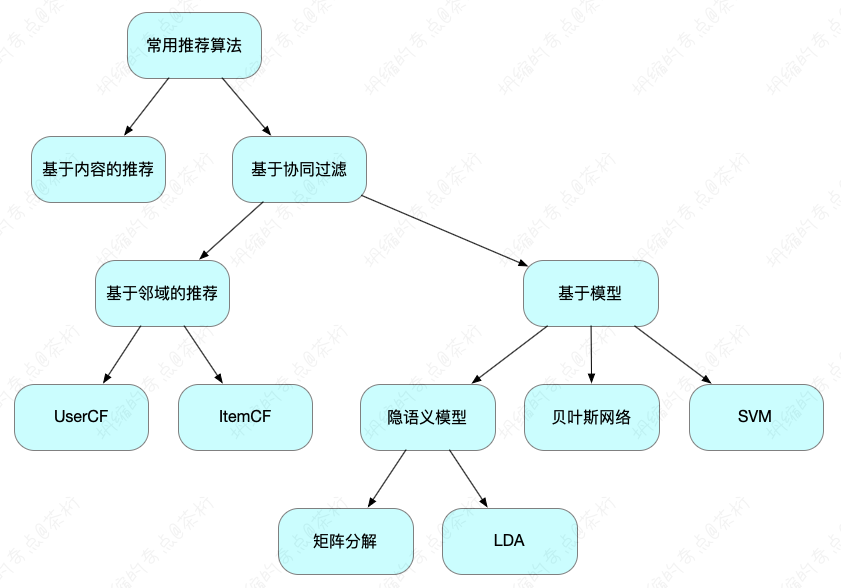
基于内容的推荐和基于协同过滤的推荐这是两种主流的方式,矩阵分解是在协同过滤里面,同样是在基于模型的这个过程。
那我们还记得之前讲过的,基于模型是什么概念?我们把它称为叫基于模型,是因为我们要去建一个模,这样我们就需要用到机器学习,所以它会分成两个阶段:训练和预测。
先拿一个数据喂给它去拟合一些参数,拟合好参数以后就可以去做预测了。矩阵分解就是这个原理,我们把原来的这些数据作为训练集,未知的去作为待预测的结果值。所以它是在基于模型里面,同时它中间是基于隐特征 latent factor。
最开始的矩阵分解实际上它并不是直接拆成两个矩阵,我们先看一看最基本的概念。
普通矩阵的矩阵分解
矩阵分解实际上是把一个大矩阵拆成多个矩阵的乘积,这是矩阵分解的概念。在矩阵分解中是有特征值的分解和奇异值的分解。
我们以前在大学期间可能学过一个线性代数的课程,这个课程里面我们会有一个矩阵,会把这个矩阵拆成特征值和特征向量的表达方法,称之为普分解。今天咱们不去推导具体的一些公式,只让大家知道有这样的一个原理。
那什么是特征值和特征向量?一个矩阵是具有一定的性质。N 维非零向量 v 是 N 乘以 N 的矩阵 A 的特征向量,而且仅当下式成立:
\[ \begin{align*} Av = \lambda v \end{align*} \]
A 就是这个矩阵,我们做一个 v,v 这里代表的是一个向量,那么拿这个向量去作用一个矩阵就相当于对这个向量做了一个拉伸的操作。lambda (\(\lambda\)) 代表的就是我们的特征值,称为标量。v 为特征值 lambda 对应的特征向量。
那咱们知道什么是标量什么是向量的概念吗?
标量是一个单独的数值,它只有大小,没有方向。在数学和物理学中,常见的标量包括时间、温度、质量等。标量通常用来描述物理量的大小。
向量是具有大小和方向的量。向量可以用来表示空间中的位置、速度、力等。它由一组有序数值组成,并且可以在空间中表示为从一个点指向另一个点的箭头。向量的常见表示方式包括列向量和行向量。
对于一个线性变换或矩阵,特征值是一个标量,表示在某个方向上的伸缩比例。特征值描述了变换或矩阵对应的特定方向上的影响程度。特征值是通过解决矩阵的特征方程来计算的。
对于一个线性变换或矩阵,特征向量是与特征值相关联的向量,表示在特征值对应的方向上的不变方向。特征向量在进行特征值分解时起着重要作用,它们描述了线性变换或矩阵在不同方向上的不变性。
特征向量是与特征值相关联的向量。特征向量描述了线性变换或矩阵在特定方向上的不变性,即在这些方向上的伸缩和旋转。特征值则表示了在对应特征向量方向上的伸缩比例。
在特征值分解中,特征向量和特征值是一对一对应的。特征向量决定了矩阵变换的方向,而特征值决定了变换在这些方向上的比例。
我们要去求解这个过程, 回忆一下,以前大概是要建一个特征的多项式。
\[ \begin{align*} |A-\lambda I|=0 \end{align*} \]
想求这样的一个解等于 0 的特征多项式, 令 \(p(\lambda):=|A-\lambda I|=0\) 称为矩阵的特征多项式。
特征多项式是关于 lambda 的 N 次多项式,特征方程有 N 个解。
\(|A-\lambda I|\) 这个值还可以再拆出来,对多项式\(p(\lambda)\)进行隐式分解,最终可以把它拆成以下的形式。
\[ \begin{align*} p(\lambda) = (\lambda - \lambda_1)^{n_1}(\lambda - \lambda_2)^{n_2}...(\lambda - \lambda_k)^{n_k} = 0 \end{align*} \]
其中
\[ \begin{align*} \sum_{i=1}^k n_i = N \end{align*} \]
拆的过程实际上是个因式分解的过程,当这一串等于 0,就可以把一个特征值\(\lambda_i\)给它求出来了。每一个特征值只要带进去都可以得到以下的一个结论
\[ \begin{align*} (A-\lambda_i I)v = 0 \end{align*} \]
这就是特征值的求法。
说起来有点抽象,我们来看一看在数学的工具里面是如何来去求解特征值和特征向量的,以一个 A 为例:
\[ \begin{align*} A = \begin{bmatrix} 4 & 2 & -5 \\ 6 & 4 & -9 \\ 5 & 3 & -7\end{bmatrix} \end{align*} \]
这是一个原始的矩阵,要想求特征值和特征向量是通过构造一个特征方程来去完成的。这个特征方程你可以用 A 减去 lambda I,也可以把它倒过来,lambda I 减去 A
\[ \begin{align*} |\lambda I - A | = \begin{bmatrix} \lambda - 4 & -2 & 5 \\ -6 & \lambda - 4 & 9 \\ -5 & -3 & \lambda + 7\end{bmatrix} = 0 \end{align*} \]
这里的 I 应该就是一个单位的对角阵,对角阵大概就是对角线为 1,其他地方为 0。
\[ \begin{align*} p(\lambda):=|\lambda I - A| = \lambda ^2 \cdot (\lambda -1) \end{align*} \]
所以 lambda I 减去 A 等于 0,它通过一些行列式的组合可以得出来。
\[ \begin{align*} & \lambda ^2 \cdot (\lambda - 1) = 0 \\ 求解得: & \lambda_1 = 1, \lambda_2 = \lambda_3 = 0 \end{align*} \]
总之,我们通过特征方程是可以求出来特征值的,然后又通过特征值代入进去也可以把特征的向量求出来。
\[ \begin{align*} & 当 \lambda_1 = 1, (\lambda_1 I - A) = \begin{bmatrix} - 3 & -2 & 5 \\ -6 & -3 & 9 \\ -5 & -3 & 8\end{bmatrix} \\ & 简化得到: \begin{bmatrix} 1 & 0 & -1 \\0 & 1 & -1 \\ 0 & 0 & 0\end{bmatrix} \\ & 所以 (E-A)x = \begin{bmatrix} 1 & 0 & -1 \\0 & 1 & -1 \\ 0 & 0 & 0\end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \\ x_3\end{bmatrix} = 0 \\ & 即: \begin{cases} x_1 - x_3 = 0 \\ x_2 - x_3 = 0 \end{cases}, 令 x_1 = 1, 得到特征矩阵 \varsigma_1 = \begin{bmatrix} 1 \\ 1 \\ 1\end{bmatrix} \\ & 同理, 当 \lambda_2 = \lambda_3 = 0, 计算可得特征矩阵 \\ & \varsigma_2 = \varsigma_3 = \begin{bmatrix} 1 \\ 3 \\ 2\end{bmatrix} \end{align*} \]
可能大家以前应该学过一门课,在大学期间有学过线性代数。那如果你没学过或者遗忘了,可以回头去看看我之前给大家写的基础数学篇,那里对人工智能所要用到的数学知识都有详细的给大家讲了一遍:《茶桁的AI秘籍 - 数学篇》。
不过我们其实不用自己去做,实际上在计算机里面有很好的解决方式,稍后给大家看一看在 NumPy 里就有一个工具,可以直接把矩阵的特征值和特征向量依次进行求解。
如果你是一个方阵,比方说 A 是 N 乘 N 维的方阵。方阵是什么概念,就是它的维度,宽和长都是相等的。对矩阵 A 进行特征分解,那么我们对它做分解就可以把它拆成这样的矩阵:
\[ \begin{align*} A = U\Lambda U^{-1} \end{align*} \]
U 的列向量是 A 的特征向量,\(U^{-1}\)是幂运算,其实计算起来还是有点难计算的。中间\(\Lambda\)是对角矩阵,元素是特征向量的特征值。
\[ \begin{align*} & A = \begin{vmatrix} 5 & 3 \\ 1 & 1 \end{vmatrix} \\ & \begin{bmatrix} 5 & 3 \\ 1 & 1 \end{bmatrix} = \begin{bmatrix} 0.97760877 & -0.54247681 \\ 0.21043072 & 0.840007078 \end{bmatrix}\begin{bmatrix} 5.64575131 & 0 \\ 0 & 0.35424869 \end{bmatrix}\begin{bmatrix} 0.97760877 & -0.54247681 \\ 0.21043072 & 0.840007078 \end{bmatrix}^{-1} \end{align*} \]
中间是它的对角阵,是一个元素的特征值。
有时候我们可以把它拆成两个部分,这是一个方阵的一个概念。
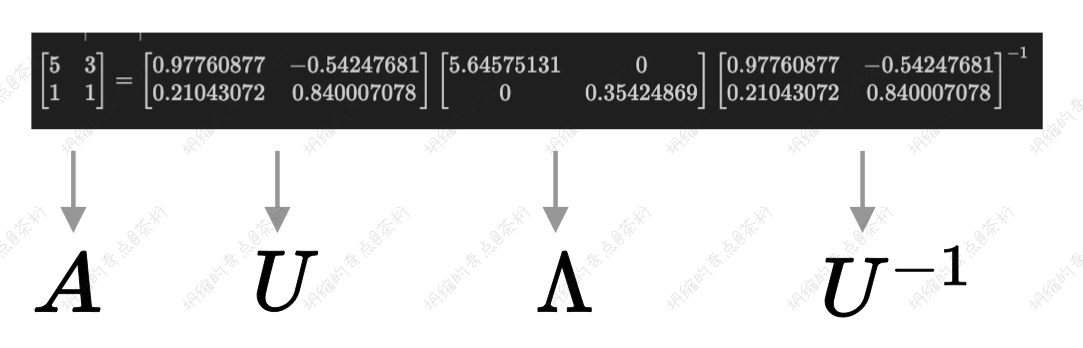
特征值 5.64575131 对应的特征向量为[0.97760877 0.21043072],特征值 0.35424869 对应的特征向量为[-0.54247681 0.840007078],特征向量之间一定线性无关。
假设我们是有线性相关,那最后这个特征向量还会存在吗?应该就不会存在了,它一定会通过一些线性的方程把它消掉。所以我们得到的这些向量都是线性无关的一个逻辑。
来看一看在计算机里面是怎么样去求解一个矩阵的特征值和特征向量的:
1 | |
刚才我们提到通过 NumPy,NumPy 是 Python
里面科学的计算工具,它里面也包含了矩阵的计算方法,我们先通过np.array创建了一个
2 乘以 2 的一个数组,然后把这个 A 进行一个分解,分解成 Lambda 和
U,Lambda 和 U 就直接可以求出来。Lambda 是它的特征值,U
是它的特征向量。那我们执行之后的结果就如打印结果一致。
对称矩阵的矩阵分解
上一节是对一个普通的方阵进行分解。如果存在一个对称方阵,对称方阵就是它不光是方阵而且它还存在对称性,上三角和下三角是对称的。
以这个方阵为例:
\[ \begin{align*} A = \begin{vmatrix} 5 & 1 \\ 1 & 1\end{vmatrix} \end{align*} \]
你看它就是个对称的,除了对角线以外两边是对称的一个结构。如果是个对称方阵就会存在一个性质,就是:
\[ \begin{align*} U^T = U^{-1} \end{align*} \]
\(U^T\) 这里的 T 代表什么概念?在写 Python 过程中我们实际上也有这样 T 的一种写法,就是把一个矩阵给它颠倒一下,倒过来,它是一个转置的概念。
如果等于它的转置,我们就可以把 A 写成以下的一个公式:
\[ \begin{align*} A = U\Lambda U^{T} \end{align*} \]
U 的列向量是 A 的特征向量,\(\Lambda\) 是对角矩阵,元素是特征向量的特征值。
\(U^T\) 这里就代表是一个转置的概念,所以具体来去看向量和向量之间,之前一定是线性无关的,最后我们还发现有个神奇的特征,不仅仅线性无关,而且还是一个正交的性质。
\[ \begin{align*} & A = \begin{vmatrix} 5 & 1 \\ 1 & 1 \end{vmatrix} \\ & \begin{bmatrix} 5 & 1 \\ 1 & 1 \end{bmatrix} = \begin{bmatrix} 0.97324899 & -0.22975292 \\ 0.22975292 & 0.97324899 \end{bmatrix}\begin{bmatrix} 5.23606798 & 0 \\ 0 & 0.76393202 \end{bmatrix}\begin{bmatrix} 0.97324899 & 0.22975292 \\ -0.22975292 & 0.97324899 \end{bmatrix}^{-1} \end{align*} \]
在这个过程中,特征值 5.23606798 对应的特征向量为[0. 97324899 0.22975292], 特征值 0.76393202 对应的特征向量为[-0.22975292 0. 97324899]
我们把两个向量去做一个乘法,最后做一个相加
\[ \begin{align*} 0.97324899 * -0.22975292 + 0.22975292 * 0.97324899 = 0 \end{align*} \]
咱们来看,他们的角度是等于多少度? 如果等于 0 这两个应该是等于多少度?我们把这两个向量做一个对位相乘,相乘以后再做一个加法最后你发现它等于零,这里应该就是 90 度。
所以这两个向量它不光是线性无关的,而且它还是个正交的向量。那代码上和之前的并没什么区别,就是矩阵换了一下,大家可以自己写一写。
我们来看矩阵的计算过程:
\[ \begin{align*} A = \lambda_1u_1u_1^T + \lambda_2u_2u_2^T \end{align*} \]
最终一个对称方阵如果它有两个 Lambda,就是两个特征值,就可以由我们的 U1 和 U1 的转置加上 U2 乘上 U2 的转置,这样我们就会把一个矩阵拆成两块,做了一个组成。就是一个矩阵等于两个部分的相加,就像上面这个式子。
lambda1 和 lambda2 拆出来的是 U1 和 U1 的转置,U2 和 U2 的转置。把它相加以后发现我们可以把一个矩阵进行还原,所以一个大的矩阵是可以拆成多个组成部分。
\[ \begin{align*} 5.23606798 * \begin{bmatrix} 0.97324899 \\ 0.22975292 \end{bmatrix}[0.97324899 0.22975292] + 0.76393202 * \begin{bmatrix} -0.22975292 \\ 0.97324899 \end{bmatrix}[-0.22975292 0.97324899] = \begin{bmatrix} 5 & 1 \\ 1 & 1 \end{bmatrix} \end{align*} \]
可以通过它来进行还原,这个性质是对称矩阵的一种性质。
奇异值分解 SVD
前面说了这么多的一些铺垫,其实想要解决的是一个普通矩阵的问题,我们要面临的问题就是,一个矩阵多数情况下是对称的吗?对于任何的矩阵来说,它很有可能不是对称的,此外它很有可能不是方阵。那前面这么好的性质怎么办?不利用就会可惜了。所以我们要构造一下。
对于任何的一个矩阵如果它的维度是 m 乘以 n,有没有可能去构造一个对称方阵。用 A 乘上 A 的转置: \(A \cdot A^T\),然后再用 A 的转置乘上 A: \(A^T \cdot A\), 我们来看,它是不是一个方阵?一起来算一下。
如果 A 的维度是 (m, n),那 A 的转置的维度等于多少咱们应该能清楚吧?转置就是把它颠倒,所以它的维度应该是(n, m),这两个矩阵如果做个乘法,乘完以后它的维度会是等于多少?
矩阵的乘法有个前提条件,就是它中间这两项一定是相等的:\((m, n) \cdot (n, m)\),那中间 n 等于 n,所以可以把 n 消掉,就变成了(m, m)。所以 A 乘上 A 的转置就变成了(m, m)的一个维度了。那它是不是方阵?很明显是方阵。
再换个角度,A 的转置乘上 A,那前面就应该是(n, m),后面是(m, n)这两个维度,那相乘之后就会变成(n, n)的维度。
所以它们两个都是一个方阵,你看这个是不是很巧妙?通过构造了两个矩阵的相乘,就得到了两个方阵。所以在计算过程中就可以巧妙的运用到以前的一个性质。
因为 \(AA^T\) 与 \(A^TA\) 是对称的方阵,我们可以将 A 和 A 的转置矩阵进行相乘,得到对称方阵:
\[ \begin{align*} AA^T = P\Lambda_1P^T \end{align*} \]
对于对称方阵我们前面刚才给大家说了一个定理,这个是存在的一个数学定理。那我们可以把 P 看成是一个 lambda, 对于前面这个 lambda 我们把它看成是 P,那么 P 乘上它的对角矩阵\(\lambda_1\),再乘上 P 的转置。
下面的式子中,我们把 lambda 看成 Q, 然后乘上\(\Lambda_2\)和 Q 的转置。 \[ \begin{align*} A^TA = Q\Lambda_2Q^T \end{align*} \] 这个是我们得出来的两个对称矩阵的性质。此时\(\Lambda_1\)和\(\Lambda_2\)是一个对角矩阵,它是应该有一个相同的非零特征值。
那这个特征值实际上是被乘过了两次,A 乘上 A 的转置,里面都有一个相同的特征值被乘上了两遍,所以是可以把它的特征值依次来进行求解。
假设这些特征值为\(\sigma_1, \sigma_2, ..., \sigma_k\), k 不超过 m 和 n, 也就是 k <= min(m, n)。此时矩阵 A 的特征值
\[ \begin{align*} \lambda_1 = \sqrt \sigma_1, \lambda_2 = \sqrt \sigma_2, ..., \lambda_k = \sqrt \sigma_k \end{align*} \]
如果前面这个矩阵它的特征值是 \(\lambda_1\) 一直到 \(\lambda_k\), 那我们就可以求到原始的 \(\lambda_1\),原始的 \(\lambda_1\) 求完以后也可以把后面的维度都给它求解出来,最终就可以让一个普通的矩阵等于三个部分的组成,我们可以得到为奇异值分解:
\[ \begin{align*} A =P\Lambda Q^T \end{align*} \]
P 我们把它称之为左奇异矩阵,它的维度是(m, m);Q 是右奇异矩阵,它的维度是(n, n)。你可以简单的去做一个还原,可以看一看对于一个 A 它是(m, n)的一个维度,如果你的 P 就是(m, m),中间这个应该是(m, n),那你把它乘一下,把中间的 m 消掉,就变成(m, n),后面 Q 是(n, n),再继续相乘,它就是等于(m, n),我做了一个示例给大家,能更直观一些:

基于刚才的一个原理,我们可以把中间的这个特征值\(\lambda_1, \lambda_2, ..., \lambda_k\)求解出来。你可以把前面的 P 和 Q 求解出来,也就是说作者想跟我们证明对于任何的一个矩阵是如何来通过一些数学工具,可以自动的把它拆成三个矩阵的相乘。而中间这个矩阵比较特殊,它是个对角线上的非零元素特征值。
特征值的概念怎么去理解,一般我们把特征值可以看成是一个权重的概念,就是在某一个特征上面它是明显的还是不明显的,如果权重越大就是比较明显的。
前面的 P 算一个特征,Q 算个特征,中间的 lambda 算是一个权重,代入到推荐系统的场景,P 这个左奇异矩阵可以称之为用户矩阵,user 矩阵,\(Q^T\) 呢,右奇异矩阵当然就是商品矩阵,item 矩阵。
以之前我们讲解的推荐系统为例,我们之前举了一个 12 个用户和 9 个电影之间的交互行为。所有的数据都是保存的用户和商品之间的打分的情况,最后抽取出来的 P 可以把它理解成为是对于用户的向量表达,而后面这个 Q 就是对于商品的向量表达。这个我们就会把它作为特征的提取,相当于是用户的特征和商品的特征,而我们中间的部分就是个权重的概念。这就是作者巧妙的把一个矩阵的分解带入到推荐系统里面,得到了它相关的一些对应的关系。
上面这些就是咱们数学的一些基础,可能说起来稍微有些抽象。看不太明白的同学可以回头去看看我为大家写的「数学篇」, 好好的学习一下。
对任何的矩阵,如果你自己去做,不用 Python,不用代码来做应该是怎样的。
比如,
\[ \begin{align*} A = \begin{bmatrix} 1 & 2 \\ 1 & 1 \\ 0 & 0 \end{bmatrix} \end{align*} \]
其实逻辑应该是用 A 乘上 \(A_T\),得到
\[ \begin{align*} AA^T & = \begin{bmatrix} 5 & 3 & 0 \\ 3 & 2 & 0 \\ 0 & 0 & 0 \end{bmatrix} \\ A^TA & = \begin{bmatrix} 2 & 3 \\ 3 & 5 \end{bmatrix} \end{align*} \]
上面一个方阵特征向量 P,
\[ P = \begin{bmatrix} 0.85065081 & -0.52573111 & 0 \\ 0.52573111 & 0.85065081 & 0 \\ 0 & 0 & 1 \end{bmatrix} \]
特征值 Lambda
\[ \sigma_1=6.85410197, \sigma_2 = 0.14589803, \sigma_3 = 0 \]
然后后面的方阵特征向量 Q 的转置:
\[ Q^T = \begin{bmatrix} -0.52573111 & -0.85065081 \\ -0.85065081 & 0.52573111 \end{bmatrix} \]
特征值
\[ \sigma_1 = 6.85410197, \sigma_2 = 0.14589803 \]
那我们就可以将中间\(\Lambda\)这个部分的特征值求解出来
\[ \lambda_1 = \sqrt \sigma_1 = 2.61803399, \\ \lambda_2 = \sqrt \sigma_2 = 0.38196601 \]
然后咱们代入进去,得出来就是这样的一个解:
\[ P\Lambda Q^T = \begin{bmatrix} 0.85065081 & -0.52573111 & 0 \\ 0.52573111 & 0.85065081 & 0 \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} -0.52573111 & -0.85065081 \\ -0.85065081 & 0.52573111 \end{bmatrix} = \begin{bmatrix} 1 & 2 \\ 1 & 1 \\ 0 & 0 \end{bmatrix} \]
那这就是我们如何去自己人工来做拆解的过程。
其实在计算机里面还是有很多工具可以帮我们去计算的。在前面得到一个性质,它最终的一个结论是这样的一个结论:
\[ \begin{align*} & 奇异值分解 \\ A & = \lambda_1p_1q_1^T + \lambda_2p_2q_2^T + ... + \lambda_kp_kq_k^T \end{align*} \]
任何的矩阵都可以有 k 个组成部分,就是把 k 个维度相加就等于一个矩阵的还原。这 k 个维度是它对角线的一个权重特征,lambda1,lambda2 一直到 lambdak,它有 k 个部分,每个部分的相乘都是等于 P1 和 Q1 的转置。
实际上 P 和 Q 这两个部分你可以把它理解成用户向量和商品向量的一个转置的乘积,前面的 Lambda 代表它的特征的大小。我们把这些值做一个累加,就等于一个原始的一个矩阵。
其实真正使用起来可以直接套用 Python 代码
1 | |
A 是一个矩阵,我们套用的方法是 SVD,SVD 就是奇异值的矩阵分解。通常我们说到矩阵分解的时候,如果去看招聘 GD,里面的一些关键词或者在网上也介绍矩阵分解,基本上都会提到一个 SVD 的概念。
那我们这就把 SVD 背后的原理简单给大家说完了,就是如何把一个矩阵拆成 3 块。SVD 它背后是个数学工具,这个工具就是拆矩阵的工具。我们现在可以知道它的作用,数学推导不是我们必修的,只是跟大家说它背后有这套逻辑,真正要使用就可以用一个 Python 的工具箱。
代入进去以后就拆成了三个矩阵,P、S 和 Q,给它任何一个矩阵都可以拆成 3 块。那大家可以自己拿代码去跑一下。咱们之前讲的时候,中间的 lambda,我这里是用 S 来做了一个替代。
运行后的结果,P 是个矩阵,Q 是个矩阵,S,也就是 lambda 是它的一个权重。它的权重已经默认帮我们从从大到小做了个排序,那就说它前面这个分量是最主要的特征,是 2.61 的权重值。
好刚才讲了这么多,那到底能产生怎样作用,或者说 SVD 怎么用,对我们有怎样的价值?矩阵其实是做运算的一个根基,那下一节课,咱们就来做一个图片压缩的例子,来更好的理解一下。
20. BI - 一篇文章为你讲透 SVD 矩阵分解的原理
