发表AI 秘籍 / 核心能力基础

23. 深度学习 - 多维向量自动求导

茶桁的 AI 秘籍 核心能力 23

Hi, 你好。我是茶桁。

前面几节课中，我们从最初的理解神经网络，到讲解函数，多层神经网络，拓朴排序以及自动求导。可以说，最难的部分已经过去了，这节课到了我们来收尾的阶段，没错，生长了这么久，终于到迎接成果的时候了。

好，让我们开始。

我们还是用上一节课的代码：21.ipynb。

我们上一节课中，实现了自动计算的部分。

1
2
3
for node in sorted_nodes[::-1]:
    print('\n{}'.format(node.name))
    node.backward()

结果我就不打印了，节省篇幅。

那我们到这一步之后，咱们就已经获得了偏导，现在要考虑的问题就是去更新它，去优化它的值。

1
2
3
4
learning_rate = 1e-5

for node in sorted_nodes:
    node.value = node.value + -1 * node.gradients[node] * learning_rate

node 的值去更新，就应该等于它本身的值加上一个 -1 乘以它的偏导在乘以一个learning_rate, 我们对这个是不是已经很熟悉了？我们从第 8 节线性回归的时候就一直在接触这个公式。

只不过在这个地方，x, y 的值也要更新吗？它们的值是不应该去更新的，那要更新的应该是 k, b 的值。

那么在这个地方该怎么办呢？其实很简单，我们添加一个判断就可以了：

1
2
3
for node in sorted_nodes:
    if node.is_trainable:
        node.value = node.value + -1 * node.gradients[node] * learning_rate

然后我们给之前定义的类上加一个变量用于判断。

1
2
3
4
5
class Node:
    def __init__(..., is_trainable=False):
        ...
        self.is_trainable = is_trainable

在这里我们默认是不可以训练的，只有少数的一些是需要训练的。

然后我们在初始化的部分把这个定义的值加上：

1
2
node_k = Placeholder(name='k', is_trainable=True)
node_b = Placeholder(name='b', is_trainable=True)

对了，我们还需要将 Placeholder 做些改变：

1
2
3
4
5
class Placeholder(Node):
    def __init__(..., is_trainable=False):
        Node.__init__(.., is_trainable=is_trainable)
        ...
    ...

这就意味着，运行 for 循环的时候只有 k 和 b 的值会更新，我们再加几句话：

1
2
3
4
5
6
7
8
9
for node in sorted_nodes:
    if node.is_trainable:
        ...
        cmp = 'large' if node.gradients[node] > 0 else 'small'
        print('{}的值{}，需要更新。'.format(node.name, cmp))

---
k 的值 small，需要更新。
b 的值 small，需要更新。

我们现在将 forward, backward 和 optimize 的三个循环封装乘三个方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def forward(graph_sorted_nodes):
    # Forward
    for node in sorted_nodes:
        node.forward()

def backward(graph_sorted_nodes):
    # Backward
    for node in sorted_nodes[::-1]:
        print('\n{}'.format(node.name))
        node.backward()

def optimize(graph_sorted_nodes, learning_rate=1e-3):
    # optimize
    for node in sorted_nodes:
        if node.is_trainable:
            node.value = node.value + -1 * node.gradients[node] * learning_rate
            cmp = 'large' if node.gradients[node] > 0 else 'small'
            print('{}的值{}，需要更新。'.format(node.name, cmp))

然后我们再来定义一个 epoch 方法，将 forward 和 backward 放进去一起执行：

1
2
3
def run_one_epoch(graph_sorted_nodes):
    forward(graph_sorted_nodes)
    backward(graph_sorted_nodes)

这样，我们完成一次完整的求值 - 求导 - 更新，就可以写成这样：

1
2
run_one_epoch(sorted_nodes)
optimize(sorted_nodes)

为了更好的观察，我们将所有的 print 都删掉，然后在 backward 方法中写一个观察 loss 的打印函数：

1
2
3
4
5
6
def backward(graph_sorted_nodes):
    # Backward
    for node in sorted_nodes[::-1]:
        if isinstance(node, Loss):
            print('loss value: {}'.format(node.value))
        node.backward()

然后我们来对刚才完整的过程做个循环：

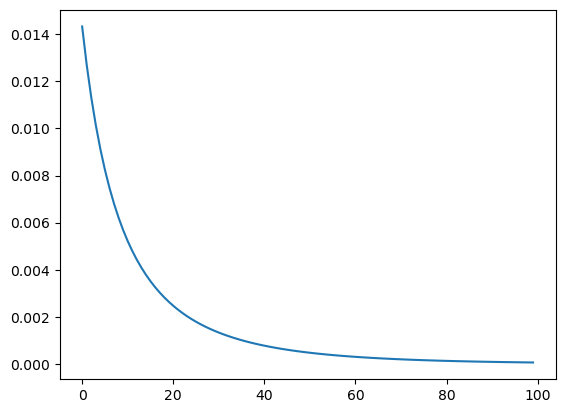
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 完整的一次求值 - 求导 - 更新：
for _ in range(10):
    run_one_epoch(sorted_nodes)
    optimize(sorted_nodes, learning_rate=1e-1)

---
loss value: 0.12023025149136042
loss value: 0.11090709486917472
loss value: 0.10118818479676453
loss value: 0.09120180962480523
loss value: 0.08111466190584131
loss value: 0.0711246044819575
loss value: 0.061446239826641165
loss value: 0.05229053883349982
loss value: 0.043842158831920566
loss value: 0.036239620745126

可以看到 loss 在一点点的下降。当然，这样循环 10 次我们还能观察出来，但是我们如果要成百上千次的去计算它，这样可就不行了，那我们需要将 history 存下来，然后用图来显示出来：

1
2
3
4
5
6
7
8
9
loss_history = []
for _ in range(100):
    ...
    _loss_node = sorted_nodes[-1]
    assert isinstance(_loss_node, Loss)
    loss_history.append(_loss_node.value)
    optimize(sorted_nodes, learning_rate=1e-1)

plt.plot(loss_history)

Alt text

我们现在可以验证一下，我们拟合的 yhat 和真实的 y 之间差距有多大，首先我们当然是要获取到每个值的下标，然后用 sigmoid 函数来算一下：

1
2
3
4
sorted_nodes

---
[k, y, x, b, Linear, Sigmoid, Loss]

通过下标来进行计算，k 是 0，x 是 2，b 是 3，y 是 1：

1
2
3
4
5
6
7
8
9
10
11
12
13
def sigmoid(x):
    return 1/(1+np.exp(-x))

# k*x+b
sigmoid_x = sorted_nodes[0].value * sorted_nodes[2].value + sorted_nodes[3].value
print(sigmoid(sigmoid_x))

# y
print(sorted_nodes[1].value)

---
0.891165479601981
0.8988713384533658

可以看到，非常的接近。那说明我们拟合的情况还是不错的。

好，这里总结一下，就是我们有了拓朴排序，就能向前去计算它的值，通过向前计算的值就可以向后计算它的值。那现在其实我们已经完成了一个 mini 的深度学习框架的核心内容，咱们能够定义节点，能够前向传播运算，能够反向传播运算，能更新梯度了。

那接下来是不是就结束了呢？很遗憾，并没有，接着咱们还要考虑如何处理多维数据。咱们现在看到的数据都是 x、k、b 的输入，也就是都是一维的。

然而咱们真实世界中大多数场景下其实都是多维度的，其实都是多维数组。那么多维数组的还需要更新些什么，和现在有什么区别呢？

我们来接着往后看，因为基本上写法和现在这些几乎完全一样，那我也就不这么细致的讲了。

为了和之前代码做一个区分，所以我将多维向量计算的代码从新开了个文件，放在了23.ipynb里，小伙伴可以去下载到本地研习。

那么多维和现在最大的区别在哪里呢？就在于计算的时候，我们就要用到矩阵运算了。只是值变成了矩阵，运算变成的了矩阵运算。好，我们从 Node 开始来改动它，没什么变化的地方我就直接用...来省略了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
class Node:
    def __init__(self, input=[]):
        ...
    def forward(self):
        raise NotImplemented
    def backward(self):
        raise NotImplemented

class Placeholder(Node):
    def __init__(self):
        Node.__init__(self)
    def forward(self, value=None):
        ...
    def backward(self):
        self.gradients = {self:0}
        for n in self.outputs:
            grad_cost = n.gradients[self]
            self.gradients[self] = grad_cost * 1

class Linear(Node):
    def __init__(self, x, k, b):
        ...
    def forward(self):
        ...
    def backward(self):
        self.gradients = {n: np.zeros_like(n.value) for n in self.inputs}

        for n in self.outputs:
            grad_cost = n.gradients[self]

            self.gradients[self.inputs[0]] = np.dot(grad_cost, self.inputs[1].value.T)
            self.gradients[self.inputs[1]] = np.dot(self.inputs[0].value.T, grad_cost)
            self.gradients[self.inputs[2]] = np.sum(grad_cost, axis=0, keepdims=False)

class Sigmoid(Node):
    def __init__(self, node):
        Node.__init__(self, [node])
    def _sigmoid(self, x):
        ...
    def forward(self):
        ...

    def backward(self):
        self.partial = self._sigmoid(self.x) * (1 - self._sigmoid(self.x))
        self.gradients = {n: np.zeros_like(n.value) for n in self.inputs}
        for n in self.outputs:
            grad_cost = n.gradients[self]  
            self.gradients[self.inputs[0]] = grad_cost * self.partial

class MSE(Node): # 也就是之前的 Loss 类
    def __init__(self, y, a):
        Node.__init__(self, [y, a])
    def forward(self):
        y = self.inputs[0].value.reshape(-1, 1)
        a = self.inputs[1].value.reshape(-1, 1)
        assert(y.shape == a.shape)
        self.m = self.inputs[0].value.shape[0]
        self.diff = y - a
        self.value = np.mean(self.diff**2)
    def backward(self):
        self.gradients[self.inputs[0]] = (2 / self.m) * self.diff
        self.gradients[self.inputs[1]] = (-2 / self.m) * self.diff

类完成之后，我们还有一些其他的方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def forward_and_backward(graph): # run_one_epoch
    for n in graph:
        n.forward()
    for n in  graph[::-1]:
        n.backward()
def toplogic(graph):
    ...
def convert_feed_dict_to_graph(feed_dict):
    ...
# 将 sorted_nodes 赋值从新定义了一个方法
def topological_sort_feed_dict(feed_dict):
    graph = convert_feed_dict_to_graph(feed_dict)
    return toplogic(graph)

def optimize(trainables, learning_rate=1e-2):
    for node in trainables:
        node.value += -1 * learning_rate * node.gradients[node]

这样就完成了。可以发现基本上代码没有什么变动，变化比较大的都是各个类中的 backward 方法，因为要将其变成使用矩阵运算。

我们来尝试着用一下这个多维算法，我们还是用波士顿房价的那个数据来做一下尝试：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
X_ = data['data']
y_ = data['target']

# Normalize data
X_ = (X_ - np.mean(X_, axis=0)) / np.std(X_, axis=0)

n_features = X_.shape[1]
n_hidden = 10
W1_ = np.random.randn(n_features, n_hidden)
b1_ = np.zeros(n_hidden)
W2_ = np.random.randn(n_hidden, 1)
b2_ = np.zeros(1)

# Neural network
X, y = Placeholder(), Placeholder()
W1, b1 = Placeholder(), Placeholder()
W2, b2 = Placeholder(), Placeholder()

l1 = Linear(X, W1, b1)
s1 = Sigmoid(l1)
l2 = Linear(s1, W2, b2)
cost = MSE(y, l2)

feed_dict = {
    X: X_,
    y: y_,
    W1: W1_,
    b1: b1_,
    W2: W2_,
    b2: b2_
}

epochs = 5000
# Total number of examples
m = X_.shape[0]
batch_size = 16
steps_per_epoch = m // batch_size

graph = topological_sort_feed_dict(feed_dict)
trainables = [W1, b1, W2, b2]

print("Total number of examples = {}".format(m))

我们在中间定义了 l1, s1, l2, cost, 分别来实例化四个类。然后我们就需要根据数据来进行迭代计算了，定义一个 losses 来保存历史数据：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
losses = []

epochs = 100

for i in range(epochs):
    loss = 0
    for j in range(steps_per_epoch):
        # Step 1
        X_batch, y_batch = resample(X_, y_, n_samples=batch_size)

        X.value = X_batch
        y.value = y_batch

        # Step 2
        forward_and_backward(graph) # set output node not important.

        # Step 3
        rate = 1e-2
    
        optimize(trainables, rate)

        loss += graph[-1].value
    
    if i % 100 == 0: 
        print("Epoch: {}, Loss: {:.3f}".format(i+1, loss/steps_per_epoch))
        losses.append(loss/steps_per_epoch)

---
Epoch: 1, Loss: 194.170
...
Epoch: 4901, Loss: 3.137

可以看到它 loss 下降的非常快，还记得咱们刚开始的时候在训练波士顿房价数据的时候，那个 loss 下降到多少？最低是不是就下降到在第一节课的时候我们的 lose 最多下降到了多少 47.34 对吧？那现在呢？直接下降到了 3，这是为什么？因为我们的维度多了，维度多了它就准确了。这说明什么？说明大家去谈恋爱的时候，不要盯着对象的一个方面，多方面考察，才能知道这个人是否合适。

好，现在看起来效果是很好，但是我们想知道到底拟合出来的什么函数，那怎么办？咱们把这个维度降低成三维空间就可以看了。

现在咱们这个波士顿的所有数据实际上是一个 15 维的数据，15 维的数据你根本看不了，咱们现在只要把 x 这个里边取一点值，在这个里边稍微把值给它变一下。

1
2
X_ = dataframe[['RM', 'LSTAT']]
y_ = data['target']

在咱们之前的课程中对其进行计算的时候就分析过，RM 和 LSTAT 是影响最大的两个特征，我们还是来用这个。然后我们将刚才的代码从新运行一遍：

1
2
3
4
5
6
7
8
9
losses = []

for i in tqdm_notebook(range(epochs)):
    ...

---
Epoch: 1, Loss: 150.122
...
Epoch: 4901, Loss: 16.181

这次下降的就没上次好了。

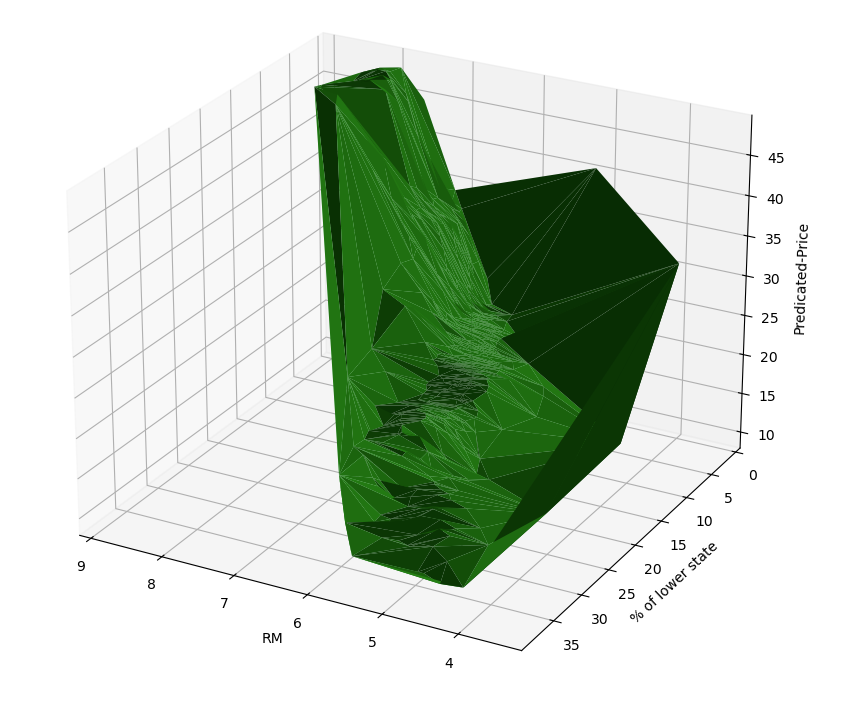
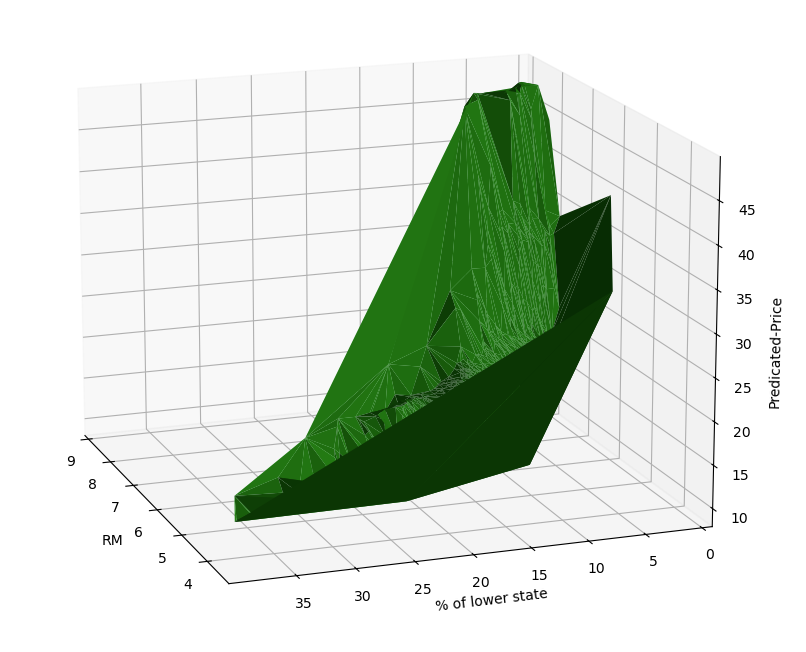
现在我们可视化一下这个三维空间来看看：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from mpl_toolkits.mplot3d import Axes3D

predicate_results = []
for rm, ls in X_.values:
    X.value = np.array([[rm, ls]])
    forward_and_backward(graph)
    predicate_results.append(graph[-2].value[0][0])

%matplotlib widget

fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d')

X_ = dataframe[['RM', 'LSTAT']].values[:, 0]
Y_ = dataframe[['RM', 'LSTAT']].values[:, 1]

Z = predicate_results

rm_and_lstp_price = ax.plot_trisurf(X_, Y_, Z, color='green')

ax.set_xlabel('RM')
ax.set_ylabel('% of lower state')
ax.set_zlabel('Predicated-Price')

然后我们就能看到一个数据的三维图形，因为我们开启了 widget，所以可以进行拖动。

Alt text

Alt text

从图形上看，确实符合房间越多，低收入人群越少，房价越高的特性。

那现在计算机确实帮我们自动的去找到了一个函数，这个函数到底怎么设置咱们都不用关心，它自动就给你求解出来，这个就是深度学习的意义。咱们经过这一系列写出来的东西其实就已经能够做到。

我觉得这个真的有一种数学之美，它从最简单的东西出发，最后做成了这样一个复杂的东西。确实很深其，并且还都在我们的掌握之中。

好，大家下来以后记得要多多自己敲代码，多分析其中的一些过程和原理。

23. 深度学习 - 多维向量自动求导

https://hivan.me/23. 深度学习 - 完成神经网络框架/

作者

Hivan Du

发布于

2023-11-22

更新于

2024-01-16

许可协议

#

喜欢这篇文章？打赏一下作者吧

评论

关注我

链接

分类

最新文章

×