Numba 的 CUDA 示例（1/4）：踏上并行之旅

按照本系列从头开始使用 Python 学习 CUDA 编程

介绍

GPU（图形处理单元），顾名思义，最初是为计算机图形学开发的。从那时起，它们几乎在每个需要高计算吞吐量的领域都无处不在。这一进步得益于 GPGPU（通用 GPU）接口的发展，这些接口使我们能够对 GPU 进行编程以进行通用计算。这些接口中最常见的是CUDA，其次是OpenCL，最近的是 HIP。

Python 中的 CUDA

CUDA 最初设计为与 C 兼容。后来的版本将其扩展到 C++ 和 Fortran。在 Python 生态系统中，使用 CUDA 的方法之一是通过Numba，这是一个适用于 Python 的即时 (JIT) 编译器，可以针对 GPU（它也针对 CPU，但这超出了我们的范围）。使用 Numba，可以直接用 Python（一个子集）编写内核，Numba 将即时编译代码并运行它。虽然它没有实现完整的 CUDA API，但其支持的功能通常足以获得与 CPU 相比令人印象深刻的加速（有关所有缺失的功能，请参阅Numba 文档¹）。

然而， Numba并不是唯一的选择。CuPy既提供依赖于 CUDA 的高级函数，也提供用于集成用 C 编写的内核的低级 CUDA 支持，以及可 JIT 的 Python 函数（类似于 Numba）。PyCUDA 提供了对 CUDA API 的更细粒度控制。最近，Nvidia 发布了官方CUDA Python，这必将丰富生态系统。所有这些项目都可以相互传递设备数组，你不必局限于只使用一个。

在本系列中

本系列的目标是通过用 Numba CUDA 编写的示例为常见的 CUDA 模式提供一个学习平台。本系列并不是 CUDA 或 Numba 的综合指南。读者可以参考它们各自的文档。本教程的结构受到Jason Sanders 和 Edward Kandrot 合著的「 [CUDA by Example: An Introduction to General-Purpose GPU Programming](https://developer.nvidia.com/cuda-example)」一书的启发。如果你最终不再使用 Python 并想用 C 语言编写代码，那么这是一个极好的资源。

本系列还将会包含第 2 部分、第 3 部分和第 4 部分。

在本教程中，我们将学习如何运行我们的第一个 Numba CUDA 内核。我们还将学习如何有效地使用 CUDA 执行高度并行的任务，即完全相互独立的任务。最后，我们将学习如何从 CPU 计时内核的运行时间。因为我的电脑是 Mac，无法实现 CUDA，所以我在 Google Colab 上进行了实现，可以点击查看：https://colab.research.google.com/drive/1O5bhDHZgJqLwVaQl4rkoewY_XyO_krKQ?usp=sharing

GPU 并行编程简介

GPU 相对于 CPU 的最大优势在于它们能够并行执行相同的指令。单个 CPU 内核将以串行方式一个接一个地运行指令。在 CPU 上进行并行化需要同时使用其多个内核（物理或虚拟）。标准的现代计算机具有 4-8 个内核。另一方面，现代 GPU 拥有数百甚至数千个计算内核。参见图 1 以了解两者之间的比较。GPU 内核通常较慢并且只能执行简单指令，但它们的庞大数量通常可以弥补这些缺点。需要注意的是，为了使 GPU 比 CPU 更具优势，它们运行的算法必须是可并行的。

我认为理解 GPU 编程有四个主要方面。第一个我已经提到过：理解如何思考和设计本质上并行的算法。这可能很难，因为有些算法是串行设计的，也因为可以有多种并行化同一算法的方法。

第二个方面是学习如何将主机上的结构（例如矢量和图像）映射到 GPU 结构（例如线程和块）上。重复模式和辅助函数可以帮助我们实现这一点，但归根结底，实验对于充分利用 GPU 至关重要。

第三是理解驱动 GPU 编程的异步执行模型。不仅 GPU 和 CPU 彼此独立地执行指令，GPU 还具有允许多个处理流在同一 GPU 中运行的流。这种异步性在设计最佳处理流程时非常重要。

第四个也是最后一个方面是抽象概念和具体代码之间的关系：这是通过学习 API 及其细微差别来实现的。

当你阅读第一章时，请尝试在以下示例中识别这些概念！

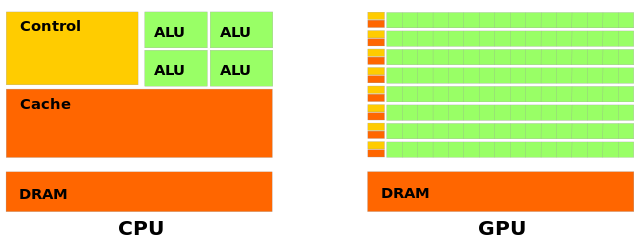
图 1.1。简化的 CPU 架构（左）和 GPU 架构（右）。算术发生在 ALU（算术逻辑单元）中，DRAM 数据，缓存保存可以更快访问的数据，但通常容量较小。控制单元执行指令。来源：维基百科。

入门

我们将首先设置我们的环境：高于 0.55 的 Numba 版本和受支持的 GPU。

import numpy as np
import numba
from numba import cuda

print(np.__version__)
print(numba.__version__)

---
1.25.2
0.59.1


cuda.detect()

---
Found 1 CUDA devices
id 0             b'Tesla T4'                              [SUPPORTED]
                      Compute Capability: 7.5
                           PCI Device ID: 4
                              PCI Bus ID: 0
                                    UUID: GPU-0aa3c43c-1ada-6075-e57a-dccb0793a8b6
                                Watchdog: Disabled
             FP32/FP64 Performance Ratio: 32
Summary:
	1/1 devices are supported
True

Numba CUDA 的主要工作是cuda.jit装饰器。它用于定义将在 GPU 中运行的函数。

我们首先定义一个简单的函数，该函数接受两个数字并将它们存储在第三个参数的第一个元素上。我们的第一课是内核（启动线程的 GPU 函数）不能返回值。我们通过传递输入和输出来解决这个问题。这是 C 中的常见模式，但在 Python 中并不常见。

# Example 1.1: Add scalars
@cuda.jit
def add_scalars(a, b, c):
    c[0] = a + b

dev_c = cuda.device_array((1,), np.float32)

add_scalars[1, 1](2.0, 7.0, dev_c)

c = dev_c.copy_to_host()
print(f"2.0 + 7.0 = {c[0]}")

---
2.0 + 7.0 = 9.0

你可能已经注意到，在调用内核之前，我们需要在设备上分配一个数组。此外，如果我们想显示返回的值，我们需要将其复制回 CPU。你可能会问自己为什么我们选择分配一个float32（单精度浮点数）。这是因为，虽然大多数现代 GPU 都支持双精度运算，但双精度运算所需的时间可能是单精度运算的 4 倍或更长。因此，最好习惯使用np.float32andnp.complex64而不是float/np.float64和complex/ np.complex128。

虽然内核定义看起来类似于 CPU 函数，但内核调用略有不同。特别是，它在参数前有方括号：

add_scalars[1, 1](2.0, 7.0, dev_c)

这些方括号分别表示网格中的块数和块中的线程数。在学习使用 CUDA 进行并行化时，让我们进一步讨论一下这些含义。

使用 CUDA 进行并行化

CUDA 网格的剖析

启动内核时，它会有一个与之关联的网格。网格由块组成；块由线程组成。图 2 显示了一维 CUDA 网格。图中的网格有 4 个块。网格中的块数保存在一个特殊变量中，该变量可在内核内部访问，称为gridDim.x。.x是指网格的第一维（在本例中是唯一的一维）。二维网格也有.y和三维网格.z变量。同样在内核内部，你可以通过使用 找出正在执行哪个块blockIdx.x，在本例中它将从 0 运行到 3。

每个块都有一定数量的线程，保存在变量中blockDim.x。线程索引保存在变量中threadIdx.x，在本例中从 0 到 7。

重要的是，不同块中的线程被安排以不同的方式运行，可以访问不同的内存区域，并且在某些方面也有所不同（请参阅CUDA 复习：CUDA 编程模型的简要讨论）。现在，我们将跳过这些细节。

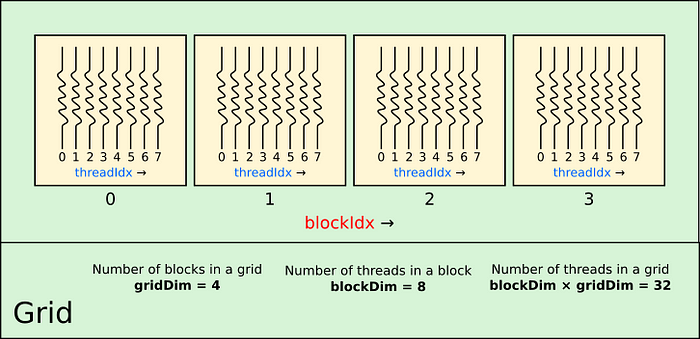
当我们在第一个示例中使用参数启动内核时[1, 1]，我们告诉 CUDA 运行一个块和一个线程。传递多个块和多个线程将多次运行内核。操纵threadIdx.x和blockIdx.x将使我们能够唯一地标识每个线程。

我们不再对两个数字求和，而是尝试对两个数组求和。假设每个数组有 20 个元素。如上图所示，我们可以启动一个内核，每个块有 8 个线程。如果我们希望每个线程只处理一个数组元素，那么我们将至少需要 4 个块。启动 4 个块，每个块有 8 个线程，我们的网格将启动 32 个线程。

现在我们需要弄清楚如何将线程索引映射到数组索引。threadIdx.x从 0 到 7 运行，因此它们本身无法索引我们的数组。此外，不同的块具有相同的threadIdx.x。另一方面，它们具有不同的blockIdx.x。要为每个线程获取唯一索引，我们可以组合这些变量：

i = threadIdx.x + blockDim.x * blockIdx.x

对于第一个块，blockIdx.x = 0和i将从 0 运行到 7。对于第二个块，blockIdx.x = 1。由于blockDim.x = 8，i将从 8 运行到 15。同样，对于blockIdx.x = 2，i将从 16 运行到 23。在第四个也是最后一个块中，i将从 24 运行到 31。请参阅下表 1。

i	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	...	31
threadIdx.x	0	1	2	3	4	5	6	7	0	1	2	3	4	5	6	7	0	...	7
blockIdx.x	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	2	...	3

我们解决了一个问题：如何将每个线程映射到数组中的每个元素……但现在我们遇到了一个问题，即某些线程会溢出数组，因为数组有 20 个元素，最多i可达 32-1。解决方案很简单：对于这些线程，不要执行任何操作！

我们来看看代码。

# Example 1.2: Add arrays
@cuda.jit
def add_array(a, b, c):
    i = cuda.threadIdx.x + cuda.blockDim.x * cuda.blockIdx.x
    if i < a.size:
        c[i] = a[i] + b[i]

N = 20
a = np.arange(N, dtype=np.float32)
b = np.arange(N, dtype=np.float32)
dev_c = cuda.device_array_like(a)

add_array[4, 8](a, b, dev_c)

c = dev_c.copy_to_host()
print(c)

---
[ 0.  2.  4.  6.  8. 10. 12. 14. 16. 18. 20. 22. 24. 26. 28. 30. 32. 34. 36. 38.]

在较新版本的 Numba 中，我们会收到一条警告，指出我们使用主机数组调用了内核。理想情况下，我们希望避免将数据从主机移动到设备，因为这非常慢。我们应该在所有参数中使用设备数组调用内核。我们可以通过预先将数组从主机移动到设备来实现这一点：

dev_a = cuda.to_device（a）
dev_b = cuda.to_device（b）

此外，每个线程的唯一索引的计算很快就会过时。值得庆幸的是，Numba 提供了非常简单的包装器cuda.grid，它以网格维度作为唯一参数来调用。新内核将如下所示：

# Example 1.3: Add arrays with cuda.grid
@cuda.jit
def add_array(a, b, c):
    i = cuda.grid(1)
    if i < a.size:
        c[i] = a[i] + b[i]

add_array[4, 8](dev_a, dev_b, dev_c)

c = dev_c.copy_to_host()
print(c)

---
[ 0.  2.  4.  6.  8. 10. 12. 14. 16. 18. 20. 22. 24. 26. 28. 30. 32. 34. 36. 38.]

当我们改变数组的大小时会发生什么？一种简单的解决方法是简单地更改网格参数（块数和每个块的线程数），以便至少启动与数组中的元素一样多的线程。

设置这些参数既需要一定的科学性，也需要一定的艺术性。从“科学性”的角度来说，我们会说 (a) 它们应该是 2 的倍数，通常在 32 到 1024 之间，以及 (b) 应该选择它们以最大化占用率（同时有多少个线程处于活动状态）。Nvidia 提供了一个电子表格来帮助计算这些值。从“艺术性”的角度来说，没有什么可以预测内核的行为，因此如果你真的想优化这些参数，你需要使用典型输入来分析你的代码。实际上，现代 GPU 的“合理”线程数是 256。

N = 1_000_000
a = np.arange(N, dtype=np.float32)
b = np.arange(N, dtype=np.float32)

dev_a = cuda.to_device(a)
dev_b = cuda.to_device(b)
dev_c = cuda.device_array_like(a)

threads_per_block = 256
blocks_per_grid = (N + (threads_per_block - 1)) // threads_per_block
# Note that
#     blocks_per_grid == ceil(N / threads_per_block)
# ensures that blocks_per_grid * threads_per_block >= N

add_array[blocks_per_grid, threads_per_block](dev_a, dev_b, dev_c)

c = dev_c.copy_to_host()
np.allclose(a + b, c)

---
True

在继续讨论向量求和之前，我们需要讨论一下硬件限制。GPU 无法运行任意数量的线程和块。通常，每个块不能有超过 1024 个线程，并且网格不能有超过 2¹⁶ − 1 = 65535 个块。这并不是说你可以启动 1024 × 65535 个线程……根据其寄存器占用的内存量以及其他考虑因素，可以启动的线程数量是有限制的。此外，必须谨慎尝试处理无法一次性放入 GPU RAM 的大型数组。在这些情况下，可以使用单个 GPU 或多个 GPU 分段处理数组。

信息：在 Python 中，可以通过 Nvidia 的 cuda-python 库，通过其文档中的函数 cuDeviceGetAttribute 获取硬件限制。有关示例，请参见本节末尾的附录。

网格跨步循环

如果每个网格的块数超出硬件限制，但数组适合内存，则我们可以使用一个线程来处理多个元素，而不是每个数组元素使用一个线程。我们将使用一种称为网格步长循环的技术来实现这一点。除了克服硬件限制之外，网格步长循环内核还可以通过重用线程来最大限度地减少线程创建/销毁开销。Mark Harris 的博客文章 CUDA Pro Tip: Write Flexible Kernels with Grid-Stride Loops 详细介绍了网格步长循环的一些好处。

该技术背后的想法是在 CUDA 内核中添加一个循环来处理多个输入元素。顾名思义，此循环的步幅等于网格中的线程数。这样，如果网格中的线程总数 ( threads_per_grid = blockDim.x * gridDim.x) 小于数组元素的数量，则内核处理完索引后cuda.grid(1)就会处理索引cuda.grid(1) + threads_per_grid，依此类推，直到处理完所有数组元素。事不宜迟，让我们看看代码。

# Example 1.4: Add arrays with grid striding
@cuda.jit
def add_array_gs(a, b, c):
    i_start = cuda.grid(1)
    threads_per_grid = cuda.blockDim.x * cuda.gridDim.x
    for i in range(i_start, a.size, threads_per_grid):
        c[i] = a[i] + b[i]

threads_per_block = 256
blocks_per_grid_gs = 32 * 80  # Use 32 * multiple of streaming multiprocessors
# 32 * 80 * 256 < 1_000_000 so one thread will process more than one array element

add_array_gs[blocks_per_grid_gs, threads_per_block](dev_a, dev_b, dev_c)
c = dev_c.copy_to_host()
np.allclose(a + b, c)

---
True

这段代码与上面的代码非常相似，不同之处在于我们从 cuda.grid(1) 开始，但会执行更多的采样，每个threads_per_grid 执行一次，直到数组结束。

那么，哪一个内核更快呢？

计时 CUDA 内核

GPU 编程的核心在于速度。因此，准确测量代码执行情况非常重要。

CUDA 内核是主机 (CPU)启动的设备功能，但它们当然是在 GPU 上执行的。除非我们告诉它们，否则 GPU 和 CPU 不会进行通信。因此，当 GPU 内核启动时，CPU 将继续运行指令，无论是启动更多内核还是执行其他 CPU 功能。如果我们time.time()在内核启动之前和之后进行调用，我们将仅计时内核启动所需的时间，而不是运行所需的时间。

我们可以使用一个函数来确保 GPU 已经“赶上” 。cuda.synchronize()，调用此函数将停止主机执行任何其他代码，直到 GPU 完成已在其中启动的每个内核的执行。

要对内核执行进行计时，我们可以简单地计时内核运行然后同步所需的时间。这有两个注意事项。首先，我们需要使用time.perf_counter()或time.perf_counter_ns()而不是time.time()。time.time()不计算主机休眠等待 GPU 完成执行的时间。第二个注意事项是，从主机计时代码并不理想，因为这会产生相关开销。稍后，我们将解释如何使用 CUDA事件对来自设备的内核进行计时。Mark Harris 有另一篇关于此主题的精彩博客文章，标题为How to Implement Performance Metrics in CUDA C/C++。

使用 Numba 时，我们必须注意一个细节。Numba 是一个即时编译器，这意味着函数只有在被调用时才会被编译。因此，对函数的第一次调用进行计时也会对编译步骤进行计时，而编译步骤通常要慢得多。我们必须记住始终先通过启动内核然后同步它来编译代码，以确保 GPU 中没有剩余的内容要运行。这可确保下一个内核无需编译即可立即运行。还要注意，数组的dtype应该相同，因为 Numba 为参数的每种组合编译一个唯一的函数dtypes。

from time import perf_counter_ns

# Compile and then clear GPU from tasks
add_array[blocks_per_grid, threads_per_block](dev_a, dev_b, dev_c)
cuda.synchronize()

timing = np.empty(101)
for i in range(timing.size):
    tic = perf_counter_ns()
    add_array[blocks_per_grid, threads_per_block](dev_a, dev_b, dev_c)
    cuda.synchronize()
    toc = perf_counter_ns()
    timing[i] = toc - tic
timing *= 1e-3  # convert to μs

print(f"Elapsed time: {timing.mean():.0f} ± {timing.std():.0f} μs")

---
Elapsed time: 131 ± 36 μs

# Compile and then clear GPU from tasks
add_array_gs[blocks_per_grid_gs, threads_per_block](dev_a, dev_b, dev_c)
cuda.synchronize()

timing_gs = np.empty(101)
for i in range(timing_gs.size):
    tic = perf_counter_ns()
    add_array_gs[blocks_per_grid_gs, threads_per_block](dev_a, dev_b, dev_c)
    cuda.synchronize()
    toc = perf_counter_ns()
    timing_gs[i] = toc - tic
timing_gs *= 1e-3  # convert to μs

print(f"Elapsed time: {timing_gs.mean():.0f} ± {timing_gs.std():.0f} μs")

---
Elapsed time: 140 ± 36 μs

对于简单内核，我们还可以测量算法的吞吐量，它等于每秒浮点运算次数。它通常以 GFLOP/s（每秒千兆 FLOP）为单位。我们的加法运算仅包含一个 FLOP：加法。因此，吞吐量由以下公式给出：

#              G * FLOP       / timing in s
gflops    = 1e-9 * dev_a.size * 1e6 / timing.mean()
gflops_gs = 1e-9 * dev_a.size * 1e6 / timing_gs.mean()

print(f"GFLOP/s (algo 1): {gflops:.2f}")
print(f"GFLOP/s (algo 2): {gflops_gs:.2f}")

---
GFLOP/s (algo 1): 7.65
GFLOP/s (algo 2): 7.15

2D 示例

为了结束本教程，让我们制作一个 2D 内核来对图像应用对数校正。

给定一个图像 I(x, y)，其值介于 0 和 1 之间，对数校正图像由下式给出

Iᵪ(x, y) = γ log₂ (1 + I(x, y))

首先让我们获取一些数据！

import matplotlib.pyplot as plt
from skimage import data

moon = data.moon().astype(np.float32) / 255.

fig, ax = plt.subplots()
im = ax.imshow(moon, cmap="gist_earth")
ax.set_xticks([])
ax.set_yticks([])
ax.set_xticklabels([])
ax.set_yticklabels([])
fig.colorbar(im)
fig.tight_layout()

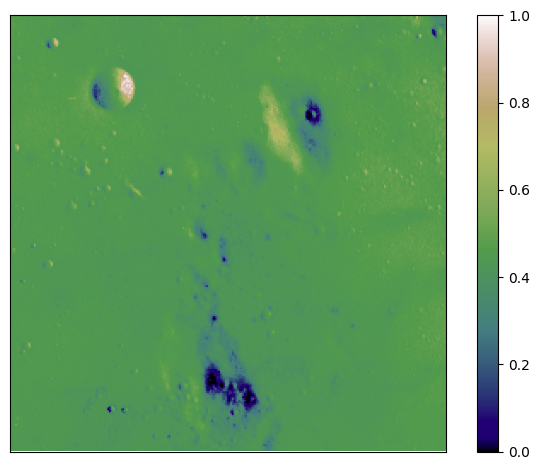
如你所见，数据在低端确实饱和了，几乎没有高于 0.6 的值。

让我们编写内核。

import math

# Example 1.5: 2D kernel
@cuda.jit
def adjust_log(inp, gain, out):
    ix, iy = cuda.grid(2) # The first index is the fastest dimension
    threads_per_grid_x, threads_per_grid_y = cuda.gridsize(2) #  threads per grid dimension
    
    n0, n1 = inp.shape # The last index is the fastest dimension
    # Stride each dimension independently
    for i0 in range(iy, n0, threads_per_grid_y):
        for i1 in range(ix, n1, threads_per_grid_x):
            out[i0, i1] = gain * math.log2(1 + inp[i0, i1])

threads_per_block_2d = (16, 16)  #  256 threads total
blocks_per_grid_2d = (64, 64)

moon_gpu = cuda.to_device(moon)
moon_corr_gpu = cuda.device_array_like(moon_gpu)

adjust_log[blocks_per_grid_2d, threads_per_block_2d](moon_gpu, 1.0, moon_corr_gpu)
moon_corr = moon_corr_gpu.copy_to_host()

fig, (ax1, ax2) = plt.subplots(1, 2)
ax1.imshow(moon, cmap="gist_earth")
ax2.imshow(moon_corr, cmap="gist_earth")
ax1.set(title="Original image")
ax2.set(title="Log-corrected image")
for ax in (ax1, ax2):
    ax.set_xticks([])
    ax.set_yticks([])
    ax.set_xticklabels([])
    ax.set_yticklabels([])
fig.tight_layout()

让我们注意一下这两个 for 循环。请注意，第一个 for 循环从 iy 开始，而最内层的第二个循环从 ix 开始。我们完全可以选择 i0 从 ix 处开始，而 i1 从 iy 处开始，这样会感觉更自然。那么，我们为什么要选择这种顺序呢？事实证明，第一种选择的内存访问模式更有效。由于第一个网格索引是最快的索引，我们希望它能与我们最快的维度（即最后一个维度）相匹配。

如果你不想相信我的话（你不应该相信！）你现在已经学会了如何对内核执行进行计时，你可以尝试这两个版本。对于像这里使用的数组这样的小数组，差异可以忽略不计，但对于较大的数组（例如 10,000 x 10,000），我测量到的速度提高了约 10%。虽然不是特别令人印象深刻，但如果我可以通过一次变量交换为你提供 10% 的改进，谁会不接受呢？

就这样！我们现在可以在校正后的图像中看到更多细节。

作为练习，尝试使用不同的网格对不同的启动进行计时，以找到适合你的机器的最佳网格大小。

结论

在本教程中，你学习了 Numba CUDA 的基础知识。你学习了如何创建简单的 CUDA 内核，并将内存移至 GPU 以使用它们。你还学习了如何使用一种称为grid-stride loops 的技术迭代 1D 和 2D 数组。

附录：使用 Nvidia 的 cuda-python 探测设备属性

为了对 GPU 的精确属性进行细粒度控制，你可以依赖 Nvidia 提供的低级官方 CUDA Python 包。

# Need to: pip install --upgrade cuda-python

from cuda.cuda import CUdevice_attribute, cuDeviceGetAttribute, cuDeviceGetName, cuInit

# Initialize CUDA Driver API
(err,) = cuInit(0)

# Get attributes
err, DEVICE_NAME = cuDeviceGetName(128, 0)
DEVICE_NAME = DEVICE_NAME.decode("ascii").replace("\x00", "")

err, MAX_THREADS_PER_BLOCK = cuDeviceGetAttribute(
    CUdevice_attribute.CU_DEVICE_ATTRIBUTE_MAX_THREADS_PER_BLOCK, 0
)
err, MAX_BLOCK_DIM_X = cuDeviceGetAttribute(
    CUdevice_attribute.CU_DEVICE_ATTRIBUTE_MAX_BLOCK_DIM_X, 0
)
err, MAX_GRID_DIM_X = cuDeviceGetAttribute(
    CUdevice_attribute.CU_DEVICE_ATTRIBUTE_MAX_GRID_DIM_X, 0
)
err, SMs = cuDeviceGetAttribute(
    CUdevice_attribute.CU_DEVICE_ATTRIBUTE_MULTIPROCESSOR_COUNT, 0
)

print(f"Device Name: {DEVICE_NAME}")
print(f"Maximum number of multiprocessors: {SMs}")
print(f"Maximum number of threads per block: {MAX_THREADS_PER_BLOCK:10}")
print(f"Maximum number of blocks per grid:   {MAX_BLOCK_DIM_X:10}")
print(f"Maximum number of threads per grid:  {MAX_GRID_DIM_X:10}")

---
Device Name: Tesla T4                                                                
Maximum number of multiprocessors: 40
Maximum number of threads per block:       1024
Maximum number of blocks per grid:         1024
Maximum number of threads per grid:  2147483647

---

1. https://numba.readthedocs.io/en/stable/cuda/overview.html#missing-cuda-features↩︎