发表AI

使用高斯混合模型识别餐厅热点

原文：https://towardsdatascience.com/identifying-restaurant-hotspots-with-a-gaussian-mixture-model-2a840ab0c782

使用 GMM 识别加拿大多伦多的直观餐厅集群（附 Python 代码）

聚类算法（例如 GMM）是一种有用的工具，可帮助识别数据中的模式。它们使我们能够识别数据集中的子组，从而提高你的理解或增强预测模型。在本文中，借助 GMM，我们将尝试使用位置数据识别多伦多的餐厅集群。目标是找到在地理上合理但在其他特征（例如餐厅评级）方面具有不同特征的集群。我们将讨论关键代码，你可以在GitHub1上找到完整的项目。

img

什么是 GMM

如上所述，GMM 是一种聚类算法。这意味着它可用于根据特征对数据集中的元素进行分组。例如，假设我们有一个客户收入和年龄的数据集。聚类算法可以识别 4 个组：老年高收入者、老年低收入者、年轻高收入者和年轻低收入者。这 4 个群体可能具有非常不同的特征/行为。我们不会详细介绍 GMM 如何创建这些聚类，因为有很多很好的资料来源23。重要的是为什么我们要使用 GMM 而不是其他聚类算法（例如 K-means）。

对于我们的问题，GMM 最重要的优势是它在聚类方差和协方差方面更加灵活。首先，更大的方差灵活性意味着 GMM 可以更好地识别方差不等的聚类。换句话说，当我们既有密集的聚类又有分散的聚类时，它将产生更好的结果。我们可以在下面的图 1 中看到这一点，其中我们将 K-means 和 GMM 应用于一些测试数据。这里每个点的颜色由相关算法分配的聚类决定。在这种情况下，GMM 聚类似乎更合适。

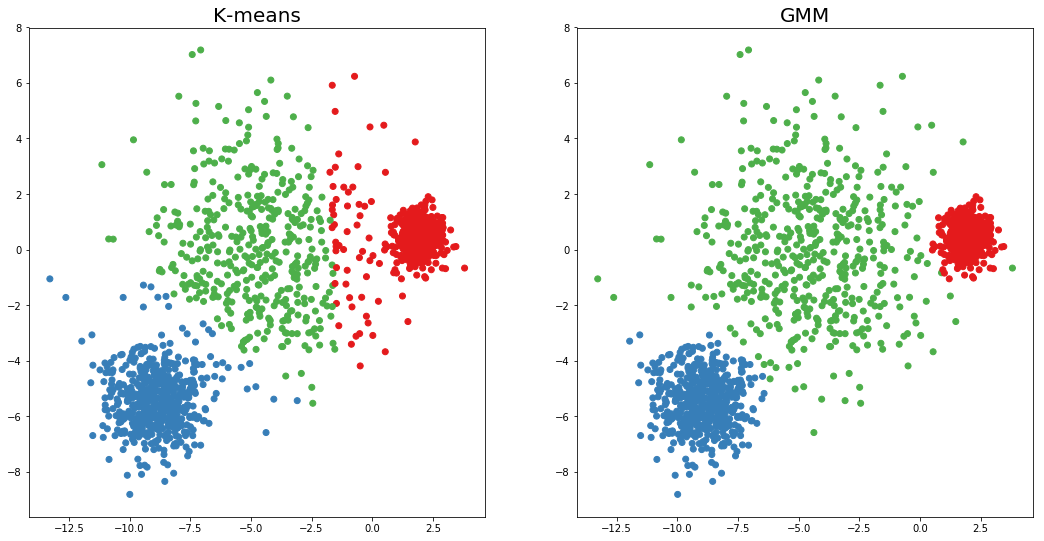
图1：不同方差的聚类算法比较

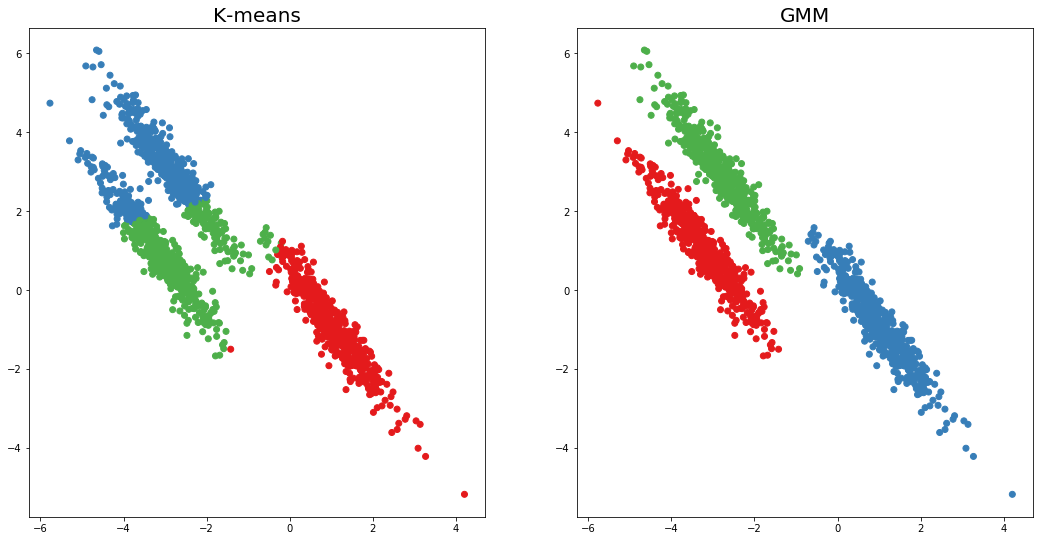
其次，协方差灵活性越高，我们就能识别出更细长/椭圆形的簇。相比之下，K 均值只能真正识别球形簇。我们可以在图 2 中看到这一点，GMM 簇再次更合适。当我们将 GMM 的这些属性应用于我们的餐厅数据集时，我们就会明白为什么它们如此重要。最终，它将使我们能够找到更有趣的簇。

图2：非球形聚类算法比较

数据集

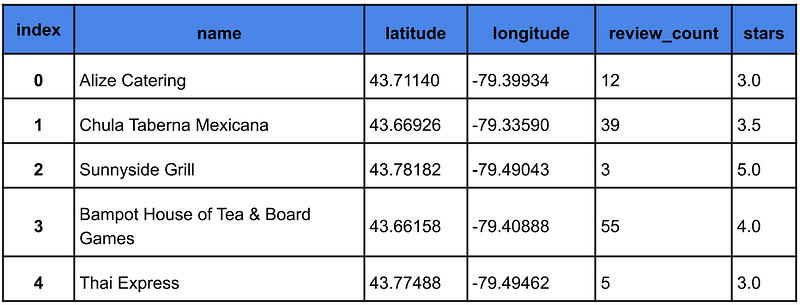
为了训练 GMM，我们将使用 Yelp 开放数据集4餐馆的大量信息。我们对其进行了预处理，以便获得多伦多每家餐馆的名称、纬度和经度。我们还包括评论数量（review_count）和餐馆评级（星级），稍后将用于分析聚类。其他特征（例如餐馆的街区和类别）已被排除。我们使用下面的代码读取数据集，我们可以在表 1 中看到一个示例。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import pandas as pd

data = pd.read_csv(data_path + "/yelp_data/toronto_restaurant.csv",usecols=['name','latitude','longitude','stars','review_count'])
print(len(data))
data.head()

---
7148
	name	latitude	longitude	review_count	stars
0	Alize Catering	43.71140	-79.39934	12	3.0
1	Chula Taberna Mexicana	43.66926	-79.33590	39	3.5
2	Sunnyside Grill	43.78182	-79.49043	3	5.0
3	Bampot House of Tea & Board Games	43.66158	-79.40888	55	4.0
4	Thai Express	43.77488	-79.49462	5	3.0

表 1：餐厅数据集示例

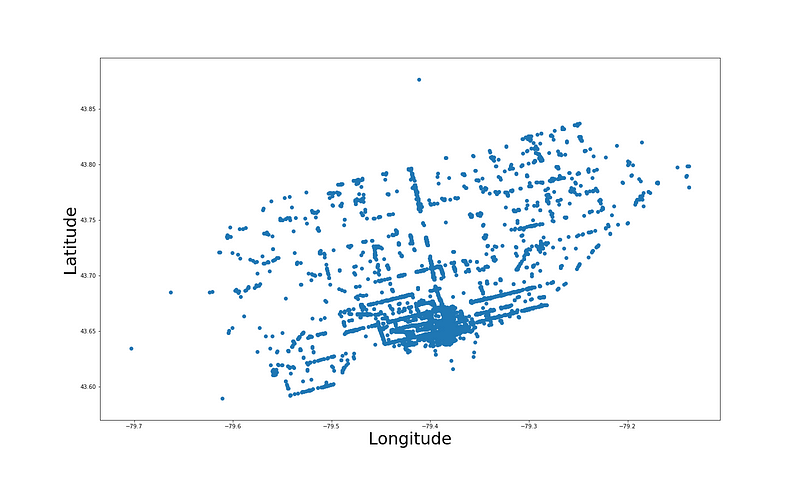
在图 3 中，我们用经纬度标出了所有餐厅。每个点代表一家餐厅，总共有 7148 多家餐厅。餐厅的位置可以告诉我们一些信息。例如，某些位置的餐厅可能评级较高。因此，我们可能能够在试图预测餐厅评级等信息的模型中使用位置。但是，仅输入原始的经纬度数据可能不会给我们带来好的结果——尤其是在使用线性模型的情况下。这意味着我们必须对经纬度特征执行某种形式的特征工程。

3：使用餐厅经纬度的散点图图

在某些方面，考虑到我们有餐厅社区，这已经完成了。换句话说，餐厅已经根据其纬度和经度被分组为集群（即社区）。问题是多伦多有 71 个不同的社区，需要估计很多系数。你可能可以根据某些社区的特点将它们分组在一起，但这需要多伦多餐厅领域的专业知识。我们将尝试一种替代方法，即使用 GMM 对餐厅进行分组。

拟合 GMM

在下面的 Python 函数的第一部分中，我们训练 GMM。GMM 的一个问题是它们会收敛到局部最优点。为了避免这种情况，我们将“n_init”参数设置为 5。这将随机初始化和训练 5 个 GMM，最后，我们将最佳模型作为最终模型。我们使用此模型获得每家餐厅的标签/预测。然后，如图 3 所示，我们绘制餐厅，但这次我们根据 GMM 标签分配颜色。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import sklearn.mixture as sm
import matplotlib.pyplot as plt
%matplotlib inline

def plot_gmm(n):
      """
    Train a GMM and plot the results
    
    Parameters
    ----------
    n : int
        Number of clusters
    """
    
    #Fit gmm and get labels
    x = data[['longitude','latitude']].values
    gmm = sm.GaussianMixture(n_components=n, random_state=11,n_init=5)
    labels = gmm.fit(x).predict(x)
    
    #assign a colour to each label
    colour = ['#f54242','#4287f5','#f59942','#f5f242','#69f542','#b342f5']
    c = [colour[l] for l in labels]
    
    #scatter plot
    plt.figure(figsize=(20, 12))
    plt.scatter(x=x[:, 0], y=x[:, 1], c=c, s=40, cmap='Set1', zorder=1)
    plt.title('Number of Clusters: {}'.format(n),size=25)
    plt.xlabel('Longitude',size=20)
    plt.ylabel('Latitude',size=20)
    
plot_gmm(5)

你可能已经注意到，此函数采用一个参数 — 聚类数。这被视为 GMM 的超参数，我们必须选择它。如果我们决定使用过多的聚类，模型将过度拟合数据。这意味着我们将识别出没有意义的聚类或拆分更适合集中在一起的聚类。如果我们决定使用过少的聚类，模型可能会对数据产生欠拟合。这意味着我们可能会错过一些重要的聚类。问题是我们如何决定聚类的数量？

有几种不同的方法可以帮助确定适当的聚类数量。这些方法包括使用轮廓分数或模型 BIC 值5(https://towardsdatascience.com/gaussian-mixture-model-clusterization-how-to-select-the-number-of-components-clusters-553bef45f6e4)。这些只是有用的指导方针，不一定能为你提供最佳的聚类数量。由于我们仅使用 2 个特征来训练我们的 GMM，因此我们可以轻松地可视化结果并了解聚类是否合适。例如，如图 5 所示，我们使用上面的 Python 函数绘制具有 5 个聚类的 GMM 的结果。

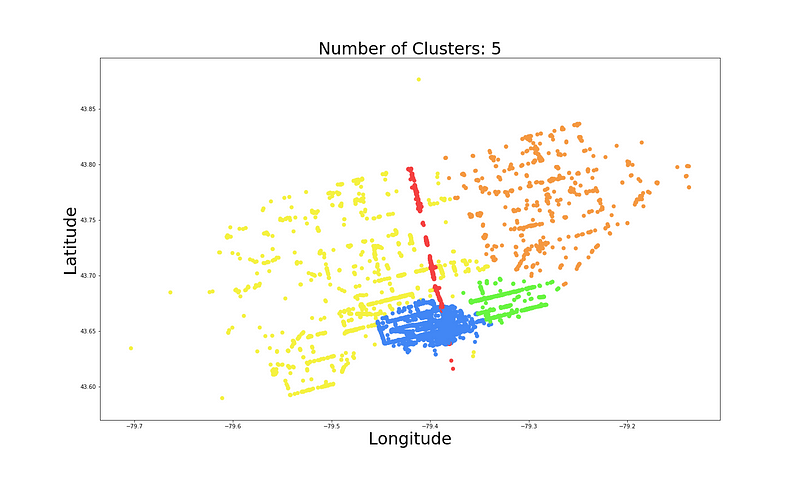
图 5：使用 5 个聚类的 GMM 标签散点图

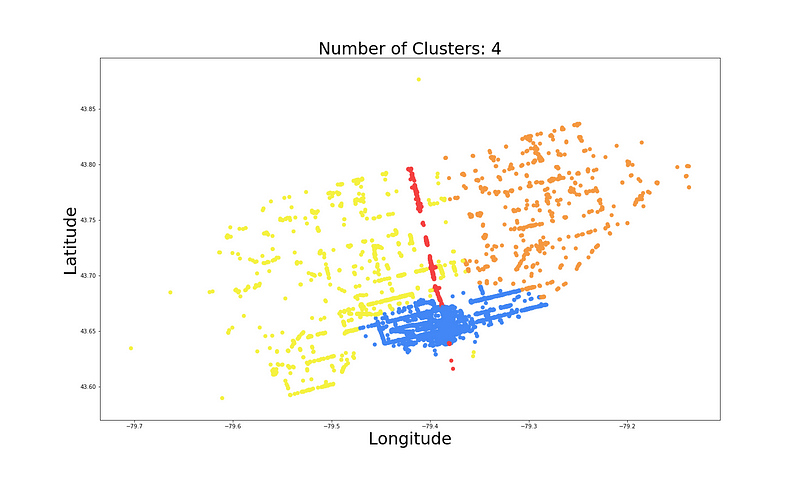
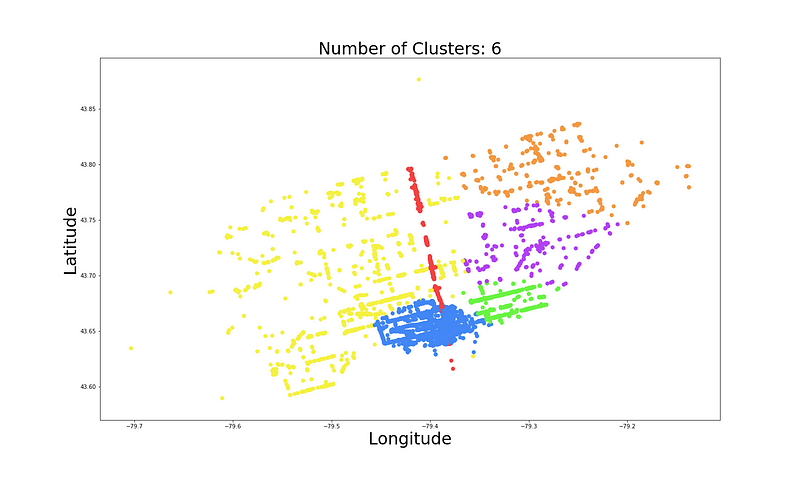
GMM 已识别出一些有趣的聚类。例如，蓝色聚类似乎非常密集，附近有许多餐馆。长红色聚类似乎是一条道路。在图 6 中，我们分别使用 4 个和 6 个聚类看到了类似的图。在这两种情况下，我们都看到 GMM 已识别出与图 5 中类似的聚类。所以，让我们继续使用 5 个聚类。我们可以进一步分析它们，以更好地了解它们是否合适。

img

图 6：使用替代数量的聚类的 GMM 标签散点图

分析集群

如果我们看一下多伦多的地图，我们可以更好地理解这些集群。我们使用下面的代码来做到这一点。首先，我们从具有 5 个集群的 GMM 中获取标签。然后我们创建一个以多伦多为中心的叶状图。最后，我们将每个点叠加在地图上。像以前一样，每个点的颜色由其标签决定。我们可以在图 7 中看到这个过程的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import folium

#Get gmm predictions
x = data[['longitude','latitude']].values
gmm = sm.GaussianMixture(n_components=5, random_state=11,n_init=5)
labels = gmm.fit(x).predict(x)

#create folium map 
m = folium.Map(
    location=[43.77923, -79.41731999999998],
    zoom_start=12,
    tiles='Stamen Terrain'
)

colour = ['#f54242','#4287f5','#f59942','#f5f242','#69f542','#b342f5']

#add markers to map 
for i in range(len(x)):
    lon = x[i][0]
    lat = x[i][1]
    label = labels[i]
    
    #assign colour based on label 
    c = colour[label]
    
    #add marker
    folium.CircleMarker(location=[lat,lon],
                        radius=2,
                        color=c,
                        fill_color=c).add_to(m) 

#display map
m

看一看地图，这些聚类开始变得更有意义了。蓝色和绿色聚类位于多伦多港周围人口更密集的城市地区。这些聚类大致被一条高速公路隔开，这似乎是划分餐厅群体的相当自然的方式。黄色和橙色聚类密度较低，它们由郊区的餐厅组成。长长的红色聚类特别有趣。几乎所有这些点都落在央街上。快速搜索显示，这实际上是多伦多最著名的街道。考虑到这一点，将这些餐厅归入自己的组是有意义的。

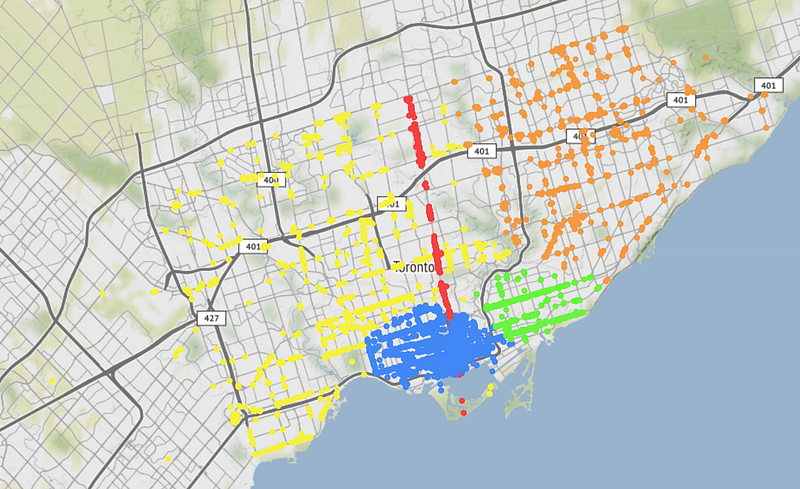
图 7：GMM 聚类覆盖多伦多地图

这些聚类并不完美。有一些不规则的红点可能适合成为蓝色聚类的一部分。同样，高速公路右侧的一些蓝点可能应该属于绿色聚类。在很大程度上，GMM 已经识别出在地理上有意义的聚类。我们可以预期它们具有不同的特征，但事实并非如此。

我们可以通过考虑餐厅的评论和评分来研究这些特征。在表 2 中，我们可以看到每个集群中餐厅的平均评论数量。我们看到蓝色集群中的评论数量往往更高。事实上，平均评论数量是黄色和橙色集群的两倍多。这可能是有道理的，因为我们可以预期密集地区的餐厅会有更多的顾客。

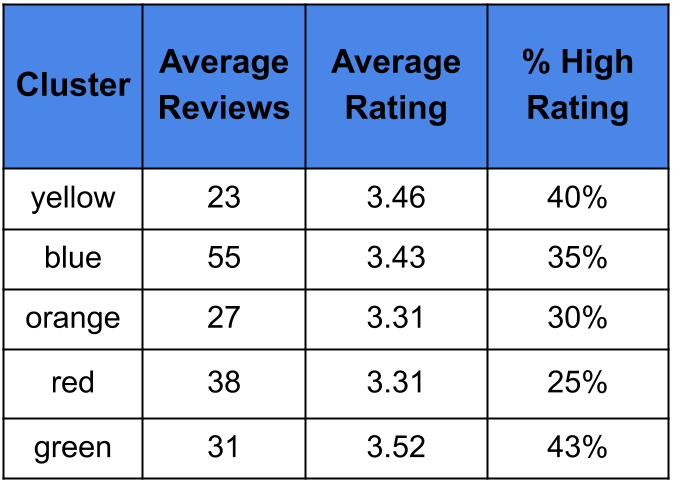
表 2：集群评审和评级分析

我们还可以看到平均评分和至少有 4 星评分的餐厅百分比（高评分百分比）。绿色集群中的餐厅平均评分最高，高评分餐厅比例最高。也许这是多伦多一个更高档的地区？同样在评分方面，两个郊区集群（黄色和橙色）往往相差很大。

这只是我们可以用来比较聚类的两个特征。我们可以一直分析下去。归根结底，聚类的适用性取决于你想用它们做什么。一般的想法是，也许经过一些微调后，你可以用它的聚类来标记每家餐厅，并将其用作分析或模型中的一个特征。你也可以使用这些聚类作为类似地理标签的起点。

参考

「AI秘籍」系列课程：

  1. 茶桁的公开文章代码库：https://github.com/hivandu/public_articles↩︎

  2. Cory Maklin (2019), Mixture Models Clustering Algorithm Explained (2019), https://towardsdatascience.com/gaussian-mixture-models-d13a5e915c8e↩︎

  3. Ribhu Nirek, Gaussian Mixture Models (2020), https://towardsdatascience.com/gaussian-mixture-models-gmm-6e95cbc38e6e↩︎

  4. Yelp, Yelp open dataset (2019), https://www.yelp.com/dataset↩︎

  5. Vincenzo Lavorini, Gaussian Mixture Model clustering: how to select the number of components (2018), https://towardsdatascience.com/gaussian-mixture-model-clusterization-how-to-select-the-number-of-components-clusters-553bef45f6e4↩︎

使用高斯混合模型识别餐厅热点

https://hivan.me/使用高斯混合模型识别餐厅热点/

作者

Hivan Du

发布于

2024-07-02

更新于

2024-07-16

许可协议

#

喜欢这篇文章？打赏一下作者吧

评论

关注我

链接

分类

最新文章

×