22. BI - 详细来说说 SVD 矩阵分解的三种算法

本文为 「茶桁的 AI 秘籍 - BI 篇 第 22 篇」

[TOC]

Hi, 你好。我是茶桁。

咱们用了两节课的时间来给大家讲解 SVD 矩阵分解原理，并做了一个 SVD 的案例，对一张图片进行压缩。咱们的课程并不是教授算法的，还是的用于 BI，也就是推荐系统。

今天这节课，咱们来看看 SVD 在推荐系统中的具体应用，然后给大家讲解一下三种 SVD 算法：FunkSVD, BiasSVD 以及 SVD++，并展示一个实际的 SVD 推荐系统的案例。最后咱们来说说 Colab 的必要性，如何在 Colab 中加载 Github 和 Kaggle 的数据集。

SVD 在推荐系统中的应用

SVD 用于推荐系统怎么做呢？在推荐系统里面它也是研究矩阵，这个矩阵就是用户和商品之间的评分问题了, 将其转化为 SVD 矩阵分解。

\[ A = U \times \sum \times V^T \\ A: m \times n \\ U: m \times m \\ \sum: m \times n \\ V^T: n \times n \]

把这样的一个矩阵要拆成三块，拆成三块我们也可以把它做还原。

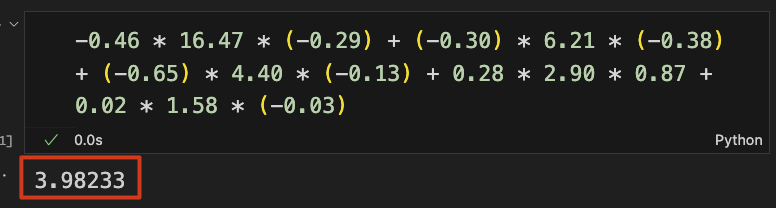
来看看4是怎么来的。4 有几个部分，要进行相乘的，第一部分[-0.46 -0.30 -0.65 0.28 0.02 -0.44] 叫做 user 向量，用户的特征。第二部分对角线就是咱们的 lambda， 最后当然是 item 向量。根据对矩阵的框选就可以看出来，我们是想要看 user2 对 item3 的评分，那依次相乘就可以了，整个等式就变成：-0.46 * 16.47 * (-0.29) + (-0.30) * 6.21 * (-0.38) + (-0.65) * 4.40 * (-0.13) + 0.28 * 2.90 * 0.87 + 0.02 * 1.58 * (-0.03)。

前面我们也讲过了，中间的 S，也就是咱们的 lambda 在对角线上其实从大到小已经排序了，也就说在这个分量上面我们的权重是多少。

把这几个维度相加，最终就得到 3.98233， 对于评分来讲，保留小数点后一位，也就是 4 了。A 中各元素 = user 行向量，item 列向量，奇异值的加权内积。

所以它就是这样的一个拆解的过程。我就可以把一个用户和商品的行为矩阵转化成为一个 SVD 拆解的过程了。

不知道大家在这个过程中有没有发现，其实我们 user 矩阵的最后一列是没有用到的。也就是-0.44这个值，我们没有做任何的计算。

通常啊，就像我们照片很少用原始数据一样，在推荐系统里面因为计算量非常庞大，而且很多数据也不需要那么多的维度，所以我们需要把这个维度给它压缩起来，这样就取少的一些特征。

还以这个简单的数字为例，原来矩阵是多少维度？\(6 * 5\)。就是有 6 个用户和 5 个 item，它们之间的交互现在把它压缩到 k 等于 2，也就是我们的特征个数 = 2.

SVD 在推荐系统里面经常是用于一些降维的处理，所以我们要去取一个小一点的 k 值。那现在 k=2， 我们得到一个近似解 A'。

这里的 2 或者 k 应该小于 min(m, n)，如果它等于的话就不用降维了。通常还不光是小于，我们把它写两个小于号<<， 这个不是书名号啊，这个的含义是表示「远远小于」。

因为在实际的推荐系统过程中用户数和商品数肯定比我们这个例子要大很多很多，有可能是 100 万的用户和 1,000 万的商品。那现在这个 k 一定远远小于 100 万，大概有可能是取 100。那我就直接把用户和商品都用 k 维向量来去做表达了。

用户有 k 个向量维度，商品也有 k 个向量维度，每个向量维度的权重我们都会给它抽取出来。这样信息有没有损失？原来如果是一个超大矩阵，就是 100 万乘上 1,000 万这样一个超大矩阵的话，现在我的信息量只用了 100，所以我的空间是非常小的，还原出来以后肯定还是有损失的。

以刚才这个为例，我们把 k 取成 2 。比如用户里面有这么多的维度，我们只要前面主要的维度，怎么看它主要？是因为 16.47 和 6.21 是它 TOP2 的权重。我们把后面 item 的维度也取成了两个维度。这几个维度做一个相乘，最终还原一下，我们还原出来的结果可以看到它跟原始值是有差距的。就像我们上节课看到我同时的图像一样，还原结果也是有差距的。虽然有差距但是它的差距理论上不会太大。

我们可以看到还是相对比较接近的，1 和 1.41， 5 和 5.18， 0 和 1.27....，总的来说还是接近的，而且他用最少的信息量尽可能的去做了一个近似解。

以上就是在推荐系统里面一个实际的用途，通常我们可以把这个维度做一个压缩用，这个就是 SVD 的概念，就是我们平时大家看到的 SVD。如果你在网上看到 SVD，在招聘里面看到一个技术叫 SVD，它其实指的就是一个降维的处理过程。

我们还是以推荐系统为例，来看一看传统的 SVD 在推荐系统中的应用。 - 我们可以通过 k 来对矩阵降维 \(M_{m\times n} = U_{m\times k} \sum_{k\times k} V_{k \times n} ^T\)。 - 第 i 个用户对第 j 个物品的评分 \(U_i^T \sum_{k\times k} V_j\) - 完整的 SVD，可以将 M 无损的分解为三个矩阵 - 为了简化矩阵分解，我们可以使用 k，远小于 min(m, n)，对矩阵 M 近似还原。

其实在推荐系统里面会存在一些问题，因为最原始的 SVD 是把一个矩阵 A 拆成了 P、S、Q，这里的原始的矩阵是一个无损压缩。而通常我们的 SVD 不会把它用于无损压缩，就像上一节课我们看到的图像一样，SVD 不可能把它拆完以后，拆成了 2,160 个维度又还原出来，那是没有意义的，我们只是把它拆出来 500 个维度。所以 SVD 一般容易降维。

那么 SVD 之所以先做无损是因为方便你做排序找到最大的特征，找到以后求 top-k，这一步就是直接的降维的处理了。所以一般 SVD 是要取前 k 个最大的特征的，这样我们就对原来的矩阵去做了一个还原。这是 SVD 通常使用的一个概念。

还有 SVD 在做矩阵分解的时候其实也有一个情况，就是我们希望矩阵是一个稠密矩阵。那之前给大家讲过稠密的概念了，就是说我们应该没有缺失值，或者说缺失值其实并不多。但我们想一想，在推荐系统里面矩阵通常是怎样的情况？是稠密的还是稀疏的？在推荐系统里面，我们以电影推荐场景为例，100 万的用户面对 10 万的电影他们的评分矩阵可能是稠密的吗？通常我们的用户行为绝大部分应该是怎样的？肯定是稀疏的，通常情况下一定是稀疏的，而且是非常非常稀疏，经验告诉我们大体上是 1%，99%的情况都是用户没有发生行为的。

那 SVD 之前要求是稠密的才能做无损压缩，现在怎么办？这里我们就不能做无损压缩，而是要去把它做一个降维的处理，把它压缩一下。压缩以后就变稠密了，原来的向量空间是很多的，现在我们把它压缩一下压到一起，就像很多空气一样，你把它压实了。这样就变成一个稠密的小矩阵了，稠密的小矩阵在还原以后就变成了一个稠密的还原矩阵。

也就是说原来是 1%的训练的数据，我们就可以还原预测出来 99%的数据。这个就是 SVD 的价值，有点像我们的 ALS，之前给大家讲的这个过程，所以它其实跟我们的 ALS 的原理是一样的。

FunkSVD 算法

我们在这里给大家看一个算法，叫做 FunkSVD，FunkSVD 就是最早基于 SVD 去做推荐系统的一个算法。它是需要我们先设一个 k 值，来对矩阵近似求解。

矩阵补全以后，再预测，实际上噪音大。矩阵分解之后的还原，只需要关注与原来矩阵中有值的位置进行对比即可，不需要对所有元素进行对比。

\[ M_{m\times n} \approx P_{m \times k} ^T Q_{k\times n} \]

我们来看，之前咱们在等号后面设置的是 P、S、Q，对于任何的矩阵可以拆成 3 个小矩阵。那现在我们的 S 跑哪里去了？这个 S 是一个对角线的向量，其实它本身严格上来讲不属于一个矩阵，可以把一个 S 拆成两边，分别代入到 P 和 Q 里去。

那其实我们有两种代入方式，一种是 S 分为 lambda_1 和 lambda_2，开根号之后分别代入到 P 和 Q 里去，还有一种方法是只代入到一边，代入到 P 或者 Q 里，所以通常我们最终写完的这个方式跟之前看的矩阵是一样的。也就说我们不把一个大矩阵拆成 3 个了，就直接干脆把一个大矩阵拆成两个，拆成 P 和 Q。这个就是之前讲的那个最终结论，一个大矩阵拆成两个矩阵的最终状态。有了这个状态以后你就可以去构造一个方程。

现在的方程其实跟之前课程中的应该也有点类似，我们想要去构造一个预测，让我们的预测值和用户的实际评分的差尽量的小，就会写一个损失函数 loss function 的预测值。

看这个预测值该怎么写，用一个 P 和 Q 去做一个乘法，和原来的值去做一个相减

\[ \sum_{i, j}(m_{ij} - q_j^Tp_i)^2 \]

这个函数我们应该很熟悉了，就是 MSE。现在求的是个回归问题，所以就直接用回归问题做一个损失函数，求一个回归值，希望它最小。

除了它以外之前课上给大家说过，一个矩阵里面如果有个 m，这个 m 没有出现过，要不要放到我们的损失函数里来去让它最小化？那这跟我们在上一课中的图像压缩也应该是类似的问题，如果你想要去做一个 loss function，让它跟之前的值做对比的话，你只需要做哪一个部分？只需要把原来已知的给它做一个计算就好了，没有的值就不要计算，因为你无法知道它真正的值差在哪里。

\[ argmin_{p_iq_j}\sum_{(i, j) \in k}(m_{ij} - q_j^Tp_i)^2 + \lambda(||p_i||_2^2 + ||q_j||_2^2) \]

后面我们为了防止过拟合，增加正则化项，它的目的就是约束你的 P、Q，让我们的参数尽量的小。因为它也是个代价，所以要把整体做一个优化处理。

是不是觉得和我们之前讲的课程内容非常像了？其实 FunkSVD 在前面的过程，推导结论是一样的。区别就是优化算法。之前课程给大家讲的 ALS 本质是优化方法，这个方法是固定一个求解另一个。除了这种方法以外在求解以上的机器学习的目标函数还有什么？机器学习里面最通用的优化策略就是随机梯度下降，FunkSVD 就是利用了梯度下降法，让我们的 P 和 Q 参数最小化。所以梯度下降是机器学习里面比较常见的方法。

通过不断的参数的优化，P 和 Q 就给它补全了，只要 P 和 Q 进行补全，最终我们就可以把原来的矩阵给它预测出来，这样就可以把缺失的值找好，找好以后按照从大到小的方式来进行推荐。以上就是推荐系统在 SVD 的这个方法下的主要原理。区别就是一个梯度下降的概念，从目前来看好像跟 ALS 的差别还不是很大。

BiasSVD

除了 FunkSVD 优化方法以外，作者还又写了一个新的算法，他做了一些改进，提出来一种叫做 BiasSVD 的方式。BiasSVD 认为用户有自己的偏好(bias)，商品也有自己的偏好(bias)。

举个例子，乐观的用户就喜欢打高分，他可能经常打高分，我们就把它称为叫乐观用户。商品是不是也有好坏之分呢？质量好的商品成绩一般也比较高。这两个部分把它单独拆出来，我们认为它不是个性化的。什么叫个性化，就是专属于这个用户的情况叫个性化，上面这个还是一个相对通用的策略了。

一个用户乐观，那么他对所有人都乐观。一个商品好，那么所有人都会认为它好。这些我们把它拆出来，剩下的部分，也就是用户和商品之间就是一个偏好个性化的部分。因此我们可以把打分拆成两块儿组成，mu 加 bi 加 bj： \(b_{ij} = \mu + b_i + b_j\)，mu: 所有记录的整体平均数，bi: 用户偏好（自身属性，与商品无关），bj: 商品偏好（自身属性，与用户无关）。

是不是有点像我们之前课程中给大家介绍的那个方法，在 surprise 里面一个叫 baselineOnly 的方法，大家有回忆起来吗？（17. 详解 Surprise 工具箱中的 Baseline）不过今天这个方法不等于 baselineOnly，因为它后面还加了一个个性化的参数(\(q_j^Tp_i\))。

我们的模型不是只有 bi 和 bj，用户和商品编号，还有一个个性化的成分，这个 q 和 p 怎么来的？就是拆出来的，可以一起来看一看。

我们的目标函数里面，如果把 bi 和 bj 也当成一个参数，那方程里面有几种参数？就是你的参数的维度有几个？以前是两个维度 p 和 q，所以可以用固定一个求解另一个，把 p 固定求 q，或者把 q 固定求 p。现在加上了 BiasSVD，加用户偏好的这种方法，我们要学习的内容参数量的种类有 P，Q， bi 和 bj，四种。mu 代表的是系统的平均值，所以这个参数是固定的，这个参数是第一次就可以计算出来，它不需要猜。那么 mu 就不需要学习了，把 mu 去掉以后要学习的就是四种。

四种我们也可以做正则化项，大家记住，正则化项是要对你模型里面所有的参数去求一个乘法，如果你希望 P、Q 还有 bi, bj 都要比较小，那你可以把它都放到正则化项里面。正则化项有两种，L1 和 L2，这里应该比较明显是 L2。

\[ argmin_{p_iq_j}\sum_{(i, j) \in k}(m_{ij} -\mu - b_i - b_j - q_j^Tp_i)^2 + \lambda(||p_i||_2^2 + ||q_j||_2^2 + ||b_i||^2_2 + ||b_j||_2^2) \]

除了 L2 以外能不能用 L2 呢？也可以的，不同的 BiasSVD 里是可以自己去做设置的，可以用一阶，相对来说二阶可能收敛起来速度会更快。

以上就是一个相对复杂的模型，我们在原来的 P、Q 的基础上又加了 bi 和 bj，就是用户的特征和商品本身的特征，有 4 个参数需要进行学习。

在 4 个参数进行学习过程中，用 ALS 还好用吗？或者说还能用 ALS 吗？ 之前我们讲过，ALS 就是固定一个求解另一个，那现在怎么固定？可能要固定 3 个求解一个，再固定 3 个求解一个。这种方法的是不是显得就比较麻烦了。所以干脆我们就直接用 SGD，也就是不采用固定一个求解另一个，就批量的同时来进行学习。

在迭代过程中，bi，bj 的初始值可以设置为 0 向量，然后进行迭代：

\[ b_i = b_i + \alpha(m_{ij} - \mu - b_i - b_j - q_j^Tp_i + \lambda b_i) \\ b_j = b_j + \alpha(m_{ij} - \mu - b_i - b_j - q_j^Tp_i + \lambda b_j) \\ \]

机器学习里面参数量很多，维度也很大。SGD 就比较百搭，它可以对很多的维度一起来做处理，这就是 BiasSVD。所以在我们的 surprise 里面你看到的 SVD，它都是基于 SGD 这样的一种特性来去完成的。

SVD++算法

BiasSVD 的原理以上就简单讲解了一下，除此之外，作者后来又提出来一种新的方法，就是 SVD++，称之为 SVD plus plus。

它的改进是加入一种隐式特征，如果说以前用户的评分叫显式，那隐式我们考量的是什么样的用户行为？之前课程中对隐式和显式行为有过讲述，还记得是哪一种用户行为吗？

推荐系统里面除了显性的表达以外其实有大量的信息是用户的隐含的表达，比如说以哪一些特征为例呢？点击的信息、浏览的信息，这些信息能直接判断用户的倾向或者喜好吗？代表用户是喜欢还是不喜欢。显然不能，虽然不能但是这个数据量很大，它可以间接的反应。我们也在推荐系统里考量到这样的一些特征，就要用到 SVD++ 这个方法。

对于某一个用户 i，假设他的隐式反馈 item 集合为 I(i)， 用户 i 对商品 j 对应的隐式反馈修正值为 cij, 用户 i 所有的隐式反馈修正值之和为\(\sum_{s\in N(i)}c_{sj}\)，除以 ||I(i)|| 的平方根，可以消除不同个数引起的差异。

SVD++ 会考量隐式的一些特征，帮你去做一些目标优化。我们在目标优化过程中又加上了一个维度，所以它一共有五个维度，这五个维度都同时来去做正则化项，得到 P 和 Q。

\[ argmin_{p_iq_j}\sum_{(i,j) \in K} \begin{bmatrix} m_{ij} - \mu - b_i - b_j - q_j^Tp_i - q_j^T|I(i)|^{-\frac{1}{2}}\sum_{s\in I(i)} y_s \end{bmatrix}^2 + \lambda \begin{bmatrix} ||p_i||_2^2 + ||q_j||^2_2 + ||b_i||_2^2 + ||b_j||_2^2 + \sum_{s \in I(i)}||y_s||^2 \end{bmatrix} \]

以上就大概把 SVD 这个推荐系统里的原理给大家讲完了。

SVD 算法工具

我们梳理一下，讲了三种算法，第一个叫 FunkSVD，它的特点是只有 P 和 Q，其实跟 ALS 是一样的，只不过用了 SGD 的方式做了学习。这样我就把一个大矩阵拆成两个矩阵。再下一个进阶的方式叫 BiasSVD，不光有 P 和 Q 了，还有 bi 和 bj，同样采用 SGD 的方式来进行学习。再之后我们讲了 SVD++，在原来基础上又加了一个隐式的方法。

这三个方式都是 SVD 家族，调包就可以在 surprise 这个工具箱里进行调包。surprise 工具箱如果你不知道该怎么去调，可以直接找到 surprise 的帮助手册，https://surprise.readthedocs.io/en/stable/。之前在如何读论文那篇文章中（19. 学习人工智能如何从阅读论文中获取一手信息，并推荐一些技术论文）我也有讲到这个手册。这个帮助手册里面写的是非常的详细，大家可以看一下。

我可以搜索一下 surprise，在 surprise 这个文档里面的话你想去做哪一个操作，比如说 SVD，可以搜一下。

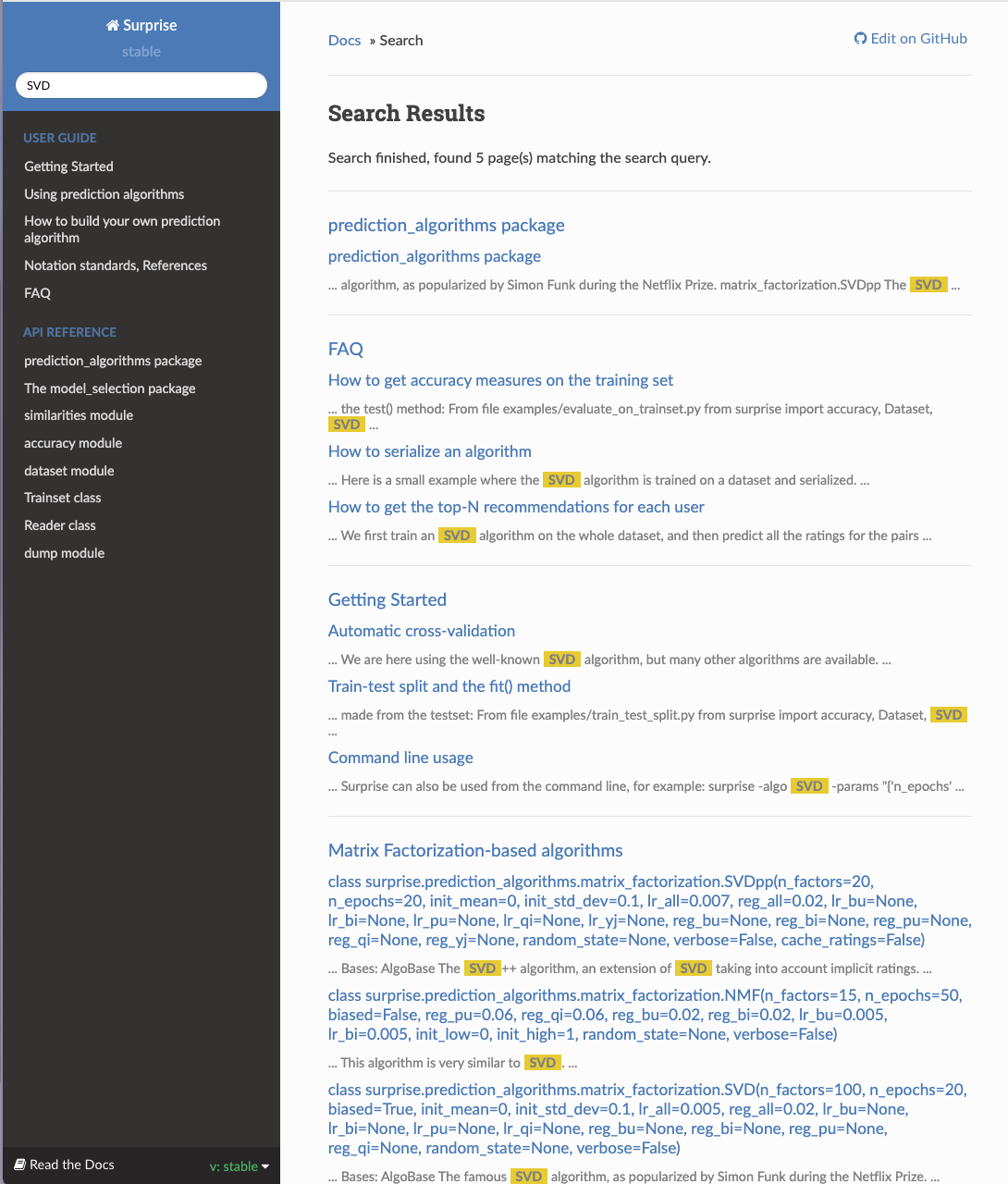
它上面会提供一些 SVD 的方法，我们把它打开可以看看。它有两个包，都在哪个包的前缀呢？叫matrix_factorization，中文叫做矩阵分解，矩阵分解里面的 SVD。

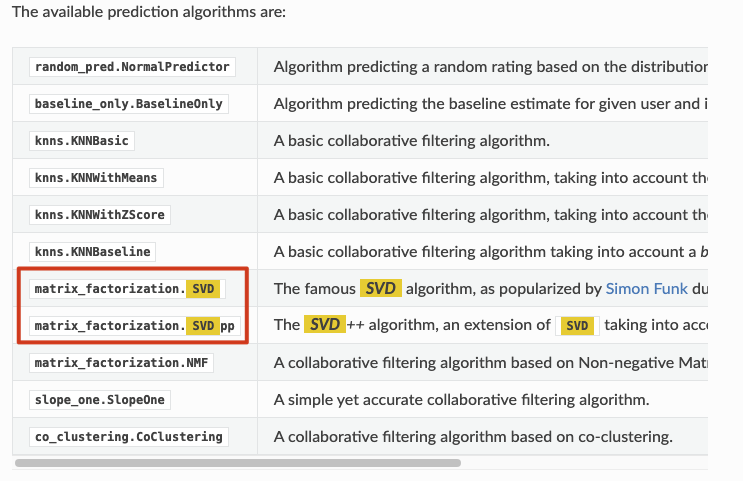
SVD 是由 Simon Funk 这个人创建的，因此我们也把它称为叫做 FunkSVD。点进这个包，可以看到一个详细的介绍。

那咱们一共学了三种 SVD 算法，BiasSVD 跑哪去了？Bias 是作为一个参数了。

它告诉我们是使用基础的版本还是使用 BiasSVD 的版本，默认情况下为 true，也就是说默认情况下是带 BiasSVD 的。如果想要用 FunkSVD 可以将参数值设成 False。

所以，默认调包 SVD 直接是 BiasSVD，关于它的论文在链接里面是可以看到的，感兴趣同学可以连接过去看一看，也就是今天给大家讲解的这套原理。

BiasSVD 算法有一些参数量可以进行设置，比较常见的参数如下：

• n_factors: k 值，默认为 100
• n_epochs: 迭代次数，默认为 20
• biased: 是否使用 biasSVD，默认为 True
• verbose: 输出当前 epoch，默认为 False
• reg_all: 所有正则化项的统一参数，默认为 0.02
• reg_bu: bu 的正则化参数
• reg_bi: bi 的正则化参数
• reg_pu: pu 的正则化参数
• reg_qi: qi 的正则化参数

k 就是把向量进行压缩，取它前 k 个主要的成分。k 默认等于 100，这样我们的维度不会失去太多的精度，100 维基本上可以取出来比较重要的一些特征了。

如果是 biasSVD 就会有 4 个正则化的参数了，有 bi 和 bu 的部分，还有 p 和 q 的部分。如果你觉得比较麻烦可以设置一个 reg_all，这四个参数都等于一个值，默认是 0.02。

以上这些就是 BiasSVD 里面最常见的一些参数的配置，把这些参数配置设置完成以后就可以来进行预测。

对比之下 FunkSVD 这个鼻祖如果你要调包的话只要改一点，就是把 BiasSVD 设为 False，我们就不会预测 bi 和 bj 的部分了。

k 值代表的是它的颗粒度，如果你希望做的稍微精细一点，k 就稍微大一点。

SVD++ 这种方式是隐式的分类，它的数量级往往会非常庞大，所以你可以从参数配置上面找到 k 值，默认为 20。如果它数据量级非常庞大，k 就不能太精细，如果太精细计算量就会非常多。这里的 k 默认等于 20，迭代次数跟之前的方法一样，默认也是 20 次。这样我们就可以有 5 个需要学习的参数，所以除了之前要设置的四个正则化参数之外，还有一个 reg_yj: yj 的正则化参数。

这就是三个工具箱，你可以自己去体验一下。我们还是以 MovieLens 电影推荐系统为例，一个非常经典的网站，在这个网站里面我们有四个字段，怎么样去使用它？

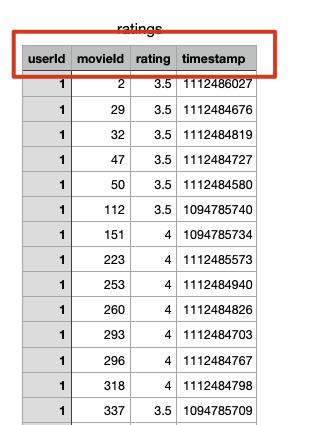
这四个字段就是用户在某一个时刻对电影的一个打分，如果要去使用它首先我们要确定是不是用户和商品之间的行为，如果是用户和商品之间的行为可以想到矩阵分解，想到 SVD。如果你用 FunkSVD 应该把 biasd 改成 False。

来看看代码，跑一遍看看。

首先还是要进行数据读取，这个和之前我们讲 surprise 的时候一样，

# 数据读取
reader = Reader(line_format='user item rating timestamp', sep=',', skip_lines=1)
data = Dataset.load_from_file('dataset/movies/ratings.csv', reader=reader)
train_set = data.build_full_trainset()

然后我们需要将模型设置为 SVD

# 使用 funkSVD
algo = SVD(biased=False)

我将 biased 设置为 False 了，那就是说我们这次用的是 FunkSVD。

然后定义一个 k 折验证，k=3，然后把每一轮的结果打印出来，求解它的 RMSE。

# 定义 k 折交叉验证迭代器，k=3
kf = KFold(n_splits=3)
for trainset, testset in kf.split(data):
    # 训练并预测
    algo.fit(trainset)
    predictions = algo.test(testset)
    # print(preictions)
    # 计算 RMSE
    accuracy.rmse(predictions, verbose=True)

---
RMSE: 0.8736
RMSE: 0.8716
RMSE: 0.8727

fit 以后, 最后 predict 预测我们的用户和商品之间的交互行为。还是来看 196 用户对 302 这个商品的打分会是多少分，参考值还是 4。

# 输出 uid 对 iid 的预测结果
pred = algo.predict(uid, iid, r_ui=4, verbose=True)

---
user: 196        item: 302        r_ui = 4.00   est = 3.97   {'was_impossible': False}

最终的结果相对还好, 也有一定的科学原理。最后得出来差不多不到 4，相差不大。

Colab

以上就是咱们 SVD 工具算法的讲解以及实现。最后实现的时候我们会发现可能每一次运行的时间还是会有点长，协同过滤如果你要把矩阵放进去它的运算时间，运算的量还是比较大。那该怎么办呢？

不知道大家以前有没有用过 Colab 或者类似的一些工具。这里就给大家介绍一个云端的 Jupyter 的工具，使用起来还是非常方便的。

你想要去更快的去跑你的程序，或者在后面我会给大家看一个深度学习就可能会用到一个 DeepFM 的工具，这个工具就可能要在 Colab 上去跑。建议大家还是去用一下 Colab。Colab 是 Google 出品，是一个云端的 Jupyter，计算效率还是非常快的。

要去执行 Colab，我们需要挂载一下自己的 Google Drive，关于如何去使用，我意思是如何去访问，这里就不提供方法了，大家还需要自己去弄一下。

from google.colab import drive
drive.mount('/content/drive')

需要注意一点，最好是下载一个 Google Drive 的本地客户端，直接从网页上传有可能将 csv 转成 gsheet，这是 Google 表格的格式，这个数据是不好去读取的。

和在本地一样，在 Colab 上去执行，需要安装环境：

!pip install surprise
!pip install pandas

Colab 是默认保存 12 个小时的环境，12 小时过后会清理重置，不过也是足够了。

以上代码我也做了一个实验，分别在我的 M1 和 Colab 上执行了一下，前后加了一个 time 来进行计算，那我们打印之后我发现，我的 M1 还是蛮快的，至少在这段代码的执行效果上，居然是高过了 Colab 的 TPU 模式

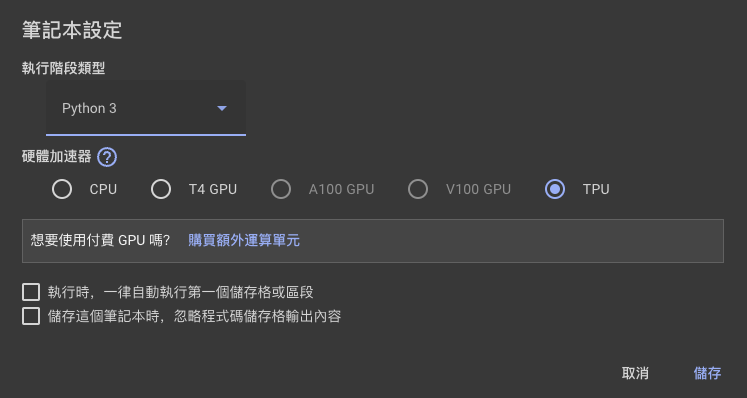
我在 M1 本地的执行效果：

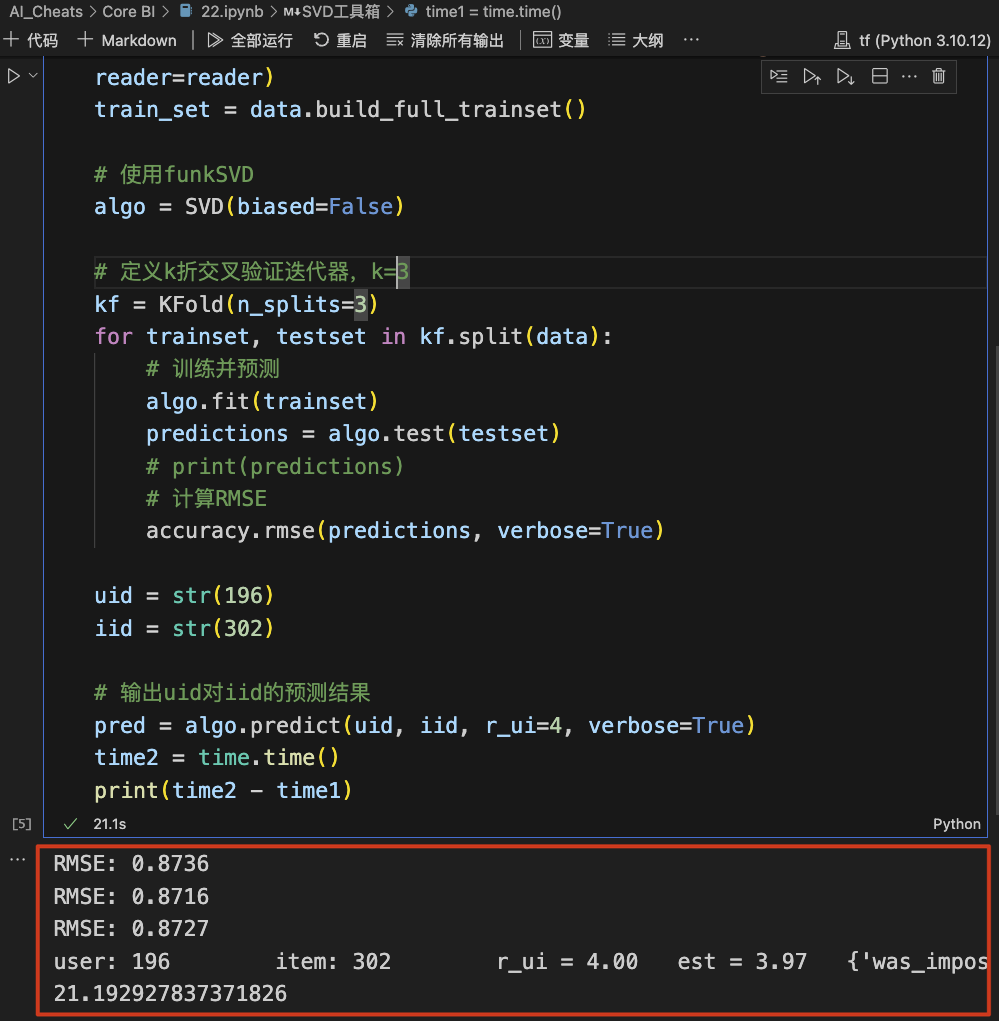
在 Colab 上的执行效果：

分别是 21.2 秒和 87.4 秒，这个倒是真的超出我的预计了。不过之后咱们在使用 DeepFM 的情况下，最好还是用 Colab 的好，毕竟自己电脑上的 GPU 还是不如 Google 提供的，更何况，如果你和我一样是 M1 电脑的话，可能大部分是不支持 GPU 运算的，只有部分框架支持了 M1 的 GPU（mps）。

这里多提一句，M1 是平果自主研发的芯片，目前已经发布到 M3 系列了，这是一款混合型的芯片（SoC）， 集成了 CPU，GPU 和 NPU 等多个处理器。所谓 NPU，就是神经网络引擎。但是目前为止，大部分框架对其支持并不好，当然，主流的 PyTorch 和 Tensorflow 都有做对其支持。

不管如何，我还是建议大家能用 GPU 就用 GPU，没有 GPU 的还是用 Colab。真实的差距还是蛮大的，平均可以差到 20 倍左右。不过平果的 M 系列芯片还真是超出我的预计了，我也没想到它的表现会如此好，鉴于现在越来越多的框架开始支持 M 芯片的 GPU，有兴趣的也可以去搞一个，条件允许的话，最好是搞一个 32G 以上的 M3 系列，据说 M3 系列的 GPU 表现上还是非常不错的。

除了 Colab 之外，阿里和百度也有自己的在线 Jupyter。百度的飞桨有一个小的问题，就是它不能去加载谷歌的 Tensorflow 或者是 Facebook 的 Pytorch。

Kaggle 也有自己 Notebook，这些都可以去选。Kaggle 是被 Google 收购了，如果用 Colab 直接加载数据集的话，Github 和 Kaggle 都还是比较方便的。

如果要使用 Github 数据集，直接用 git clone 就可以了：

!git clone https://github.com/xxxx/dataset.git
!pip install git+https://github.com/shenweichen/DeepCTR.git

如果是 Kaggle 数据集，那要先生成一个 Kaggle API，然后找到自己的 username 和 token，创建 Kaggle 文件夹，配置 kaggle.json，然后使用 kaggle api 下载数据集，最后解压数据并使用。

# 安装 kaggle
!pip install -U -q kaggle
# 创建 kaggle json
!mkdir -p ~/.kaggle
!echo '{"username":"hivandu", "key":"xxxxxxx23456789ftyghujiklocvbnm"}' > ~/.kaggle/kaggle.json
!chmod 600 ~/.kaggle/kaggle.json

# 设置数据集文件夹
!mkdir -p credit_data

# 下载数据
!kaggle datasets download -d uciml/default-of-credit-card-clients-dataset -p dataset/credit_data

# 解压数据
!unzip /dataset/credit_data/default-of-credit-card-clients-dataset.zip

在后面的训练过程中如果用到了深度学习，你要选一个能用的平台，这样才能把 GPU 挂载进去。

好，SVD 这几节课咱们就基本讲完了。在原理上我们主要讲解的是奇异值分解 SVD，它的本质是对一个大矩阵拆成三个小矩阵，实际工作中是要抽取前 k 个特征的。这里的 k 相当于是对矩阵的一个降维，通过之前我同时那个照片的抽取可以看到，10%的特征是可以包含 90%以上的信息，这就是 SVD 的一个价值。

在推荐系统里面我们确实也需要进行降维的处理，因为原来太稀疏了，降维以后才能变得稠密。在 surprise 这个工具箱里面有三种工具，就是今天给大家看的三种工具。最后也跟大家说了，MF（矩阵分解）虽然是推荐系统底层使用的工具，但它现在并不直接来进行使用。直接来进行使用可能是要采用另一个工具，叫因子分解机（FM），因为它有更好的泛化能力，有时候它可以对接更多的特征来放到模型里面一起来去做训练。

基本上咱们近期所讲的这些内容都是协同过滤的思想去完成的。surprise 这些工具箱之后大家还是要多去做一些练习，针对我场景来去完成。

那今天的课程就到这里，咱们下节课开始要讲解基于内容的推荐了。