25. BI - 带你详细了解十大经典机器学习模型之 Google 的基石：PageRank

本文为 「茶桁的 AI 秘籍 - BI 篇 第 25 篇」

[TOC]

Hi，你好。我是茶桁。

我们今天要学习的内容是 PageRank，很多同学应该对这个不陌生。这个是 Google 最初推出的，十大经典机器学习之一。

在之后咱们还要来看看一些图论的方法。图论的使用场景非常多，在推荐系统里面也会使用到图论。我们来一起看一看怎么样在图中表示用户的信息，商品的信息，可以把它看成一张图。那我们就要来看看图论和推荐系统他们之间的一些关系。

什么是 PageRank

Google 是非常有名的搜索引擎，在 Google 之前有没有其他的公司在做搜索引擎？大家知道谷歌是在 1998 年成立的，在 1998 年之前还有一家公司也是做搜索引擎，就是 Yahoo，它已经做出来了搜索引擎。那为什么后来又被谷歌反超了呢？因为在雅虎的搜索过程中人们发现搜索的质量并不高，而且容易作弊。

怎么样来去作弊？作弊就是换取一些流量，本身跟你的页面搜索的内容不相关，但是你通过一些运作的方式可以把你的页面顶到上面去，这样就会产生一些误导。

比如用户想要搜「口罩」这个内容，怎么样排到前面去？其实就是要看搜索引擎的原理。搜索引擎一定是要跟这个关键词匹配，如果它匹配了就证明你的页面会跟它相关。那么我们可以用一些优化的方法，即使你的页面跟口罩没有关系，我也把关键词放进去，这样就会形成大量的关键词的堆砌。

假设一个用户搜索口罩，但这个页页面又跟口罩没有任何的关系也会被搜索出来，这样对于用户来说这个页面可能就并不是他想找的内容，商家可以为了得到更多的流量而产生一些作弊的行为。

Google 发现了这个问题，就想有没有一种算法可以让优质的页面呈现到前面去。那么我们的算法就需要有两个维度，第一个还是要匹配内容，用户检索口罩这个关键词，你的内容也要出现这个内容，这是一个充分条件。还有一个条件，我们想要对所有符合的这些网页做一个排序，按照权重排序，Rank 就代表的是排序的含义。

符合口罩这样的关键词的页面可能会有上千万个页面，怎么样来去做排序就是 PageRank 这个算法来去产生的。

最早这两个人也是在 Stanford 读计算机的博士，一个是拉里佩奇，还有他的同学。他们两个也是基于这个方法创建了谷歌公司，对海量的网页重要性来做了一个排名，通过这个方法用户可以找到更有质量的一些页面。他们的搜索引擎就可以帮助人们找到匹配的内容。

这个 PageRank 的模型是怎么产生的？之前咱们有过课程来讲解如何看论文，那论文里哪些指数会证明一篇论文的影响力比较高？如果你写过论文会发现在论文里面有一个部分可以对你论文的影响力来做个衡量。我们需要找一个指数，这个指数就跟论文的影响力成一个正比，就是引入率。

如果别人都引入你的论文，有上百个引入次数，那就证明你的影响力很高。那在大学里，如果你要申请院士，有一个不成文的一个规定就是你在某一个领域过程中至少要有一篇影响力大于 500 次，也就证明你是这个领域里面的权威，就变成了一个门槛。

所以论文的影响力按照引用次数，拉里佩奇把它当成了一个核心的指标。并且我们知道论文的引用关系就像一张图一样，它还不光是一个简简单单去做了一个次数的排名，过程中会有一些先后的关系，所以是在图论过程中做了一个 rank，做了一个排序。

图论基本知识

关于图论，我在「数学篇」中有写过专门讲解图论的文章，大家有兴趣的可以去看看，包括： - 23. 图论 - 图的由来和构成 - 24. 图论 - 图的表示&种类 - 25. 图论 - 路径和算法 - 26. 图论 - 树

咱们这里讲到图论，要先对图论的基本知识有一个概念。我们有两种图，一个叫有向图，还有叫做无向图。

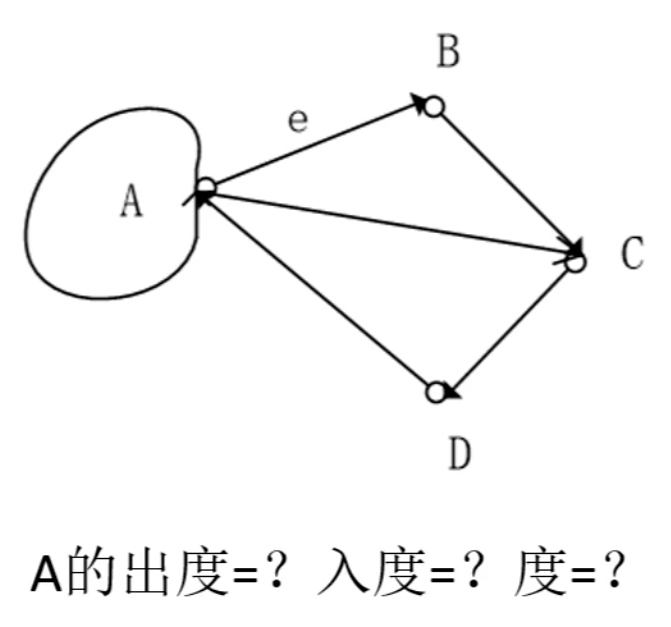
什么是有向图，我们来看这张图。有向图就是边有方向的图，也就是 A->B != B->A。有向图的就是一个单行线，或者说从 A 走到 B 和从 B 走到 A 实际上是不一样的，这两个是两条边。

那无向图呢，对于无向图来说你可以把它认为是 A 到 B 和 B 到 A 都是一样的，它没有方向。

以上就是有向图和无向图的概念。除此之外，还有两个概念：出度和入度。

入度是什么？有向图中，我现在是一个顶点 A，那有多少个其他的顶点指向我，也就是以我作为终点，这个次数和就是入度。

出度则刚好相反，同样是有向图中，我现在是一个顶点 A，我指向了多少个其他的顶点，也就是我作为起点，这个次数和就是出度。

那度就是出度+入度，称之为节点的度。

那这张图中，我们计算一下，A 的出度等于多少，入度等于多少，度是多少？

我们先看它的出度，出度就是从 A 指出去的，A 到 B 是一个，A 到 C 是一个，我们还注意到 A 本身有一个环，如果存在了一个环形那么它就既有出度又有入度。先从出度上去看应该算是 2+1=3 条边，入度应该是两个，度就是 3+2=5。

所以我们去衡量 A 和其他顶点之间的一个频次，它的一个关系，就可以通过出度入度和度来进行计算。

PageRank 简化模型

接下来咱们来理解一下链。链就是边的含义，出链就是链接出去的一个边，入链就是收到的一条边，也就是 链接出去 的链接 和 链接进来 的链接。那我们来思考这个问题：一个网页的影响力怎么去评估它？

要说影响力，那肯定是计算别人引入我，那要计算的应该就是所有入链的集合。他们把影响力投票给了你，你把这个投票的票数做一个累加，也就是所有入链集合的页面的加权影响力之和。

\[ PR(u) = \sum_{v \in B_u} \frac{PR(v)}{L(v)} \]

U 是你要计算的影响力,v 就是你的入链的边的集合。他们会给你来做投票，所以上面是一个累加的符号。下面又除以了一个部分，为什么要除，因为他投票给我同时又不仅仅投给我一个人，投给了多个人。如果他投了三个人我们就用 \(PR(v)\)除上 3，如果投了两个人就除上 2，如果是投给三个人，那么我的投票就是他的 1/3。

那 1/3 这是一个点，所有的点加到一起，看看这个人投了几个人，我们就会被分流，最后做一个累加，就等于我的影响力的一个计算。

所以从公式上面来看，你去把你的邻居都找到，这里的邻居是你的入链的集合。然后每一个 v，它的链接出去的边的个数我们用 \(L(v)\)来做一个表达，这样我们把这些所有的和做个累加，就等于我自己的一个影响力。

我们来总结一下，u 是待评估的页面，\(B_u\) 是 u 的入链集合。

对于 \(B_u\) 中的任意页面 v，它能给 u 带来的影响力是其自身的影响力 \(PR(v)\)除以 v 页面的出链数量。即页面 v 把影响力 \(PR(v)\)平均分配给了它的出链。这样统计所有能给 u 带来链接的页面 v，得到的总和即为 u 的影响力，即为 \(PR(u)\)。

我们举一个例子，我们来看这个图：

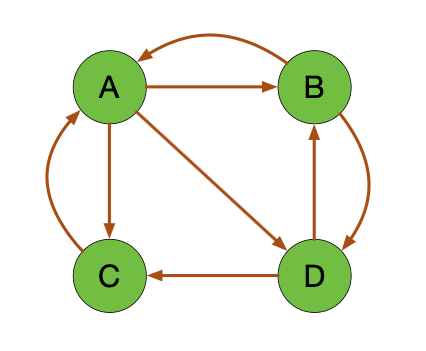
比如说 A 的影响力该怎么去进行计算？首先来看，是谁给了 A 影响力？应该有两个部分对吧，一个是 B，还有 C，那就是 \[ PR(A) = \frac{PR(B)}{2} + \frac{PR(C)}{1} \]

A 的影响力 \(PR(A)\) 应该是它的两个入链 B 和 C 的影响力的和，那 B 将自己的影响力给了两个，一个 A，一个 B，所以除以 2. C 则只给到了 A，所以除以 1。

所以对于$ PR(A)$，实际上就是由 B 和 C 来去完成的。看一看它们链接出去多少条边来做一个加权的一个平均。

以上，咱们就把影响力的计算公式做了一个说明。所以我们要去衡量影响力，这是一个关键指标。

从刚才的影响力的一个跳转过程中，我们可以把它梳理出来，就相当于最开始我把它分成 10 票，每个人都有 10 票。初始的影响力，可以假设这四个人都是一致的，都等于 10 或都等于 1，但是通过分配的原则你把你的票数分给了你出链的这个边，那他的影响力就会发生变化，下一次影响力就变了。再下一次他可能也会变，怎么变，我们就用一个转移矩阵指明了他如何来去分配你的影响力。

转移矩阵，就是统计网页对于其他网页的跳转概率。

我们再来一起看看这张图

一起看一看, 有几个顶点呢? A、B、C、D，将四个顶点矩阵化，行上分别是 A、B、C、D， 列上也依次是 A、B、C、D

\[ M = \begin{bmatrix} 0 & 1/2 & 1 & 0 \\ 1/3 & 0 & 0 & 1/2 \\ 1/3 & 0 & 0 & 1/2 \\ 1/3 & 1/2 & 0 & 0 \end{bmatrix} \]

我们在转移过程中 A 到 A 下一次是没有的，所以它为 0。那 A 的出链都有哪些？B、C、D，所以它能走出三条边出来，其影响力分配就是针对 B、C、D，各分配 1/3。

同样我们去看 B，B 的出链是 A 和 D，那它下一次它就会走到 A 和 D，所以影响力分配是 A、D 各分配 1/2，B 没有到 C 的出链，所以也为 0，自己到自己也为 0。

然后看 C，C 下一步只走到了 A，所以就是百分百给到了 A。

然后是 D，D 包含出链到 C 和 B，所以它 1/2 分别给了 B 和 C。

这里就是用到了 \(L(v)\)的概念，你出去几条边就相当于是被分配了几次，就除上 \(L(v)\)。因此我们这里的转移矩阵就表明了会如何把现在的影响力分配给相应的邻居。

有了这个转移矩阵我们就可以去模拟影响力的变化。我们先假设一下，A、B、C、D 最开始的影响力都是相等的，我们又认为A+B+C+D=1，那么这几个都相等，我们就假设 A、B、C、D 都等于 1/4，1/4 是初始的状态。

\[ w_0 = \begin{bmatrix} 1/4 \\ 1/4 \\ 1/4 \\ 1/4 \end{bmatrix} \]

一次转移之后，我们就针对这个状态去乘上了一个转移矩阵，就等于他下一时刻的状态。

\[ w_1 = Mw_0 = \begin{bmatrix} 0 & 1/2 & 1 & 0 \\ 1/3 & 0 & 0 & 1/2 \\ 1/3 & 0 & 0 & 1/2 \\ 1/3 & 1/2 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1/4 \\ 1/4 \\ 1/4 \\ 1/4 \end{bmatrix} = \begin{bmatrix} 9/24 \\ 5/24 \\ 5/24 \\ 5/24 \end{bmatrix} \]

为什么是这样的一个结果，我们还是以 A 的下一时刻为例一起来看一看。A 的下一时刻是由 B 和 C 组成的，\(PR(A)\)的下一时刻应该等于 \[ \frac{PR(B)}{2} + \frac{PR(C)}{1} = \frac{1/4}{2} + 1/4 = 9/24 \]

所以 A 的下一个时刻的影响力就等于这个值。

原来是 w0 第 0 时刻，现在是 w1 第 1 时刻，我们现在想想，再下一时刻还有 w2， 那 w2 怎么算？w2 就是把 w1 放在之前 w0 的位置，再去乘上一个转移矩阵，就变成 w2。那 w3，第三时刻就把 W2 放在原来 w0 的位置，再去乘，不断地乘，你会发现数值会一直发生变化，但是在某一个时刻为止它的数字就不再发生变化了。我们也可以做个模拟,一会可以给大家看一看。

如果第 n 次迭代之后影响力不再发生变化了，那也就意味着你再怎么乘 M 它最终还等于 wn。这样我们的影响力就稳定了，也把它称为页面的影响力收敛。影响力稳定了，就可以得到最终的状态，就是 A、B、C、D 的影响力。

那得到最终的状态之后，这几个影响力相加以后还等于 1。

\[ w_n = \begin{bmatrix} 0.3333 \\ 0.2222 \\ 0.2222 \\ 0.2222 \end{bmatrix} \]

那现在谁的影响力最大？如果按照影响力排名来去看，应该就是 A，其次应该就是 B、C、D，这几个影响力都是相等的。我们就可以知道，A、B、C、D 可以是四篇文章也可以是四个人，他们只要有这样的一个链接的关系，最终影响力就会趋于稳定，就可以知道 A 这篇文章或者 A 这个人在这个网络过程中的权威，他是排名第一的，其次是 B、C、D，他们是并列第二名。

以上咱们就讲了 PageRank 的一个简化版的模型. 拉里佩奇当时读 Stanford 的一个博士论文主要就是刚才提到的这个 PageRank 的方法.

通过 A B C D 这个例子我们就可以去推导出 PageRank 整个计算的过程. 先给他一个初始化的值, 通过转移矩阵去改变每一次的影响力的计算, 通过 n 次的迭代影响力不再发生变化, 就等于最终的状态. 这样我们就可以对 A B C D 四个顶点去做排序, 得出来它的一个排名.

这个原理我们也可以通过程序去做个模拟, 咱们来一起体验一下. 我们有一个模拟的代码.

a = np.array([[0, 1/2, 1, 0], 
              [1/3, 0, 0, 1/2], 
              [1/3, 0, 0, 1/2], 
              [1/3, 1/2, 0, 0]])

a 是我们的状态转移矩阵, 你可以把它理解成就是咱们之前说的M, 对角线为 0 就下一时刻它不能自己走到自己. w 就等于最开始的那个 1/4, 每个顶点都等于 1/4.

一开始为 w, 然后 w 要乘上 a, 也就是乘上那个转移矩阵M. 乘完以后我们把这个状态打印出来. 我们假设一直循环 100 次, 看它迭代的一个结果.

def work(a, w):
  for i in range(100):
    # 每次求解 w, 是向量
    w = np.dot(a, w)
    print(w)

work(a, w)

---
[0.375      0.20833333 0.20833333 0.20833333]
[0.3125     0.22916667 0.22916667 0.22916667]
...
[0.33333334 0.22222222 0.22222222 0.22222222]
...
[0.33333333 0.22222222 0.22222222 0.22222222]

运行一下, 从打印结果可以看到, 1/4 之后我们就发现一些变化. 再之后也继续发生变化, 等到几个轮次之后它已经稳定了. 我这边数一下大概是在 22, 23 次左右. 稳定之后, A 就是等于 0.333..., B, C, D 都等于 0.22..., 后面已经不再发生变化了. 也就意味着不管运行多少次, 响力也都是跟之前是一样, 那么基于这种方法, 我们可以对 A B C D 去做个排行.

那么只要我们能去构造一个大的网络, 页面和页面之间是有连接的. 谷歌是先有一个爬虫, 爬虫就通过页面的链接去爬. 如果 A 它上面有个外链链接到了 B 和 C, 那么它就可以爬到 B 和 C. 在页面和页面之间理论上都是有关联的.那么这个关联就可以把它看成一张大图, 看成大图之后我就可以按照刚才这套原理不断的去模拟, 不断去进化. 达到一定次数以后你的影响力就会显现出来.

其实从刚才那张张图上面也能看出来 A 是一个比较核心的节点, 所以它影响力就会更大一些.

随机浏览模型

这个简化版的模型在实际的工作中有没有一些缺陷, 这是我们要去思考的. 最后拉里佩齐也证明是有两种缺陷的, 分别称之为叫做"等级泄露"(Rank Leak)和"等级沉没"(Rank Sink).

因为简化版模型会有一个前提, 就是一个顶点既要有出度又要有入度. 图上也显示出了每个点都有出度和入度. 以 C 这个简单一点的为例, 它是有出度同时也有入度. 任何点都是一样的.

但是如果我们变化一下, 那在现实的生活中或现实的工作中去做这个页面的抓取, 一定都满足既有出度又有入度吗?

有没有可能存在这样的一个状态: 只有出度没有入度.

比如你写了一个新的页面放到了网站上, 链接了别人. 但是网站上没有其他人链接过我, 有没有可能? 存在这个可能性的.

那存不存在另一种可能性: 只有入度没有出度.

比如别人都去引入我, 但是在我的文章中没有引入别人. 对于网页来说也是存在这种可能性的.

如果存在了这样的可能性会导致什么样的结果呢? 我们先看第一个: "等级泄露".

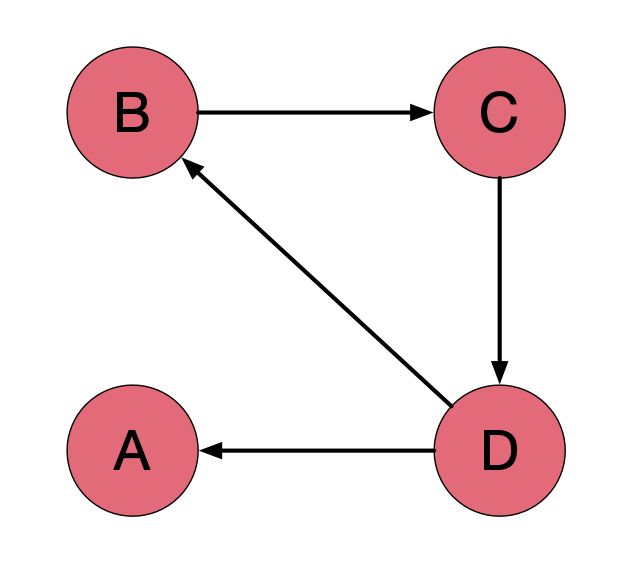
上面这四个顶点里面 A 就没有出路, 没有出路我的影响力下一个过程是释放不出去的. 影响力下一次出不去, 那整个这个网络还会有效吗? 出不去也就意味着我们只能吃不能出, 吃的是 D 的影响力, 只要 D 有影响力的话都给了 A, 那 A 就像是黑洞一样, 吸收了所有的影响力而不释放, 所以你可以把这样的一个过程叫做黑洞的过程.

如果存在了这样一个黑洞, 这个网络就没有效. 因为其他的影响力只要存在都会逐渐的被 A 吸走, A 吸走以后就发现 B C D 都为 0 了. 整个过程中 B C D 也无法进行排名和排序, 这种状态就会导致其他网页的 PR 值为 0.

好除了以上这种状态以外还有一种状态叫做"等级沉没".

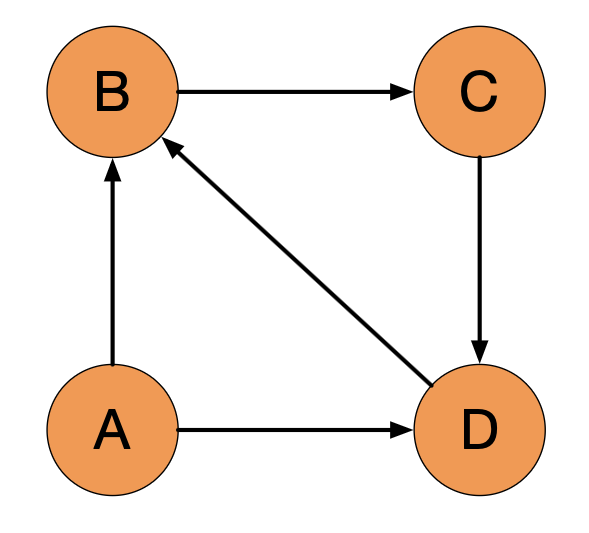
还是看 A, A 只出不进. 只出不进就有点像雷锋一样, 只做好事不求回报. 那么也就没有人去链接他, 他就会把自己影响力给到所有的人. 迭代一百次或者一千次, 很多很多次之后 A 的影响力会是多少? 一开始 A 是有一点影响力的, 但是每次计算过程中影响力都会释放出去, 迭代了很多次以后 A 的影响力就变成了 0. 在搜索引擎里面这个页面就没有了.

在这个过程中 A 在搜索引擎已经没有了, 相当于这个页面就消失了一样, 也不是我们想要的, 我们希望要对它来做个排序.

因此简化版的模型需要既有出度和又有入度, 在现实过程中, 假设不是所有的网页都存在出度和入度, 那么就会像黑洞一样把所有人都吸走, 要么像雷锋一样, 最后自己的影响力就为零, 这都会导致整个的网页的排序 PageRank 失效.

那该怎么做呢? 拉里佩奇最开始的时候想, 要不要就把一个点去掉, 去掉以后再去计算其他的点, 计算好了再把这个点给它加进去. 这种方式在某些情况下确实能解决问题, 但是也有些情况是解决不了的. 比如咱们把第二张图, 也就是等级沉没那张图改一下:

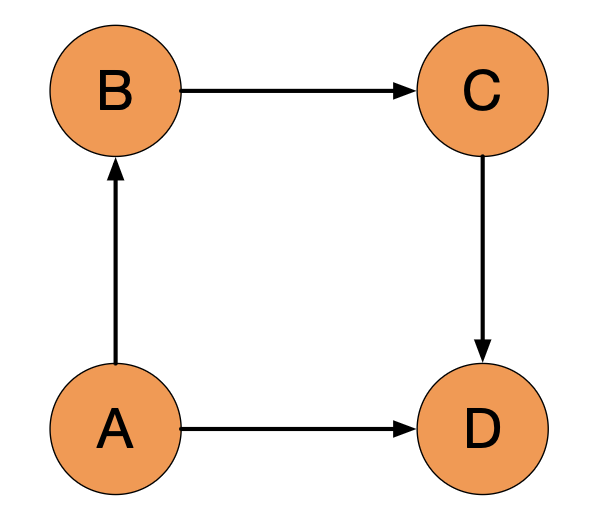
我们看一个图, 在原来的基础上, 我去掉了 D 到 B 的连接. 那 D 到 B 也就没有连接了, 我们把 A 去掉, 然后现在的影响力, B 到 C 到 D, 它还是存在雷锋和黑洞, 就还要再去掉一个.

所以这种治标不治本的方式发现去掉一个节点之后还会引入到其他的一些问题. 就有点像我们写程序找 bug 一样, 刚把一个 bug 解决掉了发现又有新的 bug 产生了. 所以在工程上面它是一种治标不治本的方法, 无法一次性的解决.

为了去掉一个顶点可能会引用到新的问题, 那并不是我们最终的解决方案. 那有没有一些方式可以很好的去解决影响力为 0, 或者无法计算的问题? 拉里佩齐就提出来一种"随机浏览"的模型.

它假设用户其实并不是完全按照跳转链接来进行上网的. 之前我们是完全跳转链接, 如果按照某种跳转链接的方式有可能存在黑洞和雷锋的情况就导致网络失效.那么如果我们还有一些可能, 就是不管你现在在哪个页面我都可以直接在浏览器的网址上面输入其他页面, 那我们就有一定的概率去访问到任意的页面.

这个在我们上网过程中也比较符合逻辑, 你上网过程中不一定都是按照页面跳转来进行完成, 有些情况下你知道要看哪些页面, 直接输入网址也是一种方式.

那么这些方式的过程中怎么做呢? 拉里佩奇就引入了一个参数, 阻力因子"d".

原来的简化版模型还是有效的, 我们给它设一个比重权重"0.85", 剩下的 15% 就采用随机变量模型. 那页面上面如果有 100 个网页, 我们就把这一百个网页平分 15% 的影响力. 也就意味着在下一时刻, 会有 15% 的几率会随机的去跳转到这个页面上. 对于任何的页面 u, 我们就有两部分组成, 一部分叫做随机的概率, 一部分跳转的概率, 由两块来进行组成.

\[ PR(u) = \frac{1-d}{N} + d\sum_{v\in {B_u}} \frac{PR(v)}{L(v)} \]

这样的一个方式是否可以解决问题呢? 我们来做个实验, 还是用刚才那段 Python 代码来做一个模拟, 这次我们加上一个随机的概念.

我们用原来的那个图来去看一看, 如果你用一个随机的模型, 85%用于简单的模拟, 15%用于随机的模拟, 原来 A B C D 的影响力会不会发生变化.

# n 代表网络中的 page 个数
def random_work(a, w, n):
  d = 0.85
  for i in range(100):
    # 随机浏览模型,让节点每次不会等于 0
    w = (1-d)/n + d*np.dot(a, w)
    print(w)

random_work加了一个随机的概念, d是阻力因子, 还是 w 乘上 a, a 是转移矩阵. 有 85% 是来自于转移矩阵的影响力, 还有(1-d)是来自于随机浏览. 然后打印下 w.

random_work(a, w, 4)

---
[0.35625    0.21458333 0.21458333 0.21458333]
...
[0.3245614 0.2251462 0.2251462 0.2251462]
...
[0.3245614 0.2251462 0.2251462 0.2251462]

还是转移矩阵 a, 然后打印 100 次. 运行下来的结果可以看到, 大概从 20 次左右开始没有变化了, 最终已经收敛. 但这个值跟刚才的值会发生一些区别.

原来 a 是 0.333 后面都是 0.22, 现在这个值会发生一些区别.

虽然绝对值发生了一些区别, 但是在排名上面还是 a 是最好. 所以加上了随机模型, 如果页面是一个规整的页面, 都有出度和入度, 排名是不会发生变化. 从这个例子上面可以看到 a 还是最好的, b c d 是同样第二好.

那我们要解决的是一个"等级泄露"和"等级沉没"的问题, 接下来我们从新定义两个矩阵:

a_leak = np.array([[0, 0, 0, 1/2], 
                   [0, 0, 0, 1/2], 
                   [0, 1, 0, 0], 
                   [0, 0, 1, 0]])

a_sink = np.array([[0, 0, 0, 0], 
                   [1/2, 0, 0, 1], 
                   [0, 1, 1, 0], 
                   [1/2, 0, 0, 0]])

a_sink这个值里面就相当于有一些边没有链接, 没有入点. 那么拿这样的一个图, 用原来的经典模型简化版模型来去做计算, 就会发现整个页面失效了.

work(a_sink, w)

---
[0.    0.375 0.5   0.125]
[0.    0.125 0.875 0.   ]
[0. 0. 1. 0.]
...
[0. 0. 1. 0.]

有一个为 1, 其他都为 0. 那这样在做排序的时候, 其他页面就出现不了, 只能出现一个. 这并不是我想要的.

现在我们来用random_work去做.

random_work(a_sink, w, 4)

---
[0.0375  0.35625 0.4625  0.14375]
[0.0375    0.175625  0.7334375 0.0534375]
[0.0375     0.09885938 0.81020312 0.0534375 ]
...
[0.0375     0.09885938 0.81020312 0.0534375 ]

可以看到, random_work是把它分成随机浏览和经典模型两个部分来做, 组成以后它的数据到后面已经发生了收敛. 除了原来最大的那一个还是最大的, c 是 0.81 排到第一名, 第二名是 b, 第三名是 d, 第四名呢是 a. 这样就解决了原来的"等级沉没"的问题.

同理, 再去看一个"等级泄漏"的问题.

从a_leak这个矩阵里面可以第一列都为 0, 没有出链, 出不去. 那这个状态是一个leak, 先用经典模型去做一个计算.

work(a_leak, w)

---
[0.125 0.125 0.25  0.25 ]
...
[1.45519152e-11 1.45519152e-11 2.91038305e-11 2.91038305e-11]

计算完以后可以看到, 经过 100 轮之后看到这样一个数据. 1.45519152e-11中, -11是一个科学记数法, 所代表的就是 10 的负 11 次方, 10 的负 11 次方几乎就为 0. 当运行次数越多的情况它就基本上等于 0, 到后面如果都等于 0, 整个网络就失效了, 它也无法来进行排序.

这种情况下还是要用到random_work来帮你去解决.

random_work(a_leak, w, 4)

---
[0.14375 0.14375 0.25    0.25   ]
[0.14375   0.14375   0.1596875 0.25     ]
...
[0.09667099 0.09667099 0.11967748 0.13922586]
...
[0.09666727 0.09666727 0.11966718 0.1392171 ]

还是分成两块, 随机的部分加上经典的部分一起来运行一下. 因为它有随机的部分, 所以至少还是会有值的. 最终可以看到它结果的状态, 这个结果状态可以看到 d 是最高的, 其次是 c, 之后就是 a 和 b. 因此我们是可以对页面去做排序.

从刚才的过程上可以看到, 加上了一个随机浏览的部分可以让每一轮的计算 A B C D 页面上都会有一些影响力, 即使这个影响力被分配的很少, 但是它不为零. 那进行初始化以后, 就可以对这些所有的页面来做个排序, 也就解决了之前网页排序失效的问题.

以上的内容, 就是随机浏览模型的全部内容, 一个很巧妙的方式, 由两部分组成. 那我们也就将 PageRank 这两种模型都给大家讲完了. 这个就是十大经典机器学习的影响力排序模型.

下一节课, 我们来看看 PageRank 延伸的一些影响力, 包括社交, 职场以及生物领域等等, 然后咱们再回到推荐系统, 看看 PageRank 是如何来影响推荐系统, 在其中发挥作用的.