26. BI - PageRank 拓展以及如何利用 networkx 来分析希拉里丑闻

本文为 「茶桁的 AI 秘籍 - BI 篇 第 26 篇」

[TOC]

Hi, 我是茶桁.

上节课咱们讲解了 PageRank 的两种模型, 并分别做了代码上的演示. 这节课, 让我们来看看 PageRank 的影响力及其应用.

PageRank 已经超越了原来提出来的模型, 因为 PageRank 的影响力影响到了后续很多的一些模型, 都可以采用它. 举个例子, 最早是在论文里面使用, 之后在网页里面使用, 现在还可以在社交网络里面使用.

比如微博, 如果一个微博的博主的粉丝量有 10 万个, 那他影响力一定大吗? 10 万粉丝的博主, 有 10 万人关注, 你可能觉得这个影响力确实很大. 但有没有一些可能他的影响力并不大? 存在这种可能性吗?

大家知道, 其实有些粉丝并不活跃, 我们把它称为叫做僵尸粉. 在淘宝上面据说有一些在卖僵尸粉的, 1 万个粉丝可能几块钱或者十几块钱.

如果你要去做到一个十万粉丝的一个博主其实并不难, 这里我指的加上很多的僵尸粉. 假设这些粉丝都没有什么活跃度, 这个博主还有影响力吗? 就不一定.

所以在社交网络中如果要去衡量一个博主实际的影响力, 不能只看粉丝的数量, 还要看粉丝的质量. 如果质量比较高, 影响力就比较大.

再举个例子, 如果一个微博的博主粉丝刚开始的时候只有 500 个, 但是这 500 个粉丝都是一些有影响力的人, 比如像李开复, 马云等等. 那么他的影响力大不大? 影响力一定会很大. 而且后面粉丝数肯定也会越来越多, 因为他的粉丝的影响力大, 关注了这个人就相当于把票数投给了这个人, 在 PageRank 方式里面再去计算影响力过程中, 就比简单的只看粉丝数效果好很多.

脉脉这个软件对标的是国外的 LinkedIn, 也是个职场社交的软件. 脉脉在你进去以后会扫描你的手机通讯录, 然后会给你打一个影响力的分数. 他告诉你在行业中的影响力是多少.

猎头在脉脉上, 很多你的身边的同事也在脉脉上, 脉脉就可以看到自己的影响力, 也可以看到别人的影响力. 这个影响力的计算你可能会好奇他怎么算出来的, 实际上这个影响力的计算就是跟 PageRank 相关.

你会发现明星的影响力都很高, 但他的计算又是基于手机通讯录. 其实一个人的手机通讯录都不会太多, 可能 5,000 个人, 一万个人就顶天了. 但是怎么样能看出来有的人影响力能有几万的影响力, 有的人影响力只有十几. 这里的差距可能有成百上千倍的一个差距.

就是因为你的通讯录那些人的影响力的高低来决定了. 如果你的通讯录都是一些大老板, 是一些企业家或者是一些投资人, 再或者是一些明星. 那你的影响力就会很大.

所以只要你跟有影响力的人在一起, 你的影响力就会大很多. 从这个例子上面也能告诉我们, 在职场上面你要社交的话, 如果在社交链路上是跟 100 个底层的员工都是好朋友, 他在公司里面影响力大吗? 再换另一个人, 他跟 10 个高管都是好朋友, 数量其实并不多, 谁的影响力会更大? 是第一个人还是第二个人?

从整个 PageRank 的算法过程中, 如果你按照这个指数来进行计算, 它其实看的并不是整个的数量. 第二个人虽然他的数量比较少, 但是结识的都是一些高管, 高管的影响力比较大. 所以影响力也很大.

所以同样在生物领域里面, PageRank 也可以帮我们去确定哪一个基因是关键. 它可以帮我们来去确定跟遗传相关的肿瘤基因, 去定位, 做生物领域的一些研究.

还可以在推荐系统里面, 帮我们给用户去做一个推荐. 这里的推荐需要转化成图. 因为他要分析的是一张图中的影响力的关系.

PersonalRank

那到底是怎样跟推荐系统相关呢? 给某一个用户进行推荐就相当于要计算用户和所有商品之间的一些相关性, 然后把那些它没有连接的物品从高到低生成一个列表, 这是整个的一个逻辑.

具体怎么做? 我们来看下面这张图:

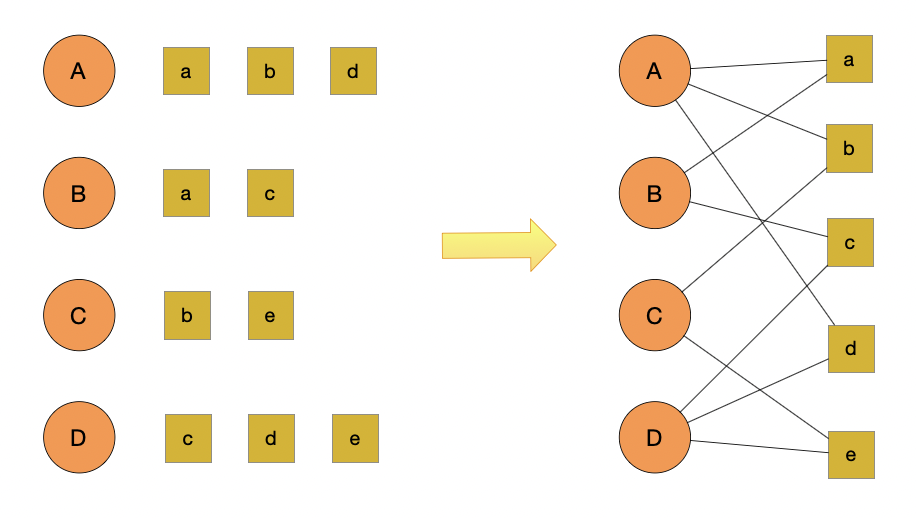
整个这张图我们把它分成两个部分, 一个叫用户 user, 一个叫商品 item. 用户是大写的 A B C D, item 是小写的 a b c d e.

在推荐系统里面用户和商品之间是有些关系的, 比如点击行为. 点击行为是属于隐式的关系. A 它点击了 a b d, B 点击了 a 和 c 等等.

这张图可以用一个"二部图"分成两个部分, 左侧是所有的用户, 右侧是所有的商品. 如果发生了点击, 就用一张无向图, 没有方向的图来做一个连接. 可以到 A 是和 a b d 做了一个连接, 把它做成了三条边的连接.同样 B 是跟 a 和 c, C 是和 b 和 e, D 是跟 c d e. 这样我们就把边给连接好了.

我们现在来思考, 如果把边连接好能不能去计算顶点的影响力? 其实只要有了图, 就可以计算影响力, 因为连接边就相当于把票数给了别人, 所以这个过程是可以计算影响力了.整个的原理是, 如果你要给用户 A 来做推荐, 就相当于把 a b c d e 去做一个排名的关系, 排名以后 a b d 这三个商品都已经浏览过了, 所以重点是看 c 和 e 的排名. 如果 c 的排名高推荐顺序就是先推荐 c, 再推荐 e, 这就是针对 A 来做推荐.

那这整个的算法被称为 PersonalRank, 它也是基于 PageRank 产生的一种推荐算法, 是把用户和商品看成一张二部图, 中间的行为会形成一条边. 要针对某一个用户做推荐实际上就是对所有的商品去做排序, 然后去掉 A 已经看过的商品. 这就是 PersonalRank 的一个原理.

具体怎么去套 PageRank, 其实它还是有一个公式.

\[ \begin{align*} PR(V_i) = \frac{1-d}{N} + d \sum_{V_j \in ln(V_i)} \frac{PR(V_j)}{|Out(V_j)|} \end{align*} \]

首先这是一个随机浏览模型, 可以看到它原来的模型是两部分组成, 把所有的影响力都平均分配给网络上的 N 个节点.

现在也用随机的模型, 只不过现在随机不是一个纯随机, 是每次都从固定的顶点开始. 如果你是给 A 来做推荐那就只针对 A.

\[ \begin{align*} & PR(V_i) = (1-d)r_i + d \sum_{v_j \in ln(V_i)} \frac{PR(V_j)}{|Out(V_j)|} \\ & r_i = \begin{cases} 1 \qquad i=u \\ 0 \qquad i \ne u \end{cases} \end{align*} \]

比如说现在给用户 u 做推荐, 那对于 u 来说它为 1 是 100%, 下一步都给 u, 如果不是 u 就为 0%, 下次不点击你. 那这是一个初始化的过程, 我们将用户 u 设为 A, 就如上图, 有 A B C D 四个用户. 目前是对 A 做推荐, 那我们初始化值就是PR(A) = 1, PR(B) = 0, PR(C) = 0, PR(D) = 0, PR(a) = 0, PR(c) = 0 , ... PR(e) = 0. 也就是说, 我们并不区分用户和商品, 仅仅是把它当作一个节点, 要对通过连接的边为每个节点打分.

然后我们就要开始游走, 从不为 0 的节点开始, 那我们因为是对 A 做推荐, 初始化值PR(A) = 1, 沿着边游走的概率为d, 停在当前点的概率为1-d.

此时 PR 值不为 0 的节点就为 A, a, b, d, 然后我们从这三点触发, 继续上述过程, 直到收敛为止. 当收敛的时候, 计算 item 节点影响力, 把影响力做个排序, 排序以后去掉 A 已经看过的一些商品, 最终就可以给 A 做推荐了.

它的核心是如何去转化成一张图, 如果把它看成一张图, 图里面就自带 PageRank 的模型, 自带影响力的排序, 就可以给用户去做推荐了. 这是基于图论的一种推荐方法.

pageRank 的影响力还不仅仅是 PersonalRank, 还有很多的一些影响力. 很多种模型都是基于它来产生的衍生. 刚才看到的是 PernalRank, 还有哪些模型跟它有关系?

还可以做交通网络, 交通网络就是一张图, 图里面会有顶点, 哪个顶点影响力高就意味着这个人流往哪里, 那个地方就是交通的枢纽. 在交通网络里面也有影响力的排名.

PageRank 工具使用

对于这些 PageRank 的应用我们该怎么去使用? 我们可以使用的工具也蛮多的, 我们先来看第一个: igraph. igraph 的性能会比较强大, 效率比较高.

除此之外, 我们还有第二工具NetworkX. 这个工具是基于 Python 的一个库, 对于使用者来说非常友好, 如果你是 Python 的使用者建议使用第二个库.

这两个库的作用是一样的, 使用NetworkX是因为它对 Python 的接口非常友好. 如果数据量非常非常的多, 节点超过了上百万个, 可以使用igraph. igraph的效率会更加的强大.

通常如果顶点数量不是很多用NetworkX还是比较好用的. 而且NetworkX除了 PageRank 这个模型, 还集成了很多其他的图论模型.

我们还是来看一个示例, 咱们上一节课有一个有向图:

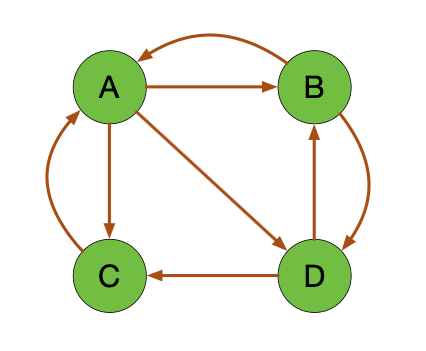
咱们就用这个图中 A B C D 的影响力排序来看一看, 怎么样去调NetworkX这个包.

首先, 创建一个有向图. 有向图的叫Directed Graph, 有方向的含义.

G = nx.DiGraph()

当我们看到一张图就要有意识, 一个图的组成是由边和顶点. 所以一张图你可以把它看成顶点和边的一个集合. 如果我们把边都规定出来, 线上面有点, 那么这张图就出来了.

现在我们来看上面这张图, 它是一个有向图, 所以边是有顺序的. 顺序是边指向的方向, 这些过程都是一个有顺序的过程. 比如说从 A 到 C, 那就写成(A, C), 据此, 我们可以写出这个有向图的一个边的关系:

edges = [('A', 'B'), ('A', 'C'), ('A', 'D'), ('B', 'A'), ('B', 'D'), ('C', 'A'), ('D', 'B'), ('D', 'C')]

然后把所有的边做一个累加. 写一个循环, 前面是起点, 后面是终点. 把边都加到了图里面去, 这张图就建好了, 只要图建好了就可以做 PageRank.

for edge in edges:
  G.add_edge(edge[0], edge[1])

现在先用一个精简模型, 精简模型是 100%都用于模型, 没有随机浏览的部分. 所以阻尼因子不是 0.85 了, 而是 1. 在 PageRank 里面, 阻尼因子的参数是Alpha, 把Alpha设为 1, 调networkx.

pagerank_list = nx.pagerank(G, alpha=1)

原始数据就是G, 刚刚创建好的这张图. 通过它的配置可以计算出来, 得到一个pagerank_list, 这个就是 PR 值.

print('pagerank 值为: {}'.format(pagerank_list))

---
pagerank 值为: {'A': 0.33333396911621094, 'B': 0.22222201029459634, 'C': 0.22222201029459634, 'D': 0.22222201029459634}

打印一下, 看到最终的结果. 上一节课中, 咱们是自己去写的模拟, networkx则是集成了这个包, 调用起来也非常的方便.

networkx还有一些可视化的功能, 我们直接先去做一个layout, 就是布局采用怎样的布局的形式. 重要是把这张图画出来.

layout = nx.spring_layout(G)
nx.draw(G, pos=layout, with_labels=True)

position 等于 layout, 指定 layout 方式. with_labels, 要不要 label. 然后给它画出来:

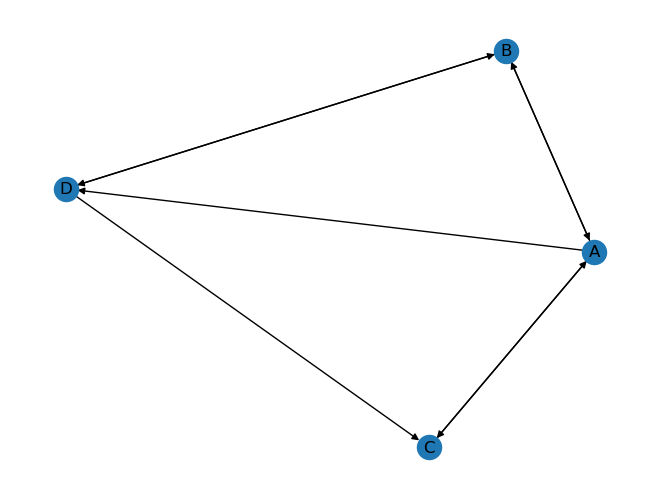
那同时还可以设置一下随机模型, 只要把alpha设成 0.85 就可以. 同样, 我们修改程序之后再来运行一下, 看到打印的结果.

pagerank_list = nx.pagerank(G, alpha=0.85)
print('pagerank 值为: {}'.format(pagerank_list))

---
pagerank 值为: {'A': 0.3245609358176832, 'B': 0.2251463547274389, 'C': 0.2251463547274389, 'D': 0.2251463547274389}

我们展示的图实际上跟之前我手工绘制的那个图是完全一致的, 边的逻辑关系是一样的.

可视化之后, 我们打印出来的值跟之前计算的也是一样的. 在精简模型中 A 是 0.333, B C D 都是 0.222. 如果把阻尼因子设成 85%, 得出来 A 比较大, 后面 B C D 也是相等的.

networkx的逻辑就是先创建数据, 往里面加上各种边. 有了边, 图就出来了, 可以做可视化. 同样只要一句话, 就可以去调 pagerank 的结果, 这个结果就是个字典, 因为 pagerank 是对网页做排序, 其实得出来的结论就是一个网页的影响力. 我们就用字典的形式把这个结果做了一个保存.

后面咱们套这个模型, 想一想怎么样先转化成一张图, 有了图最终调包就是一句话的事.

还有一些情况可以用networkx, 是直接可以把一张图给它读进来. 这里可能就需要用到一些特殊的格式, 有一个gml的格式, 就是graph XML, 它的编码形式呢就是一张图, 因为有的时候图会很复杂, 一个一个去加时间也会很长, 不如直接从图文件来进行加载. networkx也是支持直接加载的功能.

刚才咱们的示例中, 创建的是一个有向图, 用了DiGraph方法, 如果需要创建无向图, 可以使用Graph方法: nx.Graph(). 包括我们还可以对节点进行一些操作, 增删改查:

• 添加节点: 使用G.add_node('A'), 也可以使用G.add_nodes_from(['B', 'C', 'D', 'E']), 区别就是加一个顶点和加一群顶点.
• 删除节点: 使用G.remove_node(node), 也可以使用G.remove_nodes_from(['B', 'C', 'D', 'E']).
• 节点查询: G.nodes()获取途中所有节点, G.number_of_nodes()获取途中节点的个数.

这些都是比较常使用的一些, 然后就是我们可以对边做一些操作:

• G.add_edge('A', 'B')添加制定的从 A 到 B 的边
• G.add_edges_from从边集合中添加
• G.add_weighted_edges_from 从带有权重的边的集合中添加

以上都是边的添加, 参数就是 1 个或者多个三元组[u, v, w]作为参数, u, v, w 分别代表起点, 终点和权重.

那什么是有权重呢? 之前认为边的权重都是相等的, 但有些时候这个边你可以给它设一个权重, 设了权重就代表可以把它看成多条边或者可以把它看成影响力更大的一种走法.

我们再去用add_weighted_edge的时候, 就要使用三个元素, 除了两个顶点 u 和 v 以外, 还有 w, 就是权重. 比如, 咱们说一个关于邮件的例子, a 到 b 两个人如果经常写邮件, 和 a 到 b 只写过一次邮件还是不太一样的.

经常写邮件就证明这条通路很大, 权重大, 所以权重就会高. 它就可以表明 a 到 b 转移的概率不是一个平均分配, 而是一个有权重性的分配方式.

除了加上这个边以外, 我们还可以去删除或者删除一群边, 方法为G.remove_edge以及G.remove_edges_from.

还可以对边进行查询, G.edges()是获取图中所有边, G.number_of_edges()是获取图中边的个数.

这两个跟点的方式是完全一样的.

我们在进行可视化的过程中, 我刚才示例了一个spring_layout方式, 除此之外其实还有其他的一些形式, 包括nx.circular_layout(), nx.shell_layout(). 大家可以自己跑一下试试, 我这里就不做示范了.

你选择一个适合的方法, 当你的边数很多的情况下, 不同的样式呈现出来也会有一些区别. 以下是它们的一些区别:

• spring_layout: 中心放射状
• circular_layout: 在一个圆环上均匀分布节点
• random_layout: 随机分布节点
• shell_layout: 节点都在同心圆上

希拉里邮件丑闻

咱们来看一个例子把, 这个例子是希拉里邮件的丑闻. 相信大家应该都知道这个故事是一个什么样的事件. 故事发生在 2016 年, 当时应该是希拉里和特朗普在竞选美国的总统. 竞选过程中希拉里一直是领先的, 后来爆出来一个丑闻, 发现一共有 9,300 多封邮件和 513 个人. 马上要大选了, 9,000 多封邮件, 500 多个人, 如果每个人都进行庭审的话可能一年的时间都不止. 法官就找到了一个科技公司, 帮着想办法找到最关键的 20 个人, 这 20 个人作为最开始的庭审的对象.

那怎么样去找到这关键的一些人物, 这个科技公司就想到了使用 PageRank. 因为我们可以把邮件的往来看成一个网络, 这个网络里面每一个人都是个顶点, 每封邮件都是一条边, 就有 9,000 多封电和 500 多个顶点.

数据是三个文件, 一个是原始的记录Email. 发邮件的时候有时并不写它的全称, 会有些昵称, 所以单独还有个Aliases来存储一些邮件的别名, Persons统计了邮件中所有任务的姓名及对应的 ID.

那怎么样去数据里面挖掘那些有影响力的一些人呢? 我们先来看一下原始的数据

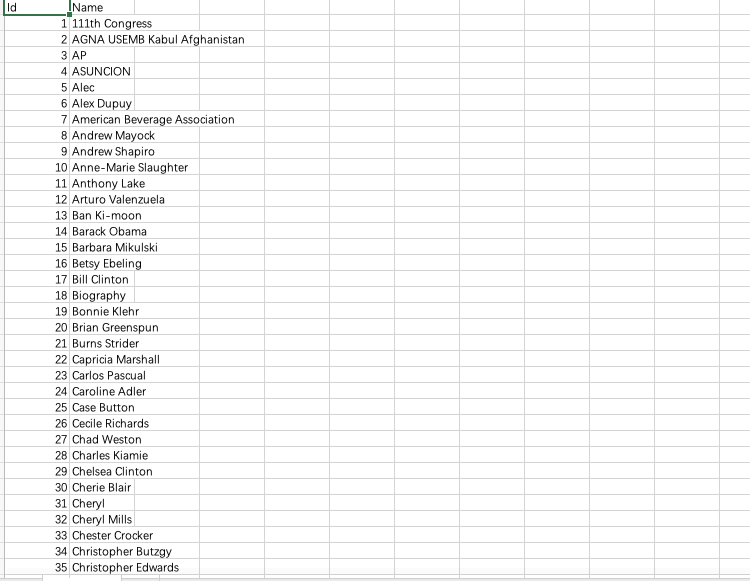
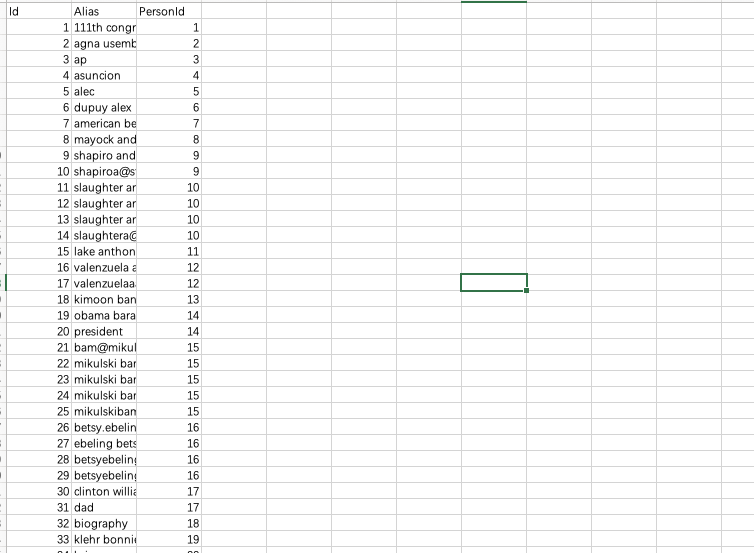
Emails上面有很多的表头, 真正要用的主要是两个, 一个就是它的发件人, 一个是它的寄件人. Persons对做了一个 ID 的处理, 比如叫什么名称. 但一个人可能会有很多别名, 因此还专门有个Aliases, 哪些别名最后指向的是哪个PersoID都会给它一一做记录.

所以我们把别名和persoID作为关联, 可以看到persoID是最关键的一个信息, 同时具体的name在哪里, 都是通过persoID来作为关联.

在 Emails 里有几个比较关键的信息, 一个就是MetadataTo, 一个是Metadata From, 这两个信息代表的是从哪一个人到哪一个人, 当然后面还有具体的一些content.

我们今天不去看具体的 content, 主要是看人物的关系, 如何去把它变成一张图.

原始数据emails文件比较大, 但是真正关心的数据只有两列: from和to.

我们先来对原始数据做一个加载:

# 数据加载
emails = pd.read_csv('dataset/pagerank/Emails.csv')
# 读取别名文件
alias_files = pd.read_csv('dataset/pagerank/Aliases.csv')
# 读取人名文件
person_files = pd.read_csv('dataset/pagerank/Persons.csv')

现在咱们需要做一个字典, 把所有的别名跟persoID做一个关联. 读出来的alias和persoID之间的关系, 然后又读取了一个persons, 这里存储的是persoID和name之间的关系.

aliases = {}
# 别名 => PersonalID
for index, row in alias_files.iterrows():
  aliases[row['Alias']] = row['PersonId']

persons = {}
# PersonID => Name
for index, row in person_files.iterrows():
  persons[row['Id']] = row['Name']

那么任何的名称都可以找到 ID, ID 呢又可以找到 name, 就需要写一个函数来去做一个变化.

# 针对别名进行转换 Alias => Name
def unify_name(name):
  # 姓名统一小写
  name = str(name).lower()
  # 去掉`,`和`@`后面的内容
  name = name.replace(',', '').split('@')[0]
  # 别名转换
  if name in aliases.keys():
    return persons[aliases[name]]
  return name

第一个name进来以后去掉一些不相关的一些内容, 然后看aliases里面有没有, 如果有最终转化出来. 就是把alias转化到name, 然后返回出来.

看这个逻辑, 原来是一个alias的一个name转化成一个persoID, 再把persoID转化成一个name, 这样对别名做了一个清洗.

之后我们就要来绘制一张网络图, 为此我们来写个方法, 方便后面进行调用

def show_graph(graph, type='sprint_layout'):
  pass

在图里面可以制定不同的一些layout, 咱们用type来接收, 并在其中做一个判断, 来确定具体使用哪一个方法:

if type == 'sprint_layout':
  # 使用 Spring Layout 布局, 类似中心放射状
  positions = nx.spring_layout(graph)
if type == 'circular_layout':
  # 使用 Circular Layout 布局, 在一个圆环上均匀分布
  positions = nx.circular_layout(graph)

然后就是丰富一下这个方法, 将绘制内容添加进去

# 设置网络图中的节点大小
nodesize = [x['pagerank']*20000 for v,x in graph.nodes(data=True)]
# 设置网络中的边长度
edgesize = [(np.sqrt(e[2]['weight']))/5 for e in graph.edges(data=True)]

fig, ax = plt.subplots(figsize=(12, 8))
# 绘制节点
nx.draw_networkx_nodes(graph, positions, node_size=nodesize, alpha=0.4, ax=ax)
# 绘制边
nx.draw_networkx_edges(graph, positions, width=edgesize, edge_color='r', alpha=0.5, ax=ax)
# 绘制节点的 label
nx.draw_networkx_labels(graph, positions, font_size=10, ax=ax)
# 输出邮件中所有人物关系图
plt.show()

提取信息的时候, 是从emails里的提取MetadataFrom和MetadataTo, 我们apply刚才的那个别名转换的函数unify_name().

# 将寄件人和收件人的姓名规范化
emails.MetadataFrom = emails.MetadataFrom.apply(unify_name)
emails.MetadataTo = emails.MetadataTo.apply(unify_name)

那么MetadataTo和MetadataFrom这两个表明的就是整个的name, 从谁到谁. 那具体是哪一个人都用最终的一个name去做关联. 所以name是最后清洗出来的唯一一个人. 因此通过apply的方式去调了一个清洗函数, 把from和to作了一个清洗.

同样人和人之间写邮件有可能是多次, 因此也需要记录一下发邮件的个数. 就用from和to去做一个代表, 然后把from和to这个权重写一个字典, 建一个edges_weights_temp专门记录一下邮件往来的次数. 如果没有就写成 1.

# 设置边的权重等于发邮件的次数
edges_weights_temp = defaultdict(list)
for row in zip(emails.MetadataFrom, emails.MetadataTo, emails.RawText):
  temp = (row[0], row[1])
  if temp not in edges_weights_temp:
    edges_weights_temp[temp] = 1
  else:
    edges_weights_temp[temp] = edges_weights_temp[temp] + 1

print(edges_weights_temp)
print('-'*100)

defaultdict(<class 'list'>, {('Jake Sullivan', 'Hillary Clinton'): 815, ... , ('Hillary Clinton', 'Daniel'): 1})
------------------

就说这里的一封邮件, 看它之前有没有创建, 如果没有创建就为 1, 是第一次记录. 如果有创建就在原来的值上面加 1.

最终可以把它打印出来. 打印出来以后就把它的from和to取出来.

这个结果我们可以看到, 希拉里写了 815 封邮件, 应该写的还是比较多的.

这里我们中断一下, 说一下zip方法. zip是个合并的含义, 那基本上都知道zip原本是压缩, 将一个文件夹或者文件压缩到一起. 这里类似, 相当于把它生成了一个元组.

我们来看一个小的示例, 比如, 我定义三个 list, a, b和c, 先将a, b压缩成zipped.

a = [1, 2, 3]
b = [4, 5, 6]
c = [4, 5, 6, 7, 8]
zipped = zip(a, b)
zipped

---
<zip at 0x15ff7b580>

然后我们来看看zipped的 type 是什么

print(type(zipped))

---
<class 'zip'>

这个时候, 我们可以用list将这个zip转换成列表:

list(zipped)

---
[(1, 4), (2, 5), (3, 6)]

既然是一个list, 那我们完全可以写一个循环, 依次取出 a 和 b 的元素.

for a, b in zipped:
  print('a: {}, b: {}'.format(a, b))

---
a: 1, b: 4
a: 2, b: 5
a: 3, b: 6

那我们还多定义了一个c是做什么用的? 是为了告诉大家, 在使用zip方法的时候, 元素个数与最短的列表会保持一直. c中我们多定义了7, 8, 但当我们对a和c使用zip的时候, 其结果和我们对a和b使用的结果是一致的:

list(zip(a, c))

---
[(1, 4), (2, 5), (3, 6)]

除此之外, 可以使用和zip相反的zip(*), 这个方法可以理解为解压缩, 返回二维矩阵式.

c1, c2 = zip(*zip(a, b))
list(c1)

---
[1, 2, 3]

使用zip必须是可迭代对象作为参数. 你可以把它理解成是两个list, 两个可迭代的部分合并成一起. 我们将其合并一起以后要再去做一个展开, 因为要去得到两个值, 就是 for 循环需要有两个部分, 每次取是一个from一个to. 如果之前写一个负循环, 那第二个内容应该也是个并列的部分. 所以就把这两个部分放到 zip 里面去, 从它里面去取一个, 再从它里面去取一个.

想象成 Excel 里的列, 这样在做遍历的时候就不是一列数据从头到尾了, zip 几个就是几列数据, 刚才是 zip 的三列数据, 一个row就可以有 3 个值了.

我们在做add_weighted_edges_from的时候是一个三元组, 这个三元组分别是from, to和weight三个元素, 那我就可以通过它先去创建一张有向图. 记得要转化一下格式.

# 转化格式(from, to), weight => from, to, weight
edges_weights = [(key[0], key[1], val) for key, val in edges_weights_temp.items()]

# 创建一个有向图
graph = nx.DiGraph()
# 设置有向图中的路径及权重(from, to, weight)
graph.add_weighted_edges_from(edges_weights)
# 计算每个节点(人物)的 PR 值, 并作为节点的 pagerank 属性
pagerank = nx.pagerank(graph)
print('pagerank=', pagerank)
print('-' * 100)

---
pagerank= {'Jake Sullivan': 0.005791704166582628, 'Hillary Clinton': 0.30625575336382355, ..., 'Daniel': 0.0010259982609288146}
------------

最后计算完成应该是顶点影响力的关系, 把每一个影响力都计算出来了. 比如希拉里的影响力是 0.30, 应该是非常高的. 还有 Jack 这个人, 跟希拉里关系应该也不低.

创建一张有向图, 然后把它添加上去. 加上去以后就可以做pagerank的计算了. 把pagerank打印出来就等于整个的影响力的顺序.

打印pagerank是分别有node和rank, 对它做个遍历.

# 获取每个节点的 pagerank 数值
pagerank_list = {node: rank for node, rank in pagerank.items()}

图也可以把它画出来. 调用我们之前写好的绘图方法

# 将 pagerank 数值作为节点的属性
nx.set_node_attributes(graph, name='pagerank', values=pagerank_list)
# 画网络图
show_graph(graph, 'sprint_layout')

我们使用的是sprint_layout这种方式, 把这张图的大小跟pagerank的value做了一个关联.

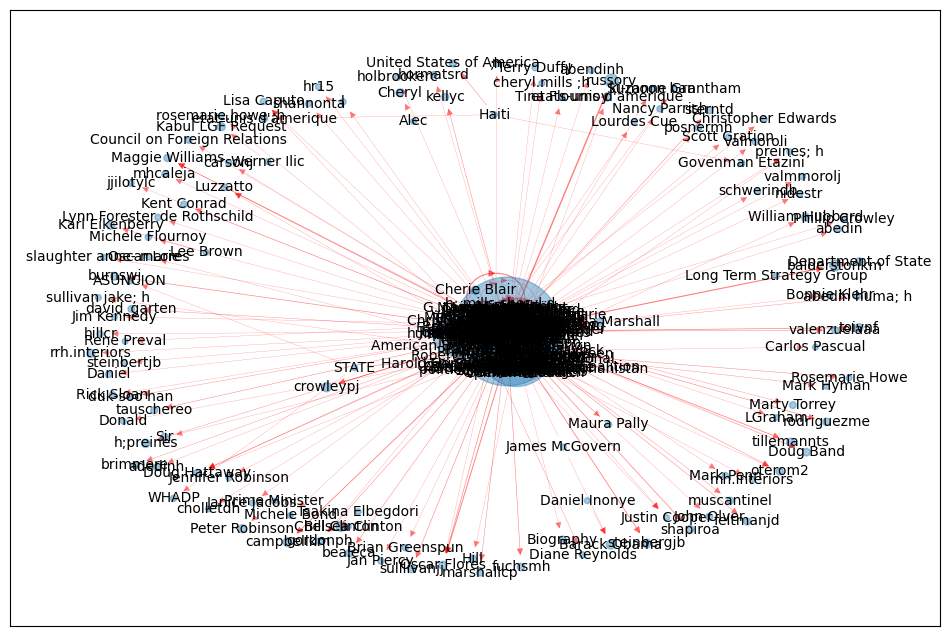
如果我们把 500 多个人都在一张图上面进行绘制的话是看不清楚的, 9,000 多条边很难看清楚. 虽然已经选择了最合适的布局, 但是很难去看清楚.

那我们要怎么做, 把所有的人都显示出来需要一张超大的图, 不好看. 所以在一个宏观的粒度上面如果要把它显示的清晰一点, 咱们去做一个拆解. 可视化比较清楚, 但是可视化咱们又不能显示这么多的边和顶点. 所以要去做一个事情, 就是过滤掉那些不重要的顶点和边.

要找到那些关键人物, 就是法官最开始那个请求一样. 怎么样去过滤呢? 那过滤的过程中可以对影响力做个排序, 比如要取前 20 个人排序, 可以设置一个影响力的阈值, 这里阈值是一个参数, 可以自己来做调整.

# 设置 PR 值的阈值，筛选大于阈值的重要核心节点
pagerank_threshold = 0.005

现在设的是一个0.005, 也就是千分之五, 乘上 200 大概就等于 1, 就只取了千分之五这个粒度.

原来的graph已经格式化出来了, 现在对它做一个copy, 就是再复制一份. 如果用原来的那个graph数据就会发生一些变化, 所以干脆直接复制一份, 在新的这份数据里面做一个记录.

# 复制一份计算好的网络图
small_graph = graph.copy()

现在就直接遍历它所有的顶点, 然后去查询pagerank的值. 不符合要求从图里面给它remove掉. remove之后就变成了一张小图, 再把小图去做一个可视化.

# 剪掉 PR 值小于 pagerank_threshold 的节点
for n, p_rank in graph.nodes(data=True):
    if p_rank['pagerank'] < pagerank_threshold: 
        small_graph.remove_node(n)
# 画网络图
show_graph(small_graph, 'circular_layout')

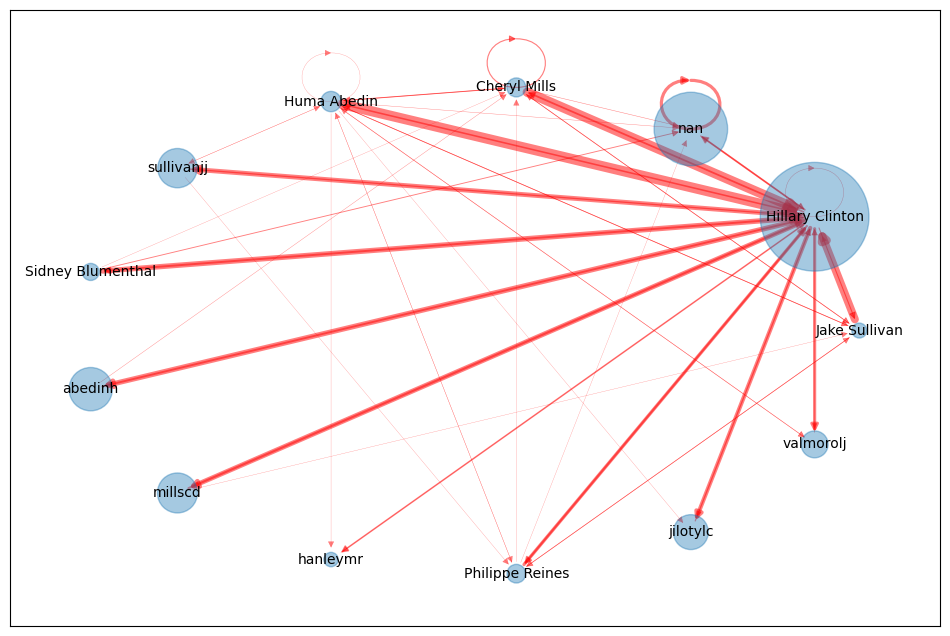
这次我们换了一个circular_layout的布局形式, 把它变成一张小图逻辑就会很清楚了, 最大的那个面积是希拉里, 因为所有人都基本上都会跟她联系.

但是这里面咱们发现也不是所有的人都找希拉里, 他们之间也在相互通信. 所以他们之间也是一个互相链接的一个关系.

这样就可以把影响力的大小从图中很明显的看出来. 那法官要做的事情就是找影响力的人物, 这样就可以对这些最有影响力的人提前去做开庭庭审.

在这个过程中, 首先第一确定模型pagerank; 第二个是前期的数据清洗, 邮件是一个很特殊的例子, 它存在了一些别名的关系, 所以要把它统一名称, 统一人物; 第三个在设置边的转移过程中做一个有权重的边, 因为 a 到 b 之间可能会有多个边, 就是发多封邮件, 多封邮件就代表 a 到 b 属于一个高频的信息. 要做状态转移的时候应该更倾向于邮件次数多的.

最后, 绘制的图如果顶点数很多还可以设个阈值来做一个筛选, 这样呈现出来的图会更加的清爽.

其实这个并不是有多难, 关键的就是怎么样去想到. 还是看pagerank的擅长点, 它擅长的是做排名排序, 而且第二个特点就是图的排名, 排序就是图. 而正好邮件这个事可以看成图, 而且法官的需求就是做排名和排序, 因此用pagerank是最适合不过的.

本次例子中使用到​的数据集也在咱们的代码仓库里， 如果想直接下载数据的可以去这里： https://github.com/hivandu/AI_Cheats/tree/main/Core%20BI/dataset/pagerank