
Hi,大家好。我是茶桁。
上一节课中,我们学习了 matplotlib.
实际上,我们已经进入了数据可视化阶段。
可是在上一节课中,所有的数据都是我们固定写好的,包括两个电影的数据展示的案例(柱状图和直方图),都是我们将数据手动写成了数据列表,然后直接使用。
在我们平时的工作中,不太有那么多的机会使用现成的数据,除非你跟我一样是一个数据产品经理,那倒是会有程序员们会将数据整理好递到你手上。可是即便如此,很多时候我还是需要自己亲手去处理数据,因为我不能为了一次数据验证或者一个什么想法就去惊动程序员为你服务。
更何况,我们现在的课程面向的是人工智能,那么处理数据就成了必须要有的手段,也是家常便饭常有的事。
那么今天,我们就来学习一下 Python
中科学计算的基础第三方库:「numpy」。
简单介绍一下 NumPy

Numpy 的全称是:Numerical Python, 是一个开源的 Python
科学计算库,用于快速处理任意维度的数组。
Numpy 支持常见的数组和矩阵操作,对于同样的数值计算任务,使用 Numpy
比直接使用 Python
要简洁的多。其中的ndarray对象用于处理多维数组,该对象是一个快速而灵活的大数据容器。
相对于直接使用 Python,NumPy 具有一下优势:
对于同样的数值计算任务,使用 NumPy 要比直接编写 Python
代码便捷得多;
NumPy 中的数组的存储效率和输入输出性能均远远优于 Python
中等价的基本数据结构,且其能够
提升的性能是与数组中的元素成比例的;
NumPy 的大部分代码都是用 C
语言写的,其底层算法在设计时就有着优异的性能,这使得 NumPy 比纯 Python
代码高效得多.
说那么多我们不如直接来一次对比显得更直接一点,让我们来计算100000000个数字的加法运算。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| import random
import time
import numpy as np
a = []
for i in range(100000000):
a.append(random.random())
t1 = time.time()
sum_py = sum(a)
t2 = time.time()
b = np.array(a)
t4 = time.time()
sum_np = np.sum(b)
t5 = time.time()
print(f'Python:{t2-t1}, NumPy:{t5-t4}')
---
Python:1.782839059829712, NumPy:0.2144303321838379
|
在以上代码中,t2-t1 为使用 python 自带的求和函数消耗的时间,t5-t4
为使用 numpy
求和消耗的时间。我们看到了时间对比,是不是为NumPy效率的提升感到惊讶?实际上,在一些更早一些配置差一点的电脑上,这个差距还会更大。记得我以前曾经做过一样的事情,时间大概为Python: 5s, NumPy:0.5s。差了有
10
倍左右。那么我们也能看出来了,ndarray的计算速度快了很多,为我们节约了大量时间。
ndarray 对象
N 维数组对象ndarray可以说是 NumPy
中最重要的一个特点了,它是一个系列同类型数据的集合,以 0
下标为开始进行集合中元素的索引。ndarray对象是用于存放同类型元素的多维数组。
让我尝试创建一些一维数组,Numpy创建数组有三种不同的方式,1.
直接传入列表的方式; 2. 传入 range 生成序列; 3.
直接使用np.arange()生成数组。让我们一一来实现下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
list1 = [1, 2, 3, 4]
oneArray = np.array(list1)
print()
print(f'oneArray: {oneArray, type(oneArray)}')
t1 = np.array([1, 2, 3, 4])
print(f't1: {t1, type(t1)}')
t2 = np.array(range(10))
print(f't2: {t2, type(t2)}')
t3 = np.arange(0, 10, 2)
print(f't3: {t3, type(t3)}')
---
oneArray: (array([1, 2, 3, 4]), <class 'numpy.ndarray'>)
t1: (array([1, 2, 3, 4]), <class 'numpy.ndarray'>)
t2: (array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]), <class 'numpy.ndarray'>)
t3: (array([0, 2, 4, 6, 8]), <class 'numpy.ndarray'>)
|
无论用哪种方式,我们可以看到最终打印的类型都是numpy.ndarray。
那以上是一维数组的创建,我们再来看看二维数组:
1
2
3
4
5
6
7
8
9
|
list2 = [[1,2],[3,4],[5,6]]
twoArray = np.array(list2)
print(twoArray)
---
[[1 2]
[3 4]
[5 6]]
|
对于二位数组的理解,我们可以将其看成行跟列。如果是在 Excel
中,那么1,2就是一行,3,4是一行,5,6是一行。而[1,3,5]就是一列,[2,4,6]也是一列。
那么,我们在看到数据之前怎么知道这组数据的维度呢?可以使用方法ndim,
顺便,我们来学习一下一些常用属性。
1
2
3
4
5
6
7
8
9
10
11
12
13
|
print(twoArray.ndim)
print(twoArray.shape)
print(twoArray.size)
---
2
(3, 2)
6
|
这样,我们就可以看到数组的一些相关属性,拿来在处理数据前做参考。其中,获取到的shape是一个元组数据,而我们获取到的size可以看成是元组内的数据相乘。
现在我们来看,我们能否在 numpy
中调整数组的形状呢?来,尝试一下,当前我们有一组二维数组:
将其转变为ndarray并赋值给一个变量arr_1,
既然我们前面知道获取数据的形状是用shape,
那我们尝试直接更改它的shape看看是否可行:
1
2
3
4
5
6
7
8
| arr_1 = np.array([[1,2,3],[4,5,6]])
arr_1.shape = (3, 2)
print(arr_1)
---
[[1 2]
[3 4]
[5 6]]
|
居然可以。
不过虽然这样能够对数组形状进行修改,不过在 NumPy
中正确的修改方式应该是使用reshape:
1
2
3
4
5
6
7
8
9
|
arr_1 = arr_1.reshape(arr_1.shape)
print(f'\narr_1:\n{arr_1}')
---
arr_1:
[[1 2]
[3 4]
[5 6]]
|
这次我们使用了数组第一次修改后的形状,所以整个和之前没有差别,让我们再试试其他的:
1
2
3
4
5
6
7
8
9
10
11
12
|
arr_2 = arr_1.reshape((arr_1.size), order='F')
print(f'\narr_2:\n{arr_2}')
arr_3 = arr_1.flatten(order='F')
print(f'\narr_3:\n{arr_3}')
---
arr_2:
[1 3 5 2 4 6]
arr_3:
[1 3 5 2 4 6]
|
后方那个形参order是一个可选参数,是读取元素的索引顺序,有C, F, A三个固定值。C为行有限,F为列有限,
A为按数据存储顺序。
如果只是转为一维数组,使用reshape还需要知道数组的元素个数,不如flatten来的方便。这是一个专门用于将数组折叠成一维数组的方法。
让我们来看看reshape转换数组形状的其他几个例子:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
t = np.arange(24)
print(f't:\n{t}')
print(t.shape)
t1 = t.reshape((4,6))
print(f'\nt1:\n{t1}')
print(t1.shape)
t2 = t1.reshape((2, 3, 4))
print(f'\nt2:\n{t2}')
print(t2.shape)
---
t:
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
(24,)
t1:
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]
[12 13 14 15 16 17]
[18 19 20 21 22 23]]
(4, 6)
t2:
[[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[[12 13 14 15]
[16 17 18 19][9, 12, 88, 14, 25] <class 'list'>
[20 21 22 23]]]
(2, 3, 4)
|
在数据转为了ndarray之后,方便了我们在NumPy中进行计算等操作,不过很多时候,最终我们还是要转回
Python 内的
List。如果需要进行转换,直接使用tolist()就可以了。
1
2
3
4
5
6
7
|
a = np.array([9, 12, 88, 14, 25])
items = a.tolist()
print(items, type(items))
---
[9, 12, 88, 14, 25] <class 'list'>
|
NumPy 的数据类型
在之前的 Python 基础课程中,我用几节课给大家讲了一遍 Python
中的数据类型。同样的,在 NumPy
中也有一些不同的数据类型,大多数时候,他们都可以进行转换。
来直接上代码看几个例子:
1
| arr = np.array([1, 2, 3, 4, 5], dtype=np.int16)
|
这样,我们就在 Numpy
中生成了一个int16类型的数组。我们来看看这组数据的元素长度和类型:
1
2
3
4
5
6
7
8
|
print(arr.itemsize)
print(arr.dtype)
---
2
int16
|
当然,就如我们之前说的,数据的类型之间是可以进行转换的,转换也十分方便,直接使用类型方法就可以了。
1
2
3
4
5
6
|
arr_2 = arr.astype(np.int64)
print(arr_2.dtype)
---
int64
|
这里给大家多讲一个小技巧,让我们看看如何生成随机小数:
1
2
3
4
5
6
7
8
9
|
print(round(random.random(), 2))
arr_3 = np.round([random.random() for i in range(10)],2)
print(arr_3)
---
0.47
[0.97 0.81 0.1 0.23 0.66 0.98 0.06 0.44 0.33 0.14]
|
既然我们知道了dtype是numpy中的数据类型,那么对于数组来说,都有哪些类型呢?这里给大家一个表:
np.bool |
用一个字节存储的布尔类型(True 或 False) |
'b' |
np.int8 |
一个字节大小,-128 至 127 (一个字节) |
'i' |
np.int16 |
整数,-32768 至 32767 (2 个字节) |
'i2' |
np.int32 |
整数,-2 31 至 2
32 -1 (4 个字节) |
'i4' |
np.int64 |
整数,-2 63 至 2
63 - 1 (8 个字节) |
'i8' |
np.uint8 |
无符号整数,0 至 255 |
'u' |
np.uint16 |
无符号整数,0 至 65535 |
'u2' |
np.uint32 |
无符号整数,0 至 2 ** 32 - 1 |
'u4' |
np.uint64 |
无符号整数,0 至 2 ** 64 - 1 |
'u8' |
np.float16 |
半精度浮点数:16 位,正负号 1 位,指数 5 位,精度 10 位 |
'f2' |
np.float32 |
单精度浮点数:32 位,正负号 1 位,指数 8 位,精度 23 位 |
'f4' |
np.float64 |
双精度浮点数:64 位,正负号 1 位,指数 11 位,精度 52 位 |
'f8' |
np.complex64 |
复数,分别用两个 32 位浮点数表示实部和虚部 |
'c8' |
np.complex128 |
复数,分别用两个 64 位浮点数表示实部和虚部 |
'c16' |
np.object_ |
python 对象 |
'O' |
np.string_ |
字符串 |
'S' |
np.unicode_ |
unicode 类型 |
'U' |
数组的计算
numpy
的广播机制在运算过程中,加减乘除的值被广播到所有的元素上面:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| t1 = np.arange(24).reshape((6,4))
print('原数组:\n', t1)
print('加 2:\n', t1+2)
print('乘 2:\n', t1*2)
print('除 2:\n', t1/2)
---
原数组:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]
加 2:
[[ 2 3 4 5]
[ 6 7 8 9]
[10 11 12 13]
[14 15 16 17]
[18 19 20 21]
[22 23 24 25]]
乘 2:
[[ 0 2 4 6]
[ 8 10 12 14]
[16 18 20 22]
[24 26 28 30]
[32 34 36 38]
[40 42 44 46]]
除 2:
[[ 0. 0.5 1. 1.5]
[ 2. 2.5 3. 3.5]
[ 4. 4.5 5. 5.5]
[ 6. 6.5 7. 7.5]
[ 8. 8.5 9. 9.5]
[10. 10.5 11. 11.5]]
|
除了和数字进行计算之外,同种形状的数组之间也是可以进行计算(对应位置进行计算操作)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| t1 = np.arange(24).reshape(6,4)
t2 = np.arange(100, 124).reshape(6,4)
print('相加:\n',t1+t2)
print('相乘:\n',t1*t2)
---
相加:
[[100 102 104 106]
[108 110 112 114]
[116 118 120 122]
[124 126 128 130]
[132 134 136 138]
[140 142 144 146]]
相乘:
[[ 0 101 204 309]
[ 416 525 636 749]
[ 864 981 1100 1221]
[1344 1469 1596 1725]
[1856 1989 2124 2261]
[2400 2541 2684 2829]]
|
那么,不同形状的多维数组能否可以计算呢?来,一起试试看:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| t1 = np.arange(24).reshape((4,6))
t2 = np.arange(18).reshape((3,6))
print(t1)
print(t2)
print(t1-t2)
---
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]
[12 13 14 15 16 17]
[18 19 20 21 22 23]]
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]
[12 13 14 15 16 17]]
ValueError: operands could not be broadcast together with shapes (4,6) (3,6)
|
做相加操作的时候报错了,所以我们平时在处理数据的时候一定要多注意这种情况发生。不同形状的多维数组是不能进行计算的。
我们继续来往后做实验看看,行数或者列数相同的一维数组和多维数组可以进行计算吗?
先看看行形状相同的情况:
1
2
3
4
5
6
7
8
9
| t1 = np.arange(24).reshape(4,6)
t2 = np.arange(0, 6)
print(t1 - t2)
---
[[ 0 0 0 0 0 0]
[ 6 6 6 6 6 6]
[12 12 12 12 12 12]
[18 18 18 18 18 18]]
|
看到结果我们就明白了,多维数组中的每一行数组都分别和一维数组中的数据进行操作,也就是会与每一行数组的对应位相操作。
那么列形状相同是否也是相同情况?
1
2
3
4
5
6
7
8
9
| t1 = np.arange(24).reshape(4,6)
t2 = np.arange(4).reshape(4,1)
print(t1-t2)
---
[[ 0 1 2 3 4 5]
[ 5 6 7 8 9 10]
[10 11 12 13 14 15]
[15 16 17 18 19 20]]
|
就跟预料的一样,每一列的数组的对应位都进行了操作。
数组的轴
在理解了一维数组和二维数组之后,我们来看看数组中的轴。
什么是轴?在 Numpy 中,我们可以讲轴理解为方向,使用 0,1,2
数字来表示,对于一个一维数组,只有一个 0
轴。二维数组(shape(2,2))呢,就有 0 轴和 1
轴,那同理向上推断,三维数组(shape(2,2,3))会有 0,1,2 三个轴。
那么我们到底为什么要了解和学习轴呢?有了轴的概念之后,我们计算讲会更加方便,比如计算一个二维数组的平均值,必须制定是计算哪个方向上面的数字的平均值。
下图中,我列出了不同数组的轴,看着图相信会好理解很多:
一维数组:

二维数组:
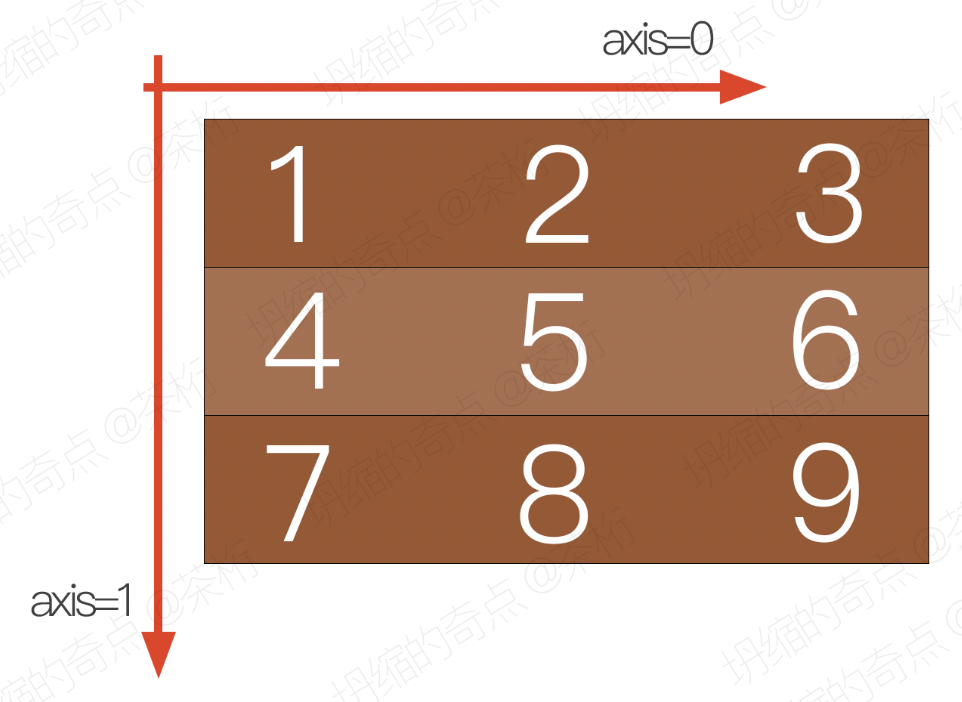
三维数组:

看完图之后,让我们再放到代码里去理解一下轴的概念,我们先创建一个二维数组,然后用数组内的数据分别从
0 轴和 1 轴进行相加计算总和,得出的结果如下:
1
2
3
4
5
6
7
| a = np.array([[1,2,3], [4,5,6]])
print(np.sum(a, axis=0))
print(np.sum(a, axis=1))
---
[5 7 9]
[ 6 15]
|
也就是说,我们按 0
轴算总和的时候,是列相加(1+4,2+5,3+6),我们按 1
轴相加算总和的时候,是行相加(1+2+3, 4+5+6)
再让我们看看后面形参上我们不给行列值,计算的总和会是多少?
1
2
3
4
| print(np.sum(a))
---
21
|
也就是这个数组内的所有数字相加得到的结果。
在理解了二维数组行列相加的不同之后,我们再来看看三维数组,让我们先创建一个三维数组:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| a = np.arange(27).reshape(3,3,3)
print(a)
---
[[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]]
[[ 9 10 11]
[12 13 14]
[15 16 17]]
[[18 19 20]
[21 22 23]
[24 25 26]]]
|
接着,我们来分别按不同数轴进行计算来看看:
1
2
3
4
5
6
7
|
print(np.sum(a, axis=0))
---
[[27 30 33]
[36 39 42]
[45 48 51]]
|
1
2
3
4
5
6
7
|
print(np.sum(a, axis=1))
---
[[ 9 12 15]
[36 39 42]
[63 66 69]]
|
1
2
3
4
5
6
7
|
print(np.sum(a, axis=2))
---
[[ 3 12 21]
[30 39 48]
[57 66 75]]
|
虽然最后相加之后得到的都是 3X3
的二维数组,但是计算结果大相径庭。我们就不一一分析,只拿计算结果的第一个数字来看,就能明白,其他数字都是一样的计算方法:
axis=0,
第一行的第一个数字得到过程为:0+9+18;
axis=1, 第一行的第一个数字得到的过程为:
0+3+6;
axis=2,
第一行的第一个数字得到的过程为:0+1+2;
那现在,我们是不是对于轴相加的计算过程就比较理解了?
最后总结一下,在计算的时候可以想象成是每一个坐标轴,分别计算这个轴上面的每一个刻度上的值,或者在二维数组中记住
0 表示列 1 表示行。
索引和切片
在学习 Python 基础课程的时候,我们应该已经了解过索引和切片的概念,在
Numpy
数组中这个概念也并无不同,一样也是开始值,结束值,步进值(start:stop:step)来进行切片操作。
1
2
3
4
5
| a = np.arange(10)
print(a[2:7:2])
---
[2 4 6]
|
我们创建了一个一维数组,然后从索引 2 开始到索引 7 停止,间隔为
2。
和 Python
中的下标索引方式相同,在这个以为数组中,我们使用[2]一样可以获取到下标为
2 的那个元素:
1
2
3
4
| print(a[2], a)
---
2 [0 1 2 3 4 5 6 7 8 9]
|
还记得[2:]代表的含义吗?不太记得的话,我们来看看在 Numpy
的数组中操作会怎么样,其结果和 Python 对列表进行操作一样:
1
2
3
4
| print(a[2:])
---
[2 3 4 5 6 7 8 9]
|
那以上这些操作我们都是对一维数组进行操作,大家可能还相对比较好理解。因为我们可以将其代入成一个
Python 列表,那对列表进行索引和切片的操作我们之前已经学过。
可是如果是多维数组进行操作,又和一维数组有什么不同呢?我们先来创建一个
4 行 6 列的二维数组:
1
2
3
4
5
6
7
8
| t1 = np.arange(24).reshape(4,6)
print(t1)
---
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]
[12 13 14 15 16 17]
[18 19 20 21 22 23]]
|
然后我们现在来一样对其使用[2]来进行操作:
1
2
3
4
| print(t1[2])
---
[12 13 14 15 16 17]
|
是不是和一维数组不太一样?在t1数组中,我们打印的数据应该是它按行往下数第
3 行,那其实就是行下标的 2,
按行数从上往下数的下标分别为[0, 1, 2]
那么我们如果使用切片的话,以这种方式去思考,应该是从当前下标的行往后取,对吧?对不对我们直接来试试就知道了:
1
2
3
4
5
| print(t1[2:])
---
[[12 13 14 15 16 17]
[18 19 20 21 22 23]]
|
这是从当前行开始向下连续取多行。
那如果是取中间的连续部分呢?
1
2
3
4
5
| print(t1[1:3])
---
[[ 6 7 8 9 10 11]
[12 13 14 15 16 17]]
|
这样,我们就取到了第二和第三行。
有的时候,我们可能需要隔行取值:
1
2
3
4
5
6
| print(t1[[0,2,3]])
---
[[ 0 1 2 3 4 5]
[12 13 14 15 16 17]
[18 19 20 21 22 23]]
|
我们现在是知道了如何按行来获取数组中的数据,同样,我们还可以按列来获取。
在学习如何按列获取数据之前,我们先来看看如何获取到某行某列的那单个数据:
这样,表示的意思就是第二行第三列,我们如愿取到了 15 这个值。
而从这种方式我们基本就可以看的出来,在获取数据的时候,我们用到了[axis1,axis0]这样的形式去准确的定位。知道了这个,就简单了。
既然,号之前的数值代表行下标,那,之后的数值应该就是列下标。一样,从
0
开始。和取行不同的地方在于,我们在取行的时候可以在,号之后加:这个符号来表示所有列,当然也可以不加,这是一种默认的方式。而取列的时候,我们必须在前面加上行的下标,如果是全取值,得加上:。
比方说,我们之前按行取值的时候:
1
2
| print(t1[1:3])
print(t1[1:3,:])
|
这两种方式实际上是一样的。因为默认方式列上
:的取值方式。
就如我们刚才说到的,按列取值的时候,行就必须加上:才行。
1
2
3
4
| print(t1[,2])
---
SyntaxError: invalid syntax
|
看,报错了。我们只有在前面将取所有行加上才行,又或者加上某一行的值:
1
2
3
4
| print(t1[:,2])
---
[ 2 8 14 20]
|
这样,我们就取到了第三列的值。
和取行一样,列也可以连续取值:
1
2
3
4
5
6
7
| print(t1[:, 2:])
---
[[ 2 3 4 5]
[ 8 9 10 11]
[14 15 16 17]
[20 21 22 23]]
|
我们如愿从第三列开始向后连续取值。
那如果是不连续的呢?也和行是一样的形式:
1
2
3
4
5
6
7
| print(t1[:,[0,2,3]])
---
[[ 0 2 3]
[ 6 8 9]
[12 14 15]
[18 20 21]]
|
有没有发现,当我们了解了行列关系和取值方式代表的意义之后,那这个多维数组就任我们拿捏了。其原理显得非常简单。
好,让我们多加一个难度稍微高一点的取值,我们需要从行,从列都取不连续的值。那还不简单,不就是[[行,行,行...],[列,列,列...]]的方式吗。
1
2
3
4
| print(t1[[0,1,1],[0,1,3]])
---
[0 7 9]
|
这,其实就是一种定点取值的方式了。
修改数组的值
在了解完如何进行查询查找之后,我们现在在来学习一下如何对其中的值进行修改。在平时我们处理数据的时候,替换修改数值是常有的事情,我们每次修改之后,都会将之前的值复原。
我们从修改行的值开始,因为这个比较好理解:
1
2
3
4
5
6
7
8
9
|
t1[1] = 0
print(t1)
---
[[ 0 1 2 3 4 5]
[ 0 0 0 0 0 0]
[12 13 14 15 16 17]
[18 19 20 21 22 23]]
|
就是如此简单,定位好数值后,直接用=赋值就可以了。
那同理,修改某一列的数据也是如此操作。
1
2
3
4
5
6
7
8
9
| t1 = np.arange(24).reshape(4,6)
t1[:,1] = 0
print(t1)
---
[[ 0 0 2 3 4 5]
[ 6 0 8 9 10 11]
[12 0 14 15 16 17]
[18 0 20 21 22 23]]
|
修改连续多行和修改连续多列的方式也是一样,这次让我们来一次联动操作,将其中的连续多行多列一起修改掉:
1
2
3
4
5
6
7
8
9
| t1 = np.arange(24).reshape(4,6)
t1[1:3,1:4] = 0
print(t1)
---
[[ 0 1 2 3 4 5]
[ 6 0 0 0 10 11]
[12 0 0 0 16 17]
[18 19 20 21 22 23]]
|
当然,既然可以连续多行多列进行修改,那我们肯定也能够进行定点修改值
1
2
3
4
5
6
7
8
9
| t1 = np.arange(24).reshape(4,6)
t1[[0,1],[0,3]] = 0
print(t1)
---
[[ 0 1 2 3 4 5]
[ 6 7 8 0 10 11]
[12 13 14 15 16 17]
[18 19 20 21 22 23]]
|
那基本上,如何按照行列寻找值并修改也就这么多内容,大家多操作完全可以轻易掌握。
别着急,还没结束,按行按列并不能完全满足我们平时的要求,有的时候,我们是要对数值按条件进行修改的。打个比方说,我们需要对所有大于
2 小于 12
的值进行修改,那么这又该如何实现?总不会在数组中可以用比较运算符来判断吧?嗯,没错,就是要用比较运算符符来判断,完全可以:
1
2
3
4
5
| t1 = np.arange(24).reshape(4,6)
t1[2<t1 and t1<12] = 0
---
ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()
|
报错了,怎么回事,不是说好的可以用比较运算符判断吗?
原因其实就是,我们不能使用and,or这样的方式,我们来改变一下逻辑运算符的方式:
1
2
3
4
5
6
7
8
9
| t1 = np.arange(24).reshape(4,6)
t1[(2<t1)&(t1<12)] = 0
print(t1)
---
[[ 0 1 2 0 0 0]
[ 0 0 0 0 0 0]
[12 13 14 15 16 17]
[18 19 20 21 22 23]]
|
成功了,从 3 到 11 我们全部替换成了 0。
其实,在 NumPy
中,也有相应的方法名来替代&, |, ~这种逻辑运算符,我们来看:
1
2
3
4
5
6
7
8
9
| t1 = np.arange(24).reshape(4,6)
t1[(np.logical_and(t1>2, t1<12))] = 0
print(t1)
---
[[ 0 1 2 0 0 0]
[ 0 0 0 0 0 0]
[12 13 14 15 16 17]
[18 19 20 21 22 23]]
|
这就是在 NumPy
中特殊的逻辑运算方法。「与、或、非」对应的方法如下:
np.logical_and: 与&np.logical_or: 或|np.logical_not: 非~
大家可以依次去试试,我这里另外给大家拓展一个方式,就是三目运算方式,这种方式在今后的数据处理中,我们会经常看到,其形式为:
1
| 三目运算 np.where(condition, x, y),满足条件(condition)输出 x, 不满足输出 y
|
我们来看个例子:
1
2
3
4
5
6
7
8
| score = np.array([[80,88],[82,81],[75,81]])
result = np.where(score>80, True, False)
print(result)
---
[[False True]
[ True True]
[False True]]
|
在我们平时处理数据的过程当中,数据并不是如此完美,除了修改之外,更多的时候是需要我们去添加、删除以及去重。接下来,就让我们看看这部分该如何操作:
数组的添加
numpy.append函数在数组的末尾添加值。
追加操作会分配整个数组,并把原来的数组复制到新数组中。
此外,输入数组的维度必须匹配否则将生成 ValueError。
在其中的参数意义如下:
arr: 输入数组
values:要向 arr 添加的值,需要和 arr
形状相同(除了要添加的轴)。
axis:默认为 None。当 axis
无定义时,是横向加成,返回总是为一维数组!当 axis 有定义的时候,分别为 0
和 1 的时候。当 axis 有定义的时候,分别为 0 和 1
的时候(列数要相同)。当 axis 为 1
时,数组是加在右边(行数要相同)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
a = np.array([[1,2,3], [4,5,6]])
print(f'第一个数组:\n{a}\n')
print(f'向数组添加元素:\n{np.append(a, [7,8,9])}\n')
print(f'沿轴 0 添加元素:\n{np.append(a, [[7,8,9]], axis=0)}\n')
print(f'沿轴 1 添加元素:\n{np.append(a, [[5,5,5],[7,8,9]], axis=1)}\n')
---
第一个数组:
[[1 2 3]
[4 5 6]]
向数组添加元素:
[1 2 3 4 5 6 7 8 9]
沿轴 0 添加元素:
[[1 2 3]
[4 5 6]
[7 8 9]]
沿轴 1 添加元素:
[[1 2 3 5 5 5]
[4 5 6 7 8 9]]
|
除了append之外,我们还可以使用insert进行添加。
numpy.insert:函数在给定索引之前,沿给定轴在输入数组中插入值。如果值的类型转换为要插入,则它与输入数组不同。
插入没有原地的,函数会返回一个新数组。
此外,如果未提供轴,则输入数组会被展开。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| a = np.array([[1,2],[3,4],[5,6]])
print(f'第一个数组:\n{a}\n')
print(f'未传递 Axis 参数,在插入之前输入数组会被展开:\n{np.insert(a,3,[11,12])}\n')
print('\n 传递了 Axis 参数,会广播值数组来配输入数组')
print(f'沿轴 0 广播:\n{np.insert(a,1,[11], axis=0)}\n')
print(f'沿轴 1 广播:\n{np.insert(a,1,11, axis=1)}\n')
---
第一个数组:
[[1 2]
[3 4]
[5 6]]
未传递 Axis 参数,在插入之前输入数组会被展开:
[ 1 2 3 11 12 4 5 6]
传递了 Axis 参数,会广播值数组来配输入数组
沿轴 0 广播:
[[ 1 2]
[11 11]
[ 3 4]
[ 5 6]]
沿轴 1 广播:
[[ 1 11 2]
[ 3 11 4]
[ 5 11 6]]
|
从代码中我们可以看出来,insert相比较而言在arr和values之间多了一个形参,用于指示插入数据的下标位置。
接着,我们来看看如何在数组中操作删除。
npmpy.delete:
函数返回从输入数组中删除指定子数组的新数组。 与
insert()函数的情况一样,如果未提供轴参数,则输入数组将展开。
参数说明:
arr:输入数组
obj:可以被切片,整数或者整数数组,表明要从输入数组删除的子数组
axis:沿着它删除给定子数组的轴,如果未提供,则输入数组会被展开。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| a = np.arange(12).reshape(3,4)
print(f'第一个数组:\n{a}\n')
print(f'未传递 Axis 参数。在删除之前输入数组会被展开:\n{np.delete(a, 5)}\n')
print(f'删除每一行中的第二列:\n{np.delete(a,1,axis=1)}\n')
---
第一个数组:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
未传递 Axis 参数。在删除之前输入数组会被展开:
[ 0 1 2 3 4 6 7 8 9 10 11]
删除每一行中的第二列:
[[ 0 2 3]
[ 4 6 7]
[ 8 10 11]]
|
接下来,估计是我们清洗数据最常用到的操作,就是「去重」。
numpy.unique: 函数用于去除数组中的重复元素。
参数说明:
arr:输入数组,如果不是一维数组则会展开.
return_index:如果为
true,返回新列表元素在旧列表中的位置(下标),并以列表形式储.
return_inverse:如果为
true,返回旧列表元素在新列表中的位置(下标),并以列表形式储 .
return_counts:如果为
true,返回去重数组中的元素在原数组中的出现次数.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| a = np.array([5,2,6,2,7,5,6,7,2,9])
print(f'第一个数组:\n{a}\n')
print(f'第一个数组的去重值:\n{np.unique(a)}\n')
print('去重数组对应原数组的索引下标数组:')
u,indices = np.unique(a, return_index = True)
print(indices)
print('\n 我们可以看到每个和原数组下标对应的数值:')
print(u)
print('\n 原数组对应去重数组的下标数组:')
u,indices = np.unique(a, return_inverse = True)
print(u)
print(indices)
print ('\n 返回去重元素的重复数量:')
u,indices = np.unique(a,return_counts = True)
print (u)
print (indices)
---
第一个数组:
[5 2 6 2 7 5 6 7 2 9]
第一个数组的去重值:
[2 5 6 7 9]
去重数组对应原数组的索引下标数组:
[1 0 2 4 9]
我们可以看到每个和原数组下标对应的数值:
[2 5 6 7 9]
原数组对应去重数组的下标数组:
[2 5 6 7 9]
[1 0 2 0 3 1 2 3 0 4]
返回去重元素的重复数量:
[2 5 6 7 9]
[3 2 2 2 1]
|
我用图形来解释一下「第一个数组的去重值」和「去重数组的索引数组」,至于其他的,也是类似的分析方式。

在去重的方法中,我们都有两个变量去接收返回值,也就是方法返回了两个值,其中u这个变量就代表的是改变之后的数组,而indices则是重新组成的数组中的数值在原数组中第一次出现的下标位置,又或者是出现次数。以方法不同,但是u肯定是去重后的重新组成的数组。
我标识了一下原数组中的下标,并且用颜色区分了一下。在重新组成的去重的数组中,可以看到已经没有重复的数值了,然后对比原数组,每一个不重复的数值也都还在。而默认的排序方式就是从小到大的排序。所以重新组成的数值中的排序和原数组中不太一样。
然后我们再来看最下面「去重下标」部分,虽然这也是一个数组,但是实际上它是一个完全由下标位置组成的数组,然后我们来看去重数组,我们是拿第一次出现的下标来算。其中2对应原数组就的下标就是1,
5第一次出现是0的位置,6是2,
7是4,9这是最后一位,也就是下标9。
所以对重新组成的数组稍微一分析,就能明白每个方法的返回值说代表的意义。
相信到这里,大家应该也都能理解了。
接下来,我们要来看看重头戏,NumPy 的计算。
NumPy 的计算
NumPy 原本就是一个科学计算的第三方库,所以计算能力应该算是 NumPy
里的重点。在原始方法中,有许许多多的方法用于数据的计算。包括求最大值,求最小值,平均值,累计和等等。除了计算整体之外,还支持在不同轴上进行计算。下面我们来看看,NumPy
到底为我们都提供了哪些好用的方法,最开始,还是让我们来生成一组新的数据:
1
2
3
4
5
6
7
| score = np.array([[80,88],[82,81],[75,81]])
score
---
array([[80, 88],
[82, 81],
[75, 81]])
|
获取所有数据最大值
1
2
3
4
5
| result = np.max(score)
print(result)
---
88
|
获取某一个轴上的数据最大值
1
2
3
4
5
| result = np.max(score,axis=0)
print(result)
---
[82 88]
|
获取最小值
1
2
3
4
5
| result = np.min(score)
print(result)
---
75
|
获取某一个轴上的数据最小值
1
2
3
4
5
| result = np.min(score,axis=1)
print(result)
---
[80 81 75]
|
数据的比较
第一个参数中的每一个数与第二个参数比较返回大的
1
2
3
4
5
| result = np.maximum([-2, -1, 0, 1, 2], 0)
print(result)
---
[0 0 0 1 2]
|
第一个参数中的每一个数与第二个参数比较返回小的
1
2
3
4
5
| result = np.minimum([-2, -1, 0, 1, 2], 0)
print(result)
---
[-2 -1 0 0 0]
|
以上两组代码中,当方法内接受两个参数,当然也可以大小一致;
当第二个参数只是一个单独的值时,其实是用到了维度的广播机制。如果第二个参数是一个同样长度的数组,会分别比较不同位置。
1
2
3
4
5
| result = np.maximum([-2, -1, 0, 1, 2], [1,2,3,4,5])
print(result)
---
[1 2 3 4 5]
|
咱们在这里稍微讲一下 NumPy
中的广播机制,其实是有点晦涩难懂。大家尝试理解一下看看。
广播机制是 Numpy 让两个不同 shape
的数组能够做一些运算,需要对参与运算的两个数组做一些处理或者说扩展,最终是参与运算的两个数组的
shape 一样,然后广播计算(对应位置数据进行某运算)得到结果。
以我们做数据比较的第一组为例,当我们去对比第一个参数和第二个参数返回大的,这个时候我们给到的两个参数分别是:
[-2,-1,0,1,2]和0,但是由于广播机制的存在,在NumPy中实际上是这么处理的,第一个参数还是[-2,-1,0,1,2],
而第二个参数实际上是[0,0,0,0,0]。
获取所有数据的平均值
1
2
3
4
5
| result = np.mean(score)
print(result)
---
81.16666666666667
|
获取某一行或一列的平均值
1
2
3
4
5
| result = np.mean(score, axis=0)
print(result)
---
[79. 83.33333333]
|
返回给定axis上的累计和
1
2
3
4
5
6
7
8
9
| t1 = np.array([[1,2,3],[4,5,6]])
print(t1)
print(t1.cumsum(0))
---
[[1 2 3]
[4 5 6]]
[[1 2 3]
[5 7 9]]
|
在来看值为axis=1时:
1
2
3
4
5
| print(t1.cumsum(1))
---
[[ 1 3 6]
[ 4 9 15]]
|
我们可以这样认为,当cumsum(0),也就是axis=0时,是这样计算的:
1
2
| [1 2 3] --------> |1 |2 |3 |
[5 7 9] --------> |5=1+4 |7=2+5 |9=3+6|
|
当cumsum(1),也就是axis=1时,是这样计算的:
1
2
| [ 1 3 6] ------> |1 |3=2+1 |6=3+2+1 |
[ 4 9 15] ------> |4 |9=4+5 |15=4+5+6 |
|
argmin求最小值索引
1
2
3
4
5
| result = np.argmin(score, axis=0)
print(result)
---
[2 1]
|
我们看score这组数据中,75是第一列最小值,81是第二列最小值。当然,第二列的数据中有两个81。现在让我们讲数组的值换一下看看:
1
2
3
4
5
6
| score[2,1] = 64
result = np.argmin(score, axis=0)
print(result)
---
[2 2]
|
很显然,我们第二列的最小值变成了64,
在那一列中,它的坐标为2。
求每一列的标准差
标准差是一组数据平均值分散程度的一种度量。一个较大的标准差,代表大部分数值和其平均值之间差异较大;一个较小的标准差,代表这些数据较接近平均值反应出数据的波动稳定情况,越大表示波动越大,越不稳定。
1
2
3
4
5
| result = np.std(score, axis=0)
print(result)
---
[ 2.94392029 10.07747764]
|
从结果中可以看出来,我们第二列的波动较大。其原因正是因为我把[2,2]这个位置的值替换成了64。和其他值拉大了差距。
极值
1
2
3
4
5
| result = np.ptp(score,axis=None)
print(result)
---
24
|
计算极值,其实也就是最大值和最小值的差。在score中,最大值为88,最小值为64。
除了我们目前测试的这些方法之外,NumPy
中还有很多其他方法。比如,计算反差的var,
协方差cov,平均值average,
中位数median。在这里,我们就不一一测试了,方法都比较简单,拿来直接用的那种。
我将通用函数和解释在这里列一个表:
| numpy.sqrt(array) |
平方根函数 |
| numpy.exp(array) |
e^array[i]的数组 |
| numpy.abs/fabs(array) |
计算绝对值 |
| numpy.square(array) |
计算各元素的平方 等于 array**2 |
| numpy.log/log10/log2(array) |
计算各元素的各种对数 |
| numpy.sign(array) |
计算各元素正负号 |
| numpy.isnan(array |
计算各元素是否为 NaN |
| numpy.isinf(array) |
计算各元素是否为 NaN |
| numpy.cos/cosh/sin/sinh/tan/tanh(array) |
三角函数 |
| numpy.modf(array) |
将 array 中值得整数和小数 分离,作两个数组返回 |
| numpy.ceil(array) |
向上取整,也就是取比这个 数大的整数 |
| numpy.floor(array) |
向下取整,也就是取比这个 数小的整数 |
| numpy.rint(array) |
四舍五入 |
| numpy.trunc(array) |
向 0 取整 |
| numpy.cos(array) |
正弦值 |
| numpy.sin(array) |
余弦值 |
| numpy.tan(array) |
正切值 |
| numpy.add(array1,array2) |
元素级加法 |
| numpy.subtract(array1,array2) |
元素级减法 |
| numpy.multiply(array1,array2) |
元素级乘法 |
| numpy.divide(array1,array2) |
元素级除法 array1./array2 |
| numpy.power(array1,array2) |
元素级指数 array1.^array2 |
| numpy.maximum/minimum(array1,aray2) |
元素级最大值 |
| numpy.fmax/fmin(array1,array2) |
元素级最大值,忽略 NaN |
| numpy.mod(array1,array2) |
元素级求模 |
| numpy.copysign(array1,array2) |
将第二个数组中值得符号复 制给第一个数组中值 |
| numpy.greater/greater_equal/less/less_equal/equal/not_equal
(array1,array2) |
元素级比较运算,产生布尔 数组 |
| numpy.logical_end/logical_or/logic_xor(array1,array2) |
元素级的真值逻辑运算 |
数组的拼接
有的时候我们需要将两个数据加起来一起研究分析,我们就可以将其进行拼接然后分析。
我们先创建两组数组:
1
2
| a = np.array([[1,2],[3,4]])
b = np.array([[5,6],[7,8]])
|
然后我们现在先根据轴连接的数组序列
先沿轴 0 连接两个数组:
1
2
3
4
5
6
7
| print(np.concatenate((a,b), axis=0))
---
[[1 2]
[3 4]
[5 6]
[7 8]]
|
再沿轴 1 连接两个数组:
1
2
3
4
5
| print(np.concatenate((a,b), axis=1))
---
[[1 2 5 6]
[3 4 7 8]]
|
根据轴进行堆叠
沿轴 0 堆叠两个数组:
1
2
3
4
5
6
7
8
| print(np.stack((a,b), axis=0))
---
[[[1 2]
[3 4]]
[[5 6]
[7 8]]]
|
沿轴 1 堆叠两个数组:
1
2
3
4
5
6
7
8
| print(np.stack((a,b), axis=1))
---
[[[1 2]
[5 6]]
[[3 4]
[7 8]]]
|
矩阵垂直拼接
1
2
3
4
5
6
7
8
9
10
| v1 = [[0,1,2,3,4,5], [6,7,8,9,10,11]]
v2 = [[12,13,14,15,16,17],[18,19,20,21,22,23]]
result = np.vstack((v1, v2))
print(result)
---
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]
[12 13 14 15 16 17]
[18 19 20 21 22 23]]
|
矩阵水平拼接
1
2
3
4
5
6
| result = np.hstack((v1, v2))
print(result)
---
[[ 0 1 2 3 4 5 12 13 14 15 16 17]
[ 6 7 8 9 10 11 18 19 20 21 22 23]]
|
数组的分割
将一个数组分割为多个子数组
参数说明:
ary:被分割的数组
indices_or_sections:果是一个整数,就用该数平均切分,如果是一个数组,为沿轴切分的位置(左开右
闭)
axis:沿着哪个维度进行切向,默认为 0,横向切分。为 1
时,纵向切分
1
2
3
4
5
6
7
8
| arr = np.arange(9).reshape(3,3)
print('将数组分成三个大小相等的子数组:')
b = np.split(arr,3)
print(b)
---
将数组分成三个大小相等的子数组:
[array([[0, 1, 2]]), array([[3, 4, 5]]), array([[6, 7, 8]])]
|
numpy.hsplit函数用于水平分割数组,通过指定要返回的相同形状的数组数量来拆分原数组。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| harr = np.floor(10 * np.random.random((2,6)))
print(f'原 array:\n{harr}')
print(f'\n 水平分割后:\n{np.hsplit(harr, 3)}')
---
原 array:
[[1. 1. 8. 2. 3. 9.]
[3. 1. 6. 6. 5. 6.]]
水平分割后:
[array([[1., 1.],
[3., 1.]]), array([[8., 2.],
[6., 6.]]), array([[3., 9.],
[5., 6.]])]
|
这里我们说一下floor(),
这个方法会返回数值的下舍整数(舍去小数点求整型)。
numpy.vsplit会沿垂直轴分割
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| a = np.arange(16).reshape(4,4)
print(f'第一个数组:\n{a}')
print(f'\n 垂直分割之后:\n{np.vsplit(a,2)}')
---
第一个数组:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]]
垂直分割之后:
[array([[0, 1, 2, 3],
[4, 5, 6, 7]]), array([[ 8, 9, 10, 11],
[12, 13, 14, 15]])]
|
nan和inf
C
语言中表示最大的正整数值是0x7FFFFFFF,最小的负整数是0x80000000。inf
表示无穷大,需要使用 float(‘inf’)函数来转化,那么对应的就有
float('-inf')表示无穷小了。这样你就可以使用任意数来判断和它的关系了。
那什么时候会出现inf呢?
比如一个数字除以0,Python 中会报错,但是 numpy
中会是一个inf或者-inf
另外还有
nan,这种写法在pandas中常见,表示缺失的数据,所以一般用nan来表示。任何与其做运算结果都是nan。
1
2
3
4
5
6
7
8
| a = np.nan
b = np.inf
print(a, type(a))
print(b, type(b))
---
nan <class 'float'>
inf <class 'float'>
|
判断数组中为nan的个数(注意:float
类型的数据才能赋值nan)
1
| t = np.arange(24,dtype=float).reshape(4,6)
|
可以使用np.count_nonzero()来判断非零的个数
1
2
3
4
| print(np.count_nonzero(t))
---
23
|
将三行四列的数改成 nan
1
2
3
4
5
| t[3,4] = np.nan
print(t[3,4] != np.nan)
---
True
|
注意到没有,np.nan != np.nan居然是True。难道我们更改数据失败了?我们打出来看看:
1
2
3
4
5
6
7
| print(t)
---
[[ 0. 1. 2. 3. 4. 5.]
[ 6. 7. 8. 9. 10. 11.]
[12. 13. 14. 15. 16. 17.]
[18. 19. 20. 21. nan 23.]]
|
没错,t[3,4]确实被改变了,那只能说明np.nan != np.nan是确实存在的。
所以,我们就可以使用这两个结合使用判断nan的个数:
1
2
3
4
| print(np.count_nonzero(t != t))
---
1
|
我们之前讲过,nan和任何数计算都为nan
1
2
3
4
| print(np.sum(t,axis=0))
---
[36. 40. 44. 48. nan 56.]
|
接下来,让我们做一个具体的练习,在练习中,我们将处理数组中的nan
1
2
3
4
5
6
7
8
9
10
11
12
|
t = np.arange(24).reshape(4,6).astype('float')
t[1, 3:] = np.nan
print(t)
---
[[ 0. 1. 2. 3. 4. 5.]
[ 6. 7. 8. nan nan nan]
[12. 13. 14. 15. 16. 17.]
[18. 19. 20. 21. 22. 23.]]
|
现在我们得到了一组包含nan的数组,接着我们来处理这组数据:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
for i in range(t.shape[1]):
temp_col = t[:, i]
nan_num = np.count_nonzero(temp_col != temp_col)
if nan_num != 0:
temp_col_not_nan = temp_col[temp_col == temp_col]
temp_col[np.isnan(temp_col)] = np.mean(temp_col_not_nan)
print(t)
---
[[ 0. 1. 2. 3. 4. 5.]
[ 6. 7. 8. 13. 14. 15.]
[12. 13. 14. 15. 16. 17.]
[18. 19. 20. 21. 22. 23.]]
|
这样,我们就处理了这组数据中的nan,至于替换成平均值填补空缺数据,这个是清洗数据的通用做法。
二维数组的转置
针对二维数组的转置,也就是对换数组的维度。说的直白一点,就是行转列,列转行。
这在处理数据的时候,也是我们经常要做的操作:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| a = np.arange(12).reshape(3,4)
print (f'原数组:\n{a}')
print (f'\n 对换数组:\n{np.transpose(a)}')
---
原数组:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
对换数组:
[[ 0 4 8]
[ 1 5 9]
[ 2 6 10]
[ 3 7 11]]
|
让我们再来看一种处理方式,与transpose方法一致:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| a = np.arange(12).reshape(3,4)
print (f'原数组:\n{a}')
print (f'\n 转置数组:\n{a.T}')
---
原数组:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
转置数组:
[[ 0 4 8]
[ 1 5 9]
[ 2 6 10]
[ 3 7 11]]
|
接着我们尝试一个函数用于交换数组的两个轴
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| t1 = np.arange(24).reshape(4,6)
re = t1.swapaxes(1,0)
print (f'\n 原数组:\n{t1}')
print (f'\n 调用 swapaxes 函数后的数组:\n{re}')
---
原数组:
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]
[12 13 14 15 16 17]
[18 19 20 21 22 23]]
调用 swapaxes 函数后的数组:
[[ 0 6 12 18]
[ 1 7 13 19]
[ 2 8 14 20]
[ 3 9 15 21]
[ 4 10 16 22]
[ 5 11 17 23]]
|
这几种方式都完成了转置操作,平时工作中,我们可以都尝试一下。
总结
最后,我们还是对 NumPy 整个的做一个总结:

然后,让我们留点作业吧:
- 练习矩阵相乘
- 练习数组索引
- 练习数组形状修改
大家要好好的完成作业。那本节课就到这里了,下课。







