26. 深度学习进阶 - 深度学习的优化方法

Hi, 你好。我是茶桁。

上一节课中我们预告了，本节课是一个难点，同时也是一个重点，大家要理解清楚。

我们在做机器学习的时候，会用不同的优化方法。

SGD

上图中左边就是 Batch Gradient Descent，中间是 Mini-Batch Gradient Descent, 最右边则是 Stochastic Gradient Descent。

我们还是直接上代码写一下来看。首先我们先定义两个随机值，一个 x，一个 ytrue：

import numpy as np
x = np.random.random(size=(100, 8))
ytrue = torch.from_numpy(np.random.uniform(0, 5, size=(100, 1)))

x 是一个 1008 的随机值，ytrue 是 1001 的随机值，在 0 到 5 之间，这 100 个 x 对应着这 100 个 ytrue 的输入。

然后我们来定义一个 Sequential, 在里面按顺序放一个线性函数，一个 Sigmoid 激活函数，然后再来一个线性函数，别忘了咱们上节课所讲的，要注意 x 的维度大小。

linear = torch.nn.Linear(in_features=8, out_features=1)
sigmoid = torch.nn.Sigmoid()
linear2 = torch.nn.Linear(in_features=1, out_features=1)

train_x = torch.from_numpy(x)

model = torch.nn.Sequential(linear, sigmoid, linear2).double()

我们先来看一下训练 x 和 ytrue 值的大小：

print(model(train_x).shape)
print(ytrue.shape)

---
torch.Size([100, 1])
torch.Size([100, 1])

然后我们就可以来求 loss 了，先拿到预测值，然后将预测值和真实值一起放进去求值。

loss_fn = torch.nn.MSELoss()
yhat = model(train_x)
loss = loss_fn(yhat, ytrue)
print(loss)

---
36.4703

我们现在可以定义一个 optimer， 来尝试进行优化，我们来将之前的所做的循环个 100 次，在其中我们加上反向传播：

optimer = torch.optim.SGD(model.parameters(), lr=1e-3)

for e in range(100):
    yhat = model(train_x)
    loss = loss_fn(yhat, ytrue)
    loss.backward()
    print(loss)
    optimer.step()

---
tensor(194.9302, dtype=torch.float64, grad_fn=<MseLossBackward0>)
...
tensor(1.9384, dtype=torch.float64, grad_fn=<MseLossBackward0>)

可以看到，loss 会一直降低。从 194 一直降低到了 2 左右。

在求解 loss 的时候，我们用到了所有的train_x，那这种方式就叫做 Batch gradient Descent，批量梯度下降。

它会对整个数据集计算损失函数相对于模型参数的梯度。梯度是一个矢量，包含了每个参数相对与损失函数的变化率。

这个方法会使用计算得到的梯度来更新模型的参数。更新规则通常是按照一下方式进行：

\[ \begin{align*} w_{t+1} = w_t - \eta \triangledown w_t \end{align*} \]

\(w_{t+1}\)是模型参数，\(\eta\)是学习率， \(\triangledown w_t\)是损失函数相对于参数的梯度。

但是在实际的情况下这个方法可能会有一个问题，比如说，我们在随机 x 的时候参数不是 100，而是 10^8，维度还是 8 维。假如它的维度很大，那么会出现的情况就是把 x 给加载到模型里面运算的时候，消耗的内存就会非常非常大，所需要的运算空间就非常大。

这也就是这个方法的一个缺点，计算成本非常高，由于需要计算整个训练数据集的梯度，因此在大规模数据集上的计算成本较高。而且可能会卡在局部最小值，难以逃离。说实话，我上面演示的数据也是尝试了几次之后拿到一次满意的，也遇到了在底部震荡的情况。

在这里可以有一个很简单的方法，我们规定每次就取 20 个:

for e in range(100):
    for b in range(100 // 20):
        batch_index = np.random.choice(range(len(train_x)), size=20)

        yhat = model(train_x[batch_index])
        loss = loss_fn(yhat, ytrue[batch_index])
        loss.backward()
        print(loss)
        optimer.step()

这样做 loss 也是可以下降的，那这种方法就叫做 Mini Batch。

还有一种方法很极端，就是 Stochhastic Gradient Descent，就是每次只取一个个数字:

for e in range(100):
    for b in range(100 // 1):
        ...

这种方法很极端，但是可以每次都可以运行下去。那大家就知道，有这三种不同的优化方式。

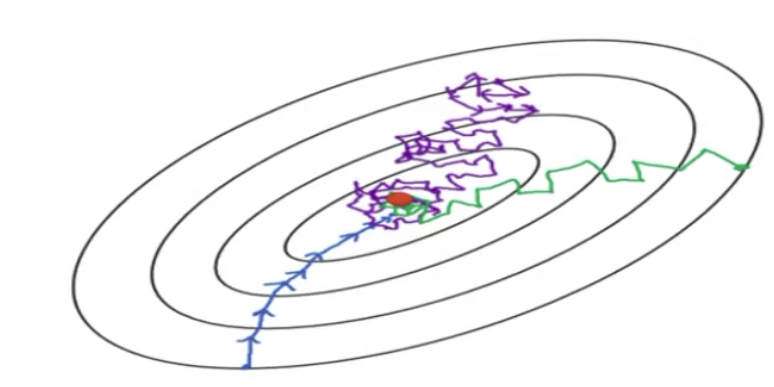
这样的话，我们来看一下，上图中的蓝色，绿色和紫色，分别对应哪种训练方式？

紫色的是 Stochastic Gradient Descent，因为它每次只取一个点，所以它的 loss 变化会很大，随机性会很强。换句话说，这一次取得数据好，可能 loss 会下降，如果数据取得不好，它的这个抖动会很大。

绿色就是 Mini-Batch, 我们刚才 20 个、20 个的输入进去，是有的时候涨，有的时候下降。

最后蓝色的就是 Batch Gradient Descent， 因为它 x 最多，所以下降的最稳定。

但是因为每次 x 特别多内存，那有可能就满了。内存如果满了，机器就没有时间去运行程序，就会变得特别的慢。

MOMENTUM

我们上面讲到的了这个式子：

\[ \begin{align*} w_{t+1} = w_t - \eta \triangledown w_t \end{align*} \]

这个是最原始的 Grady descent, 我们会发现一个问题，就是本来在等高线上进行梯度下降的时候，它找到的不是最快的下降的那条线，在实际情况中，数据量会很多，数量会很大。比方说做图片什么的，动辄几兆几十兆，如果要再加载几百个这个进去，那就会很慢。这个梯度往往可能会变的抖动会很大。

那有人就想了一个办法去减少抖动。就是我们每一次在计算梯度下降方向的时候，连带着上一次的方向一起考虑，然后取一个比例改变了原本的方向。那这样的话，整个梯度下降的线就会平缓了，抖动也就没有那么大，这个就叫做 Momentum, 动量。

\[ \begin{align*} v_t & = \gamma \cdot v_{t-1} + \eta \triangledown w_t \\ w_{t+1} & = w_t - v_t \end{align*} \]

动量在物理学中就是物体沿某个方向运动的能量。

之前我们每次的 wt 是直接去减去学习率乘以梯度，现在还考虑了 v{t-1}的值，乘上一个 gamma，这个值就是我们刚才说的取了一个比例。

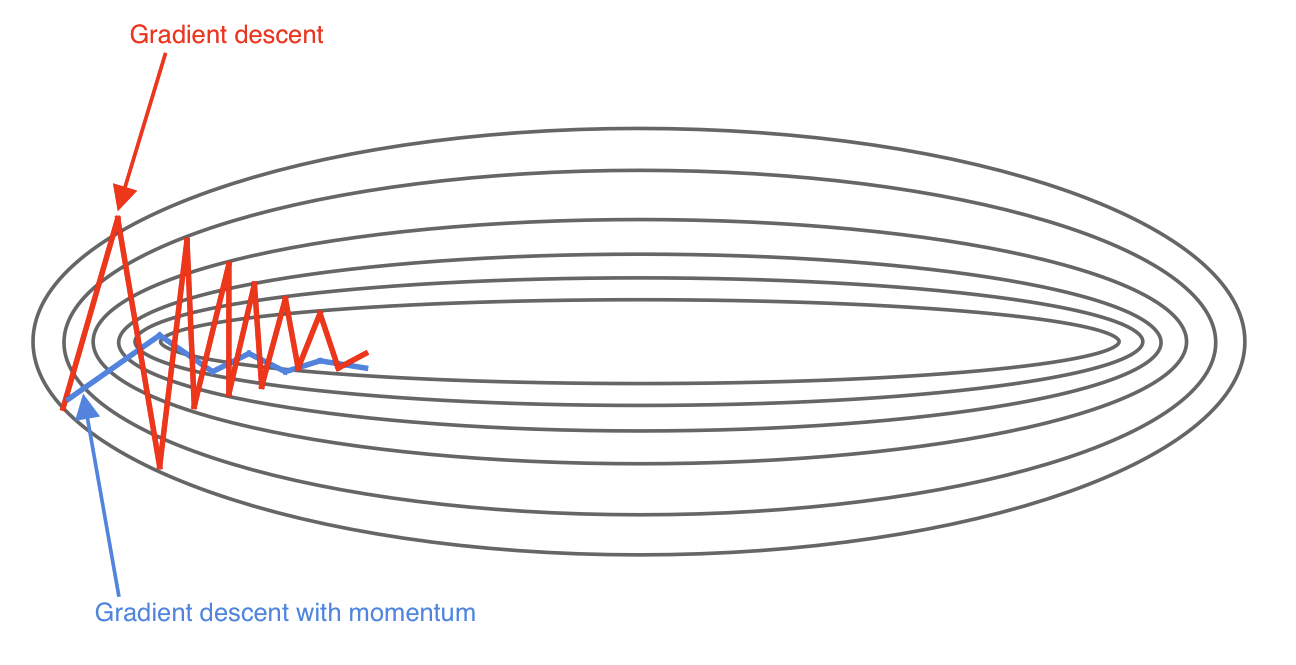
就像这个图一样，原来是红色，加了动量之后就变成蓝色，可以看到更平稳一些。

RMS-PROP

除了动量法之外呢，还有一个 RMS-PROP 方法，全称为 Root mean square prop。

\[ \begin{align*} S_{\frac{\partial loss}{\partial w}} & = \beta S_{\frac{\partial loss}{\partial w}} + (1 - \beta)||\frac{\partial loss}{\partial w} ||^2 \\ S_{\frac{\partial loss}{\partial b}} & = \beta S_{\frac{\partial loss}{\partial b}} + (1 - \beta)||\frac{\partial loss}{\partial b} ||^2 \\ w & = w - \alpha \frac{\frac{\partial loss}{\partial w}}{\sqrt{S_{\frac{\partial loss}{\partial w}}}} \\ b & = b - \alpha \frac{\frac{\partial loss}{\partial b}}{\sqrt{S_{\frac{\partial loss}{\partial b}}}} \end{align*} \]

这个方法看似复杂，其实也是非常简单。这些方法在 PyTorch 里其实都有包含，我们可以直接调用。我们在这里还是要理解一下它的原理，之后做事的时候也并不需要真的取从头写这些玩意。

在讲它之前，我们再回头来说一下刚刚求解的动量法，动量法其实已经做的比较好了，但是还是有一个问题，它每次的 rate 是人工定义的。也就是我们上述公式中的\(\gamma\), 这个比例是人工定义的，那在 RMS-PROP 中就写了一个动态的调整方法。

这个动态的调整方法就是我们每一次在进行调整 w 或者 b 的时候，都会除以一个根号下的\(S_{\frac{\partial loss}{\partial w}}\)，我们往上看，如果\(\frac{\partial loss}{\partial w}\)比较大的话，那么\(S_{\frac{\partial loss}{\partial w}}\)也就将会比较大，那放在下面的式子中，根号下，也就是\(\sqrt{S_{\frac{\partial loss}{\partial w}}}\)在分母上，那么 w 就会更小，反之则会更大。

所以说，当这一次的梯度很大的时候，这样一个方法就让\(\frac{\partial loss}{\partial w}\)其实变小了，对 b 来说也是一样的情况。

也就说，如果上一次的方向变化的很严重，那么这一次就会稍微的收敛一点，就会动态的有个缩放。那么如果上一次变化的很小，那为了加速它，这个值反而就会变大一些。

所以说他是实现了一个动态的学习率的变化，当然它前面还有一个初始值，这个\(\gamma\)需要人为设置，但是在这个\(\gamma\)基础上它实现了动态的学习速率的变化。

动态的学习速率考察两个值，一个是前一时刻的变化的快慢，另一个就是它此时此刻变化的快慢。这个就叫做 RMS。

ADAM

那我们在这里，其实还有一个方法：ADAM。 \[ \begin{align*} V_{dw} & = \beta_1V_{dw} + (1-\beta_1)dw \\ V_{db} & = \beta_1V_{db} + (1-\beta_1)db \\ S_{dw} & = \beta_2S_{dw} + (1-\beta_2)||dw||^2 \\ S_{db} & = \beta_2S_{db} + (1-\beta_2)||db||^2 \\ & V_{dw}^{corrected} = \frac{V_{dw}}{1-\beta_1^t} \\ & V_{db}^{corrected} = \frac{V_{db}}{1-\beta_1^t} \\ & S_{dw}^{corrected} = \frac{S_{dw}}{1-\beta_2^t} \\ & S_{db}^{corrected} = \frac{S_{db}}{1-\beta_2^t} \\ w & = w - \alpha\frac{V_{db}^{corrected}}{\sqrt{S_{dw}^{corrected}}+\varepsilon} \\ b & = b - \alpha\frac{V_{db}^{corrected}}{\sqrt{S_{db}^{corrected}}+\varepsilon} \\ \end{align*} \]

刚刚讲过的 RMS 特点其实是动态的调整了我们的学习率，之前讲 Momentum 其实还保持了上一时刻的方向，RMS 就没有解决这个问题，RMS 把上一时刻的方向给弄没了。

RMS，它的定义其实就没有考虑上次的方向，它只考虑上次变化的大小。而现在提出来这个 ADAM，这个 ADAM 的意思就是 Adaptive Momentum, 还记不记得咱们讲随机森林和 Adaboost 那一节，我们讲过 Adaboost 就是 Adaptive Boosting，这里的 Adaptive 其实就是一个意思，就是自适应动量，也叫动态变化动量。

ADAM 就结合了 RMS 和动量的两个优点。第一个是他在分母上也加了一个根号下的数，也就做了 RMS 做的事，然后在分子上还有一个数，这个数就保留了上一时刻的数，比如\(V_{dw}^{corrected}\)， 就保留了上一时刻的 V，就保留了上一时刻的方向。

所以 ADAM 既是动态的调整了学习率，又保留了上一时刻的方向。

那除此之外，其实还有一个 AdaGrad 和 L-BFGS 方法，不过常用的方法也就是上面详细讲的这几种。

到此为止，我们进阶神经网络的基础知识就都差不多具备了，接下来我们就该来讲解下卷机和序列，比如说 LSTM 和 RNN、CNN 的东西。在这些结束之后，我们还会有 Attention 机制，Transformer 机制，YOLO 机制，Segmentation 机制，还有强化深度学习其实都是基于这些东西。

那我们下节课，就先从 RNN 来说开去。