28. 深度学习进阶 - LSTM

Hi, 你好。我是茶桁。

我们上一节课，用了一个示例来展示了一下我们为什么要用 RNN 神经网络，它和全连接的神经网络具体有什么区别。

这节课，我们就着上一节课的内容继续往后讲，没看过上节课的，建议回头去好好看看，特别是对代码的进程顺序好好的弄清楚。

全连接的模型得很仔细的去改变它的结构，然后再给它加很多东西，效果才能变好：

self.linear_with_tanh = nn.Sequential(
    nn.Linear(10, self.hidden_size),
    nn.Tanh(),
    nn.Linear(self.hidden_size, self.hidden_size),
    nn.Tanh(),
    nn.Linear(self.hidden_size, output_size)
)

但是对于 RNN 模型来说，我们只用了两个函数：

self.rnn = nn.RNN(x_size, hidden_size, n_layers, batch_first=True)
self.out = nn.Linear(hidden_size, output_size) 

这是一个很本质的问题, 也比较重要。为什么 RNN 的模型这么简单，它的效果比更复杂的全连接要好呢？

这个和我们平时生活中做各种事情其实都很类似，他背后的原因是他的信息保留的更多。RNN 模型厉害的本质是在运行的过程中把更多的信息记录下来，而全连接没有记录。

对于 RNN 模型，还有两个点大家需要注意。

第一个，有一种叫做 stacked 的 RNN 的模型。我们 RNN 模型每一次输出都有一个 output 和 hidden，把 outputs 和 hidden 作为它的输入再传给另外一个 RNN 模型，模型就变得更复杂，理论上可以解决些更复杂的场景。我们把这种就叫做 stacked RNN。

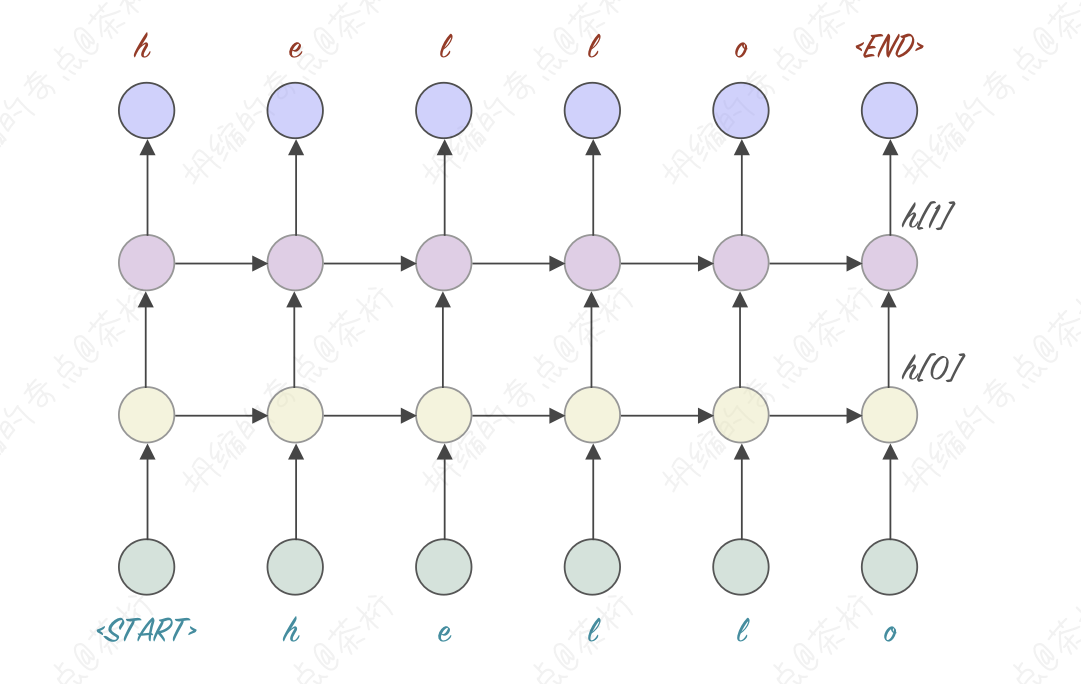
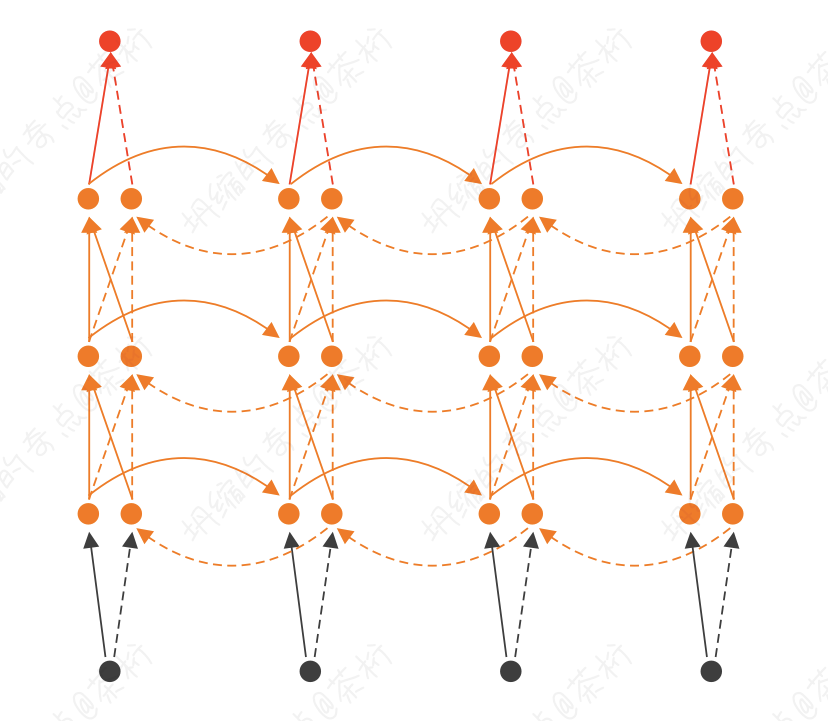
还有一种形式，Bidirectional RNN，双向 RNN。有一个很著名的文本模型 Bert, 那个 B 就是双向的意思。

我们回过头来看上节课我们讲过的两种网络：

\[ \begin{align*} h_t & = \sigma_h(W_hx_t + U_hh_{t-1} + b_h) \\ y_t & = \sigma_y(W_yh_t + b_y) \end{align*} \]

在这个里面，每一时刻的 y_t 只和 y_{t-1} 有关系，如果把所有的 x 一次性给到模型的时候，其实我们在这里可以给它加一个东西：

\[ \begin{align*} h_t & = \sigma_h(W_hx_t + U_hh_{t-1} + V_h * h_{t+1} + b_h) \end{align*} \]

还可以写成这样，那这样的话它实现的就是每一时刻的 t 既和前一次有关系 和后一刻有关系。这样我们每一次的值不仅和前面有关，还和后面有关。就叫做双向 RNN。

对于 RNN 来说，它有一个很严重的问题，就是之前说过的，它的 vanishing 和 exploding 的问题会很明显, 也就是梯度消失和爆炸问题。

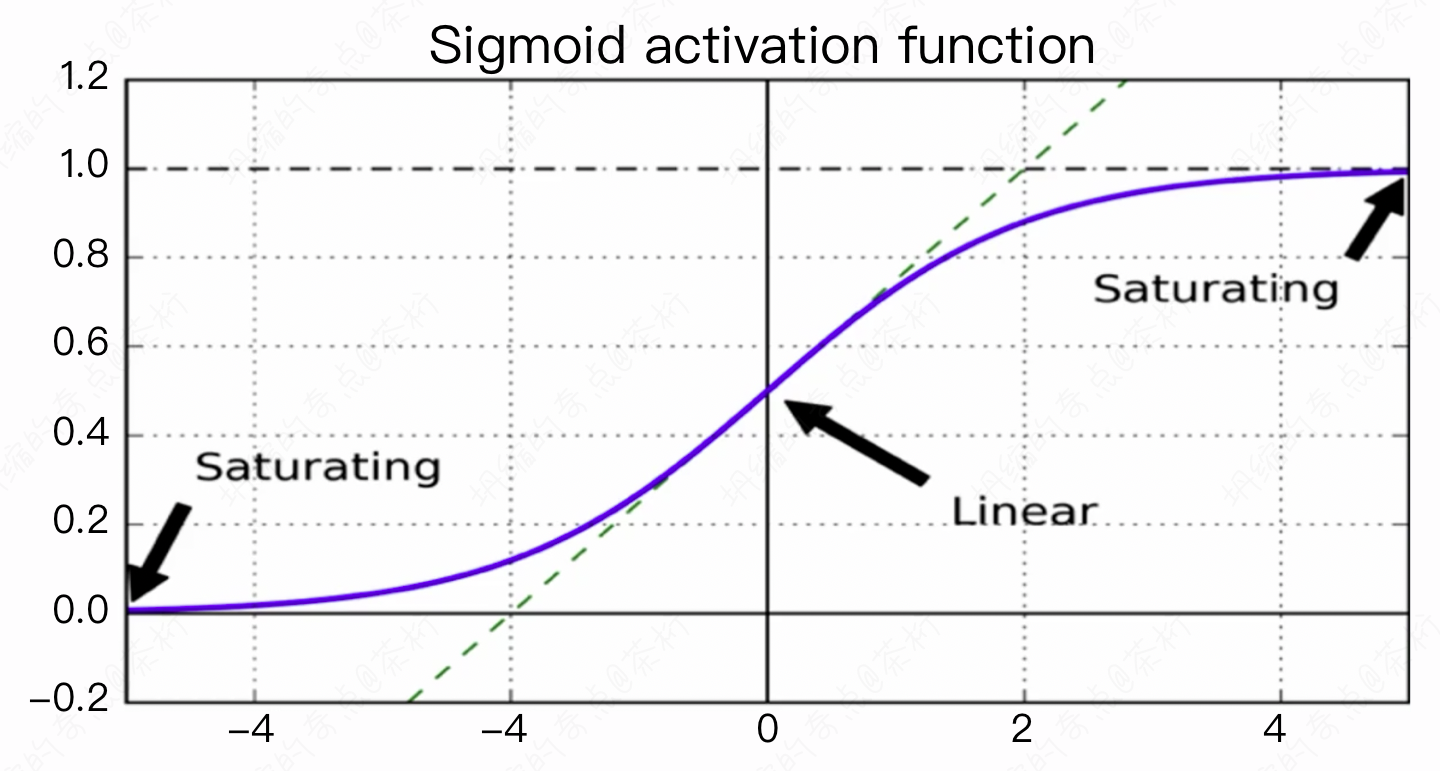
想一下，现在如果有一个 loss，那它最终的 loss 是不是对于{x1, x2, ..., xn}都有关系，比方说现在要求\(\frac{\partial loss}{\partial w_1}\), 假如说现在 h 是 100， 那这种调用关系就是

\[ \begin{align*} \frac{\partial loss}{\partial w_1} = \frac{\partial h_{100}}{\partial h_{99}} \cdot \frac{\partial h_{99}}{\partial h_{98}} \cdot ... \cdot \frac{\partial h_{0}}{\partial w_{1}} \end{align*} \]

loss 对于 w1 求偏导的时候，其实 loss 最先接受的是离他最近的, 假如说是 h100。h100 调用了 h99,h99 调用 h98，就这个调用过程，这一串东西会变得很长。

我们之前课程说过一些情况，怎么去解决这个问题呢？对于 RNN 模型来说梯度爆炸很好解决，就直接设定一个阈值就可以了，起码也是能学习的。

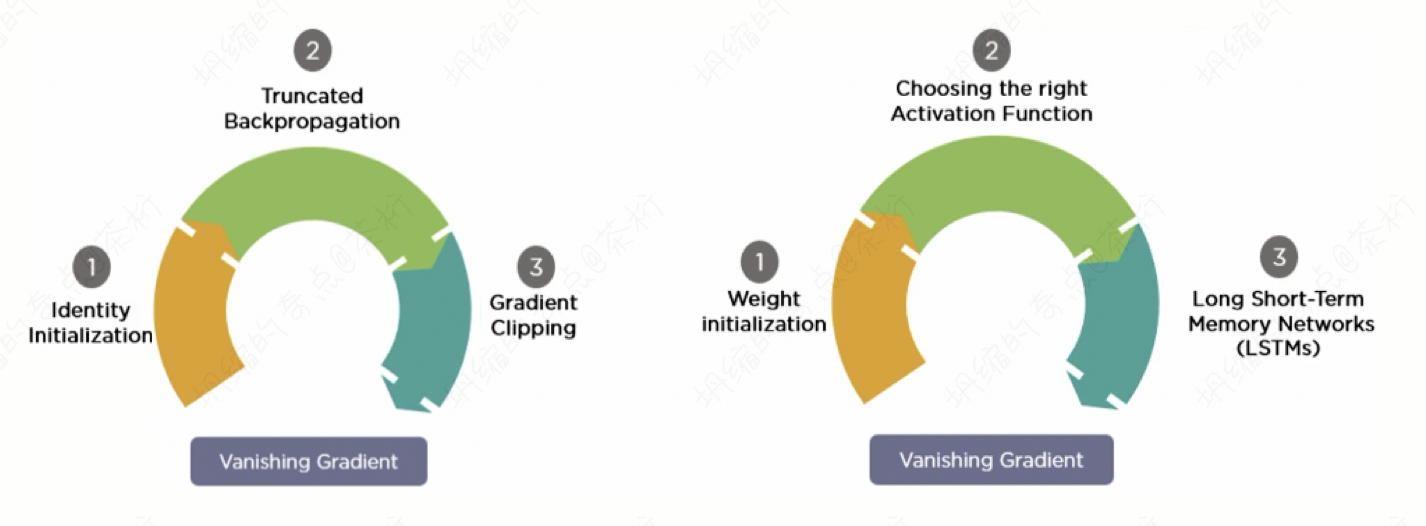
要讲的是想一种方法怎么样来解决梯度消失的问题。这个梯度消失的解决方法，就叫 LSTM。要解决梯度消失，就是要用 LSTM: Long Short-Term Memory，长短记忆模型，既能保持长信息，又能保持短信息。

在之前那个很长的过程中，怎么样能够让它不消散呢？LSTM 的核心思想是通过门控机制来控制信息的流动和及已的更新，包含了 Input Gate, Forget Gate，Cell State 以及 Output Gate。这些会一起协作来处理序列数据。

其中 Input Gate 控制着新信息的输入，以及信息对细胞状态的影响。 Forget Gate 控制着细胞状态中哪些信息应该被易王，Cell State 用于传递信息，是 LSTM 的核心，Output Gate 控制着细胞状态如何影响输出。

这里每一个门控单元都由一个 Sigmoid 激活函数来控制信息的流动，以及一个 Tanh 激活函数来确定信息的值。

\[ \begin{align*} Input Gate \\ i_t & = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i) \\ C't & = \tanh(W_c \cdot [h{t-1}, x_t] + b_c) \\ C_t & = f_t \cdot C_{t-1} + i_t \cdot C'_t \\ Forget Gate \\ f_t & = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f) \\ C_t & = f_t \cdot C_{t-1} + i_t \cdot C'_t \\ Output Gate \\ o_t & = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o) \\ h_t & = o_t \cdot \tanh(C_t) \end{align*} \]

其中，\(h_{t-1}\) 是前一个时间步的隐藏状态，\(x_t\) 是当前时间步的输入，\(W_i, W_f, W_o, W_c\) 是权重矩阵，\(b_i, b_f, b_o, b_c\) 是偏置。

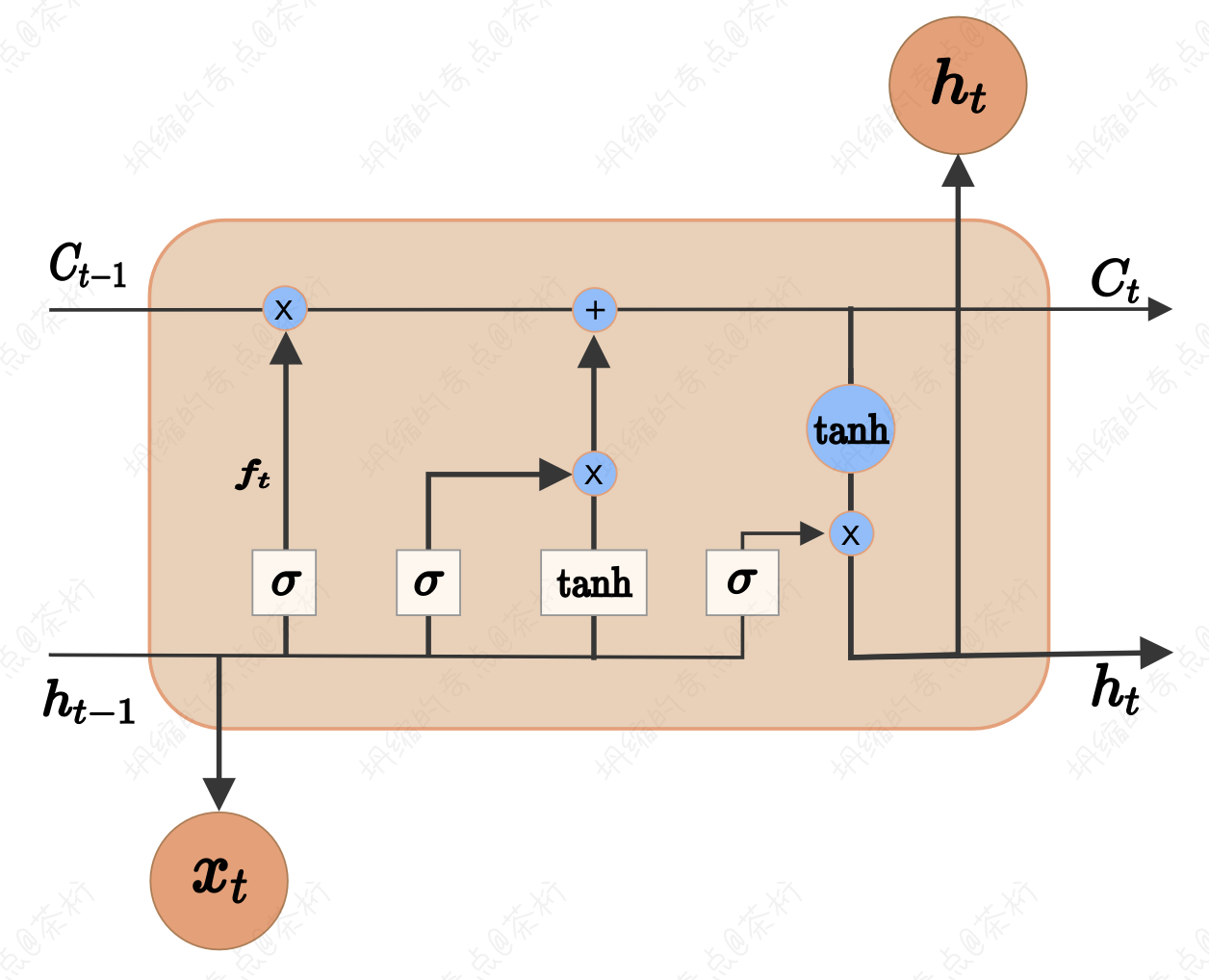
LSTM 输入的是一个序列数据，可以是文本、时间序列，音频信号等等。那每个时间步的输入是序列中的饿一个元素，比如一个单词、一个时间点的观测值等等。

假设我们有一个序列 x = [x1, x2, ..., xt]， 其中 t 就代表的是时间步。

xt 进来的时候, 之前我们是只接收一个 hidden state, 现在我们多接收了一个\(C_{t-1}\)，这个就是我们的 Cell，这一步的\(C_{t-1}\)其实就是上一步的\(C_t\)。

在训练开始时，需要初始化 LSTM 单元的隐藏状态 h0 和细胞状态 c0。通常我们初始化它们为全零向量。

最开始的时候，我们要进入 Input Gate, 对于每个时间步 t, 计算输入门的激活值\(i_t\)，控制新信息的输入。使用 Sigmoid 函数来计算输入门的值：

\[ i_t = \sigma (W_i \cdot [h_{t-1}, x_t] + b_i) \]

然后，计算新的侯选值\(C'_t\)， 这是在当前时间步考虑的新信息。使用 tanh 激活函数来计算侯选值：

\[ C'_t = tanh(W_c \cdot [h_{t-1}, x_t] + b_c) \]

接下来我们就要更新细胞状态了，细胞状态\(C_t\)更新是通过遗忘门\(f_t\)和输入门\(i_t\)控制的。遗忘门控制着哪些信息应该被遗忘，输入门控制新信息对细胞状态的影响：

\[ C_t = f_t \cdot C_{t-1} + i_t \cdot C'_t \]

那遗忘门决定哪些信息应该被遗忘，使用的就是 Sigmoid 函数计算遗忘门的激活值。

\[ f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f) \]

接着，计算输出门\(O_t\), 控制着细胞状态如何影响输出和隐藏状态。一样，我们还是使用 Sigmoid 函数计算。

\[ o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o) \]

使用输出门的值\(o_t\)来计算最终的隐藏状态\(h_t\)和输出。 隐藏状态和输出都是根据细胞状态和输出门的值来计算的：

\[ h_t = o_t \cdot tanh(C_t) \]

接下来就容易了，我们迭代重复上述过程，处理序列中的每一个时间步，直到处理完整个序列。

LSTM 的输出可以是隐藏状态\(h_t\), 也可以是细胞状态\(C_t\)， 具体是取决于应用的需求。

后来大家就发现了一种改进的 LSTM，其中门控机制允许细胞状态窥视现前的细胞状态的信息，而不仅仅是根据当前时间步的输入和隐藏状态来决定。 这个机制在 LSTM 单源种引入了额外的权重和连接，以允许细胞状态在门控过程中访问现前的细胞状态，我们称之为窥视孔连接: Peephole connections。

\[ \begin{align*} f_t = \sigma(W_f \cdot [C_{t-1}, h_{t-1}, x_t] + b_f) \\ i_t = \sigma(W_i \cdot [C_{t-1}, h_{t-1}, x_t] + b_i) \\ o_t = \sigma(W_o \cdot [C_{t-1}, h_{t-1}, x_t] + b_o) \\ \end{align*} \]

之前，我们是 xt 和 x_{t-1}决定的 f，那现在又把 c_{t-1}加上了。就是多加了一些信息。

除此之外它有一个方法 GRU，这个是 2014 年提出来的，Geted Recurrent Unit，它是 LSTM 的一个简化版本。

它最核心的内容：

\[ \begin{align*} h_t = (1-z_t) \cdot h_{t-1} + z_t \cdot h'_t \end{align*} \]

咱们刚刚是\(C_t = f_t \cdot C_{t-1} + i_t \cdot C'_t\)，也就是遗忘加上输入，那我们对过去保留越多的时候， 输入就会越小，那对过去保留越小的时候，输入就会越大。

所以既然 f 也是 1-0，i 也是 0-1，f 大的时候 i 就小，f 小的时候 i 就大，那么能不能写成 f=(1-i)？

于是，GRU 就这样实现了, 它其实最核心的就做了这样一件事， f=(1-i)。

\[ \begin{align*} z_t & = \sigma(W_z \cdot [h_{t-1}, x_t]) \\ r_t & = \sigma(W_r \cdot [h_{t-1}, x_t]) \\ h'_t & = \tanh(W \cdot [r_t \cdot h_{t-1}, x_t]) \\ h_t & = (1-z_t) \cdot h_{t-1} + z_t \cdot h'_t \end{align*} \]

这个 z 其实和 i 是一样的东西，只是原作者为了发表论文方便而改了个名称。

https://arxiv.org/pdf/1406.1078v3.pdf

\(r_t\)是来控制上一时刻的\(h_t\)在我们此时此刻的重要性、影响程度。那我们可以将\(r_t \cdot h_{t-1}\)看成是关于及已的，\(1-z_t\)也是关于记忆的。

GRU 这样做之后有什么好处呢?

原来我们有三个门: f, i, o， 那现在变成了两个，z 和 r。为什么就更好了呢？我们在 PyTorch 里面往往用的是 GRU。

大家想一下，是不是少了一个门其实就少了一个矩阵？我们看公式的时候，\(W_f\)是一个数学符号，但是在背后其实是一个矩阵，是一个矩阵的话少了一个矩阵意味着参数就少多了，运算就更快了等等。

但其实这些都不是最关键的，最关键的是减少过拟合了。我们之前的课程中一再强调，过拟合之所以产生，最主要的原因是数据不够或者说是模型太复杂。

但是在现有的数据情况下，为了让数据发挥出最大效力，你把需要训练的模型变简单，参数变少，就没有那么复杂了。

关于 RNN 模型，我们后面还会介绍一些具体的示例。